Benda yang bergerak lurus beraturan memiliki kecepatan yang tetap (konstan), sehingga nilai percepatannya adalah nol.
$$\bbox[yellow, 5pt]{s = s_0 + v\cdot t}$$
Keterangan:
- \(s = \text{ posisi akhir}\)
- \(s_0 = \text{ posisi awal}\)
- \(v = \text{ kecepatan}\)
- \(t = \text{ waktu}\)
Grafik kecepatan v.s waktu
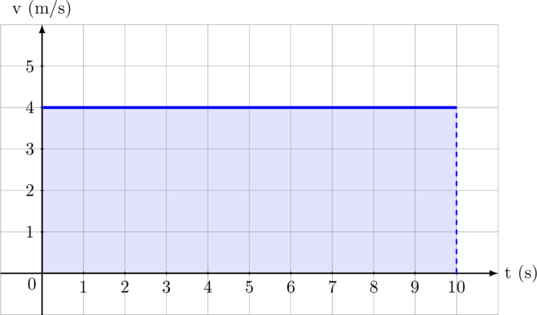
Grafik di atas menunjukkan sebuah benda yang bergerak dengan kecepatan tetap 4 m/s selama 10 sekon.
Jarak yang ditempuh sama dengan luas daerah yang diarsir.
Jarak yang ditempuh = luas persegi panjang
Jarak yang ditempuh = 10 × 4 = 40 m
Grafik jarak v.s waktu
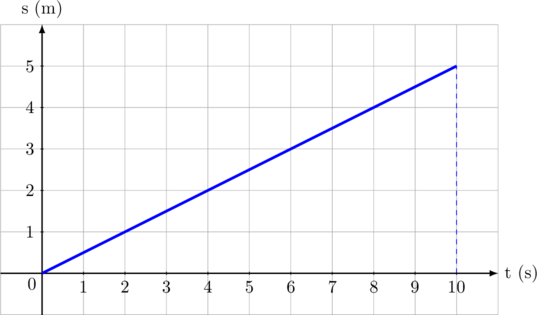
Grafik di atas menunjukkan sebuah benda bergerak lurus beraturan, selama waktu 10 sekon telah menempuh jarak 5 m. Kemiringan garis (gradien) menunjukan besar kecepatan tetapnya.
\(\text{Gradien garis } = \dfrac{\triangle y}{\triangle x}\)
\(\text{Gradien garis } = \dfrac{5 – 0}{10-0} = \dfrac{1}{2}\)
Jadi besar kecepatannya adalah \(\dfrac{1}{2}\) m/s.
Contoh Soal
Sebuah mobil melaju di jalan tol yang lurus dengan kecepatan tetap 72 km/jam. Berapa jarak yang sudah ditempuh selama perjalanan 30 menit?
Diketahui:
\(v = 72 \text{ km/jam} = \dfrac{72000 \text{ m}}{3600 \text{ s}} = 20 \text{ m/s}\)
\(t = 30 \text{ menit} = 30 \times 60 \text{ s} = 1800 \text{ s}\)
Ditanyakan: s?
Penyelesaian:
\(s = s_0 + v\cdot t\)
\(s = 0 + 20\cdot 1800\)
\(s = 36000 \text{ m}\:\:\:\:\:\color{blue} 1 \text{ km} = 1000 \text{ m}\)
\(s = 36 \text{ km}\)
Jadi jarak yang sudah ditempuh 36 km
Sebuah kereta api bergerak lurus beraturan dengan kecepatan tetap 108 km/jam, kereta api tersebut melewati tempat A pada pukul 06:00 pagi selanjutnya melewati tempat B pada pukul 07:15 pagi. Berapa jarak antara tempat A dan tempat B?
Diketahui:
\(v = 108 \text{ km/jam} = \dfrac{108000 \text{ m}}{3600 \text{ s}} = 30 \text{ m/s}\)
\(t = 07:15\: -\: 06:00 = 75 \text{ menit}\)
\(t = 75 \times 60 \text{ s}\)
\(t = 4500 \text{ s}\)
Ditanyakan: s?
Penyelesaian:
\(s = s_0 + v\cdot t\)
\(s = 0 + 30\cdot 4500\)
\(s = 135000 \text{ m}\:\:\:\:\:\color{blue} 1 \text{ km} = 1000 \text{ m}\)
\(s = 135 \text{ km}\)
Jadi jarak antara tempat A dan tempat B adalah 135 km
Sebuah mobil ambulance melewati pos polisi dengan kecepatan tetap 90 km/jam, 1 menit kemudian seorang pemotor melewati pos polisi yang sama dengan kecepatan tetap 108 km/jam searah dengan mobil ambulance tadi. Pada jarak berapa pemotor dapat menyusul mobil ambulance jika diukur dari pos polisi?
Diketahui:
\(v_1 \text{ kecepatan ambulance}\)
\(v_1 = 90 \text{ km/jam}\)
\(v_1 = 25 \text{ m/s}\)
\(v_2 \text{ kecepatan motor}\)
\(v_2 = 108 \text{ km/jam}\)
\(v_2 = 30 \text{ m/s}\)
\(t_1 = t_2 + 60 \text{ s}\)
Mobil ambulance bergerak 1 menit (60 sekon) lebih dahulu dari motor
Ditanyakan: posisi pemotor saat menyusul ambulance diukur dari pos polisi?
Penyelesaian:
Pada saat pemotor dapat menyusul mobil ambulance posisi akhir pemotor dan ambulance adalah sama jika diukur dari pos polisi (posisi awal)
\(s_{\text{ambulance}} = s_{\text{motor}}\)
\(s_0 + v_1\cdot t_1 = s_0 + v_2\cdot t_2\)
Masukkan posisi awal mobil dan motor = nol, karena acuan geraknya adalah pos polisi
\(0 + 25\cdot t_1 = 0 + 30\cdot t_2\)
Kemudian substitusikan \(t_1 = t_2 + 60 \text{ s}\)
\(25(t_2 + 60) = 30t_2\)
\(25t_2 + 1500 = 30t_2\)
\(1500 = 30t_2 – 25t_2\)
\(1500 = 5t_2\)
\(t_2 = \dfrac{1500}{5} = 300 \text{ s}\)
300 detik adalah waktu pemotor dapat menyusul mobil ambulance
Kemudian substitusikan \(t_2 = 300 \text{ s}\) ke persamaan \(s_{\text{ motor}}\)
\(s_{\text{ motor}} = s_0 + v_2\cdot t_2\)
\(s_{\text{ motor}} = 0 + 30\cdot 300\)
\(s_{\text{ motor}} = 9000 \text{ m} = 9 \text{ km}\)
Jadi pemotor dapat menyusul ambulance pada jarak 9 km diukur dari pos polisi
Seorang pemotor bergerak lurus pada lajur kiri jalan dengan kecepatan tetap 40 km/jam melewati tempat A. Dari arah yang berlawanan datang mobil ambulance dengan kecepatan tetap 80 km/jam melewati tempat B di lajur sebelah kanan. Jika jarak antara tempat A dan B adalah 2 km, tentukan posisi pemotor saat berpapasan dengan mobil ambulance diukur dari tempat A.
Diketahui:
\(v_1 \text{ kecepatan pemotor}\)
\(v_1 = +40 \text{ km/jam}\)
\(\color{blue}\text{arah ke kanan}\)
\(v_2 \text{ kecepatan ambulance}\)
\(v_2 = -80 \text{ km/jam}\)
\(\color{blue}\text{arah ke kiri}\)
Note: anggap pemotor bergerak ke kanan, sedangkan mobil ambulance bergerak ke kiri
\(s_{\text{AB}} = 2 \text{ km}\)
Ditanyakan: posisi pemotor saat berpapasan dengan ambulance diukur dari tempat A?
Penyelesaian:
Pada saat pemotor berpapasan dengan mobil ambulance posisi akhir pemotor dan ambulance adalah sama jika diukur dari tempat A (posisi awal)
\(s_{\text{motor}} = s_{\text{ambulance}}\)
\(s_0 + v_1\cdot t_1 = s_0 + v_2\cdot t_2\)
Karena acuan geraknya adalah tempat A, maka posisi awal pemotor = nol, sedangkan posisi awal ambulance = 2 km
\(0 + 40\cdot t = 2 -80\cdot t\)
\(40t = 2 -80t\)
\(40t + 80t = 2\)
\(120t = 2\)
\(t = \dfrac{2}{120}\)
\(t = \dfrac{1}{60}\text{ jam}\)
\(\dfrac{1}{60}\text{ jam} = 1 \text{ menit}\) adalah waktu pemotor berpapasan dengan ambulance
Kemudian substitusikan \(t = \dfrac{1}{60}\text{ jam} \) ke persamaan \(s_{\text{ motor}}\)
\(s_{\text{ motor}} = s_0 + v_1\cdot t_1\)
\(s_{\text{ motor}} = 0 + 40\cdot \dfrac{1}{60}\)
\(s_{\text{ motor}} = \dfrac{40}{60} = \dfrac{2}{3}\text{ km}\)
jadi pemotor akan berpapasan dengan mobil ambulance pada jarak \(\dfrac{2}{3}\text{ km}\) diukur dari tempat A.
