Benda yang bergerak lurus berubah beraturan nilai percepatannya adalah tetap (konstan), sedangkan nilai kecepatannya berubah terhadap waktu.
$$\bbox[yellow, 5pt]{s = s_0 + v_0\cdot t + \dfrac{1}{2}\cdot a \cdot t^2}$$
$$\bbox[yellow, 5pt]{v_t = v_0 + a\cdot t}$$
$$\bbox[yellow, 5pt]{v_t ^2 = v_0 ^2 + 2a\cdot (s – s_0)}$$
Keterangan:
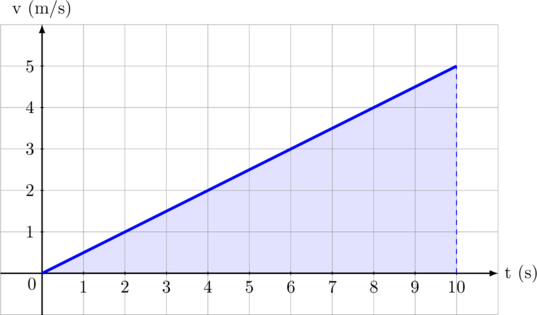
Grafik di atas menunjukkan gerak maju dipercepat secara beraturan, dari sebuah benda yang awalnya diam hingga mencapai kecepatan 5 m/s dalam waktu 10 sekon.
Gradien garis di atas menunjukkan nilai percepatan tetapnya.
Gradien garis = \(\dfrac{\triangle y}{\triangle x}\)
Gradien garis = \(\dfrac{5 – 0}{10 – 0} = \dfrac{1}{2}\)
Jadi nilai percepatannya adalah \(\dfrac{1}{2} \text{ m/s}^2\)
luas daerah yang diarsir menunjukkan jarak yang sudah ditempuh
Jarak yang ditempuh = luas segitiga
Jarak yang ditempuh = \(\dfrac{1}{2}\cdot \text{ alas} \cdot \text{ tinggi}\)
Jarak yang ditempuh = \(\dfrac{1}{2}\cdot 10 \cdot 5 = 25 \text{ m}\)
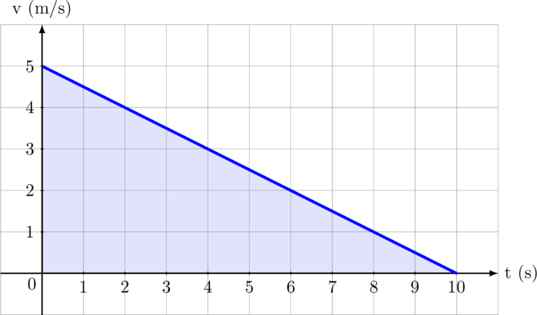
Grafik di atas menunjukkan gerak maju diperlambat secara beraturan, dari sebuah benda yang awalnya memiliki kecepatan 5 m/s hingga mencapai berhenti dalam waktu 10 sekon.
Gradien garis di atas menunjukkan nilai perlambatannya
Gradien garis = \(\dfrac{\triangle y}{\triangle x}\)
Gradien garis = \(\dfrac{0 – 5}{10 – 0} = -\dfrac{1}{2}\)
Jadi benda diperlambat sampai berhenti dengan nilai perlambatan \(\dfrac{1}{2}\text{ m/s}^2\)
luas daerah yang diarsir menunjukkan jarak yang ditempuh sampai benda tersebut berhenti
Jarak yang ditempuh = luas segitiga
Jarak yang ditempuh = \(\dfrac{1}{2}\cdot \text{ alas} \cdot \text{ tinggi}\)
Jarak yang ditempuh = \(\dfrac{1}{2}\cdot 10 \cdot 5 = 25 \text{ m}\)
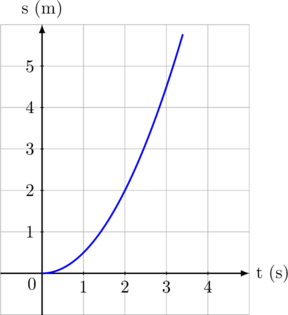
Grafik di atas menunjukkan gerak benda maju dipercepat secara beraturan (nilai percepatan positif)
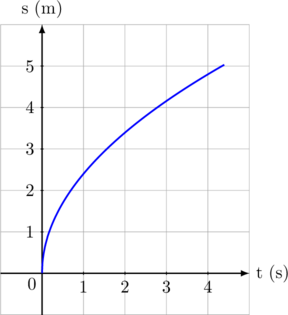
Grafik di atas menunjukkan gerak benda maju diperlambat secara beraturan (nilai percepatan negatif)
- \(s = \text{ posisi akhir}\)
- \(s_0 = \text{ posisi awal}\)
- \(v_t = \text{ kecepatan akhir}\)
- \(v_0 = \text{ kecepatan awal}\)
- \(a = \text{ percepatan}\)
- \(t = \text{ waktu}\)
Grafik antara kecepatan v.s waktu
Grafik antara jarak v.s waktu
Contoh Soal
Contoh 1
Sebuah partikel bergerak menurut grafik di bawah ini:
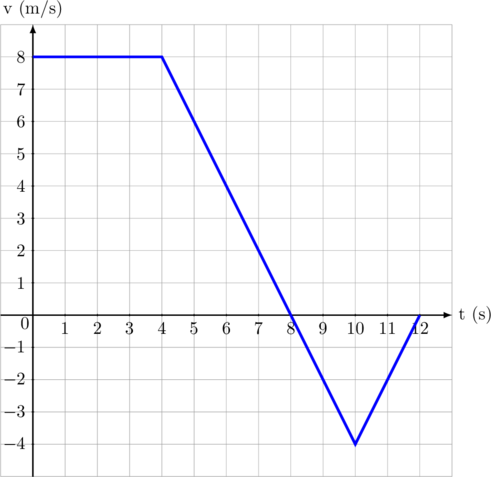
Tentukan:
a. Berikan analisa gerak partikel berdasarkan grafik di atas
b. Jarak total yang ditempuh partikel selama 12 detik bergerak
c. Perpindahan partikel selama 12 detik bergerak
Contoh 2
Grafik di bawah ini menunjukkan gerak partikel P dan partikel Q
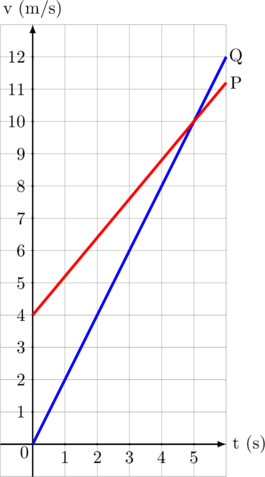
Jika kedua partikel bergerak dari tempat yang sama, maka tentukan:
a. Waktu yang diperlukan partikel Q untuk bisa menyusul partikel P
b. Jarak yang ditempuh partikel Q saat menyusul partikel P, diukur dari tempat awal mereka bergerak
