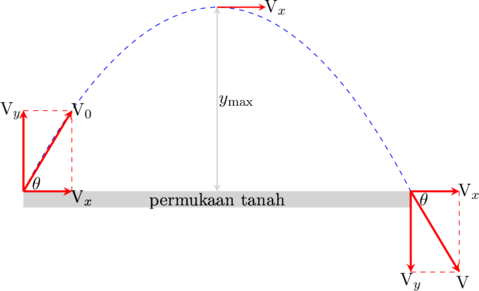
Analisa Gerak Parabola
Gerak Mendatar
Dalam arah mendatar kecepatan benda selalu konstan
\(\text{x} = \text{v}_{\text{x}}\cdot \text{t}\)
Keterangan:
\(\text{x} = \text{jangkauan}\)
\(\text{v}_{\text{x}} = \text{kecepatan arah sumbu x}\)
\(\text{t} = \text{waktu}\)
Gerak Vertikal
Gerak benda dalam arah vertikal dipengaruhi oleh percepatan gravitasi arah ke bawah yang konstan
\(\text{y} = \text{y}_{0} + \text{v}_{0\text{y}}\cdot \text{t} \:-\:\frac{1}{2}\cdot \text{g}\cdot \text{t}^2\)
\(\text{v}_{\text{y}} = \text{v}_{0\text{y}} \:-\:\text{g}\cdot \text{t}\)
Keterangan:
\(\text{y} = \text{ketinggian akhir}\)
\(\text{y}_{0} = \text{ketinggian awal}\)
\(\text{v}_{0\text{y}} = \text{kecepatan awal arah sumbu y}\)
\(\text{v}_{\text{y}} = \text{kecepatan arah sumbu y}\)
\(\text{g} = \text{percepatan gravitasi}\)
\(\text{t} = \text{waktu}\)
Menentukan Kecepatan
Komponen kecepatan awal
\(\text{v}_{0\text{x}} = \text{v}_{0}\cdot \cos \theta\)
\(\text{v}_{0\text{y}} = \text{v}_{0}\cdot \sin \theta\)
Kecepatan di suatu titik lintasan
Besar kecepatan di setiap titik lintasan merupakan resultan dari kecepatan arah sumbu-x dan kecepatan arah sumbu-y
\(\text{v} = \sqrt{(\text{v}_{\text{x}})^2 + (\text{v}_{\text{y}})^2}\)
Arah kecepatan:
\(\tan \theta = \dfrac{\text{v}_{\text{y}}}{\text{v}_{\text{x}}}\)
Pada titik tertinggi, \(\text{v}_{\text{y}} = 0\), sehingga besar kecepatan pada titik tertinggi sama dengan \(\text{v}_{\text{x}}\)
Rumus Singkat
Ketinggian maksimum
\(\text{y}_{\text{max}} = \dfrac{\text{v}_{0}^2\cdot \sin^2\theta}{2\text{g}}\)
Waktu sampai ketinggian maksimum
\(\text{t}_{\text{ymax}} = \dfrac{\text{v}_{0}\cdot \sin \theta}{\text{g}}\)
Jangkauan maksimum
\(\text{x}_{\text{max}} = \dfrac{\text{v}_{0}^2\cdot \sin 2\theta}{\text{g}}\)
Lama benda di udara
\(\text{t}_{\text{xmax}} = 2\times \dfrac{\text{v}_{0}\cdot \sin \theta}{\text{g}}\)
Rumus singkat ini hanya berlaku untuk gerak satu parabola yang simetris, seperti gerak benda dari permukaan tanah dan jatuh kembali ke tanah.
