Soal 1
Sebuah peluru meriam ditembakkan dengan kelajuan awal 60 m/s pada sudut elevasi \(37^{\circ}\). Jika \(\text{g} = 10 \text{ ms}^{-2}\), maka posisi peluru pada detik ke-3 adalah …
(A) \(x = 140\text{ m}, y = 60\text{ m}\)
(B) \(x = 140\text{ m}, y = 63\text{ m}\)
(C) \(x = 144\text{ m}, y = 60\text{ m}\)
(D) \(x = 144\text{ m}, y = 63\text{ m}\)
(E) \(x = 145\text{ m}, y = 63\text{ m}\)
Jawaban: D
Langkah 1: menentukan ketinggian
\(\text{y} = \text{y}_{0} + \text{v}_{0\text{y}}\cdot \text{t} \:-\:\frac{1}{2}\cdot \text{g}\cdot \text{t}^2\)
\(\text{y} = 0 + 60\cdot \sin 37^{\circ}\cdot 3 \:-\:\frac{1}{2}\cdot 10\cdot 3^2\)
\(\text{y} = 0 + 60\cdot 0,6\cdot 3 \:-\:\frac{1}{2}\cdot 10\cdot 9\)
\(\text{y} = 63\text{ m}\)
Langkah 2: menentukan jarak mendatar
\(\text{x} = \text{v}_{\text{x}}\cdot \text{t}\)
\(\text{x} = 60\cdot \cos 37^{\circ}\cdot 3\)
\(\text{x} = 60\cdot 0,8\cdot 3\)
\(\text{x} = 144 \text{ m}\)
Jadi posisi peluru pada detik ke-3 adalah \(x = 144\text{ m}, y = 63\text{ m}\)
Soal 2
Sebuah peluru ditembakkan dengan kelajuan awal 40 m/s pada sudut elevasi \(30^{\circ}\). Jika percepatan gravitasi di tempat tersebut \(10 \text{ ms}^{-2}\), maka ketinggian maksimum yang dapat dicapai peluru tersebut adalah …
(A) 10 m
(B) 15 m
(C) 20 m
(D) 25 m
(E) 50 m
Jawaban: C
Langkah 1: menentukan waktu sampai ketinggian maksimum
Pada saat mencapai titik tertinggi, \(\text{v}_{\text{y}} =0\)
\(\text{v}_{\text{y}} = \text{v}_{0\text{y}}\:-\:\text{g}\cdot \text{t}\)
\(0 = \text{v}_{0}\cdot \sin {30}^{\circ}\:-\:\text{g}\cdot \text{t}\)
\(0 = 40\cdot 0,5\:-\:10\cdot \text{t}\)
\(0 = 20\:-\:10\cdot \text{t}\)
\(\text{t} = 2\text{ detik}\)
Langkah 2: Menentukan tinggi maksimum
\(\text{y} = \text{y}_{0} + \text{v}_{0\text{y}}\cdot \text{t} \:-\:\frac{1}{2}\cdot \text{g}\cdot \text{t}^2\)
\(\text{y} = 0 + 40\cdot \sin {30}^{\circ}\cdot 2 \:-\:\frac{1}{2}\cdot 10\cdot 2^2\)
\(\text{y} = 40\cdot 0,5\cdot 2 \:-\:\frac{1}{2}\cdot 10\cdot 4\)
\(\text{y} = 40 \:-\:20\)
\(\text{y} = 20\text{ m}\)
Jadi, ketinggian maksimum yang dicapai peluru adalah 20 meter
Soal 3
Dari atas gedung setinggi 32 meter, sebuah bola dilempar dengan kelajuan awal 20 m/s pada sudut elevasi 37°. Jika percepatan gravitasi di tempat tersebut \(10 \text{ ms}^{-2}\), maka bola akan sampai ke permukaan tanah dalam waktu …
(A) 2 detik
(B) 3 detik
(C) 4 detik
(D) 5 detik
(E) 6 detik
Jawaban: C
Karena bola dilempar dari ketinggian 32 meter, maka \(\text{y}_0 = 80\text{ m}\)
\(\text{y} = \text{y}_{0} + \text{v}_{0\text{y}}\cdot \text{t} \:-\:\frac{1}{2}\cdot \text{g}\cdot \text{t}^2\)
Untuk menghitung waktu sampai ke permukaan tanah, masukkan nilai \(\text{y} = 0\)
\(0 = 32 + 20\cdot \sin {37}^{\circ}\cdot \text{t} \:-\:\frac{1}{2}\cdot 10\cdot \text{t}^2\)
\(0 = 32 + 20\cdot 0,6\cdot \text{t} \:-\:5\cdot \text{t}^2\)
\(0 = 32 + 12\text{t} \:-\:5\text{t}^2\)
\(5\text{t}^2\:-\:12\text{t}\:-\:32 = 0\)
\((5\text{t} + 8)(\text{t}\:-\:4) = 0\)
\(\text{t}\:-\:4 = 0\rightarrow \text{t} = 4\text{ s}\)
Jadi bola sampai ke permukaan tanah dalam waktu 4 detik
Soal 4
Sebuah peluru ditembakkan dari atas gedung setinggi 36 meter, dengan kelajuan awal 30 m/s dengan sudut elevasi 53°. Jika percepatan gravitasi di tempat tersebut \(10 \text{ ms}^{-2}\), maka kecepatan peluru sesaat sebelum menyentuh tanah adalah …
(A) \(\text{v} = 18\sqrt{2}\text{ m/s}, \theta = \tan^{-1} {(2)}\)
(B) \(\text{v} = 18\sqrt{3}\text{ m/s}, \theta = \tan^{-1} {(2)}\)
(C) \(\text{v} = 18\sqrt{3}\text{ m/s}, \theta = \tan^{-1} {(-2)}\)
(D) \(\text{v} = 18\sqrt{5}\text{ m/s}, \theta = \tan^{-1} {(-1)}\)
(E) \(\text{v} = 18\sqrt{5}\text{ m/s}, \theta = \tan^{-1} {(-2)}\)
Jawaban: E
Langkah 1: Menentukan lama peluru di udara
\(\text{y} = \text{y}_{0} + \text{v}_{0\text{y}}\cdot \text{t} \:-\:\frac{1}{2}\cdot \text{g}\cdot \text{t}^2\)
\(0 = 36 + 30\cdot \sin {53}^{\circ}\cdot \text{t} \:-\:\frac{1}{2}\cdot 10\cdot \text{t}^2\)
\(0 = 36 + 30\cdot 0,8\cdot \text{t} \:-\:5\text{t}^2\)
\(0 = 36 + 24\text{t} \:-\:5\text{t}^2\)
\(5\text{t}^2\:-\:24\text{t}\:-\:36 = 0\)
\((5\text{t} + 6)(\text{t}\:-\:6) = 0\)
\(\text{t}\:-\:6 = 0\rightarrow \text{t} = 6\text{ s}\)
Langkah 2: Menentukan komponen vektor kecepatan
Kecepatan arah sumbu-x
\(\text{v}_{\text{x}} = \text{v}_{0}\cdot \cos {53}^{\circ}\)
\(\text{v}_{\text{x}} = 30\cdot 0,6\)
\(\text{v}_{\text{x}} = 18 \text{ m/s}\)
Kecepatan arah sumbu-y
\(\text{v}_{\text{y}} = \text{v}_{0\text{y}}\:-\:\text{g}\cdot \text{t}\)
\(\text{v}_{\text{y}} = \text{v}_{0}\cdot \sin {53}^{\circ}\:-\:\text{g}\cdot \text{t}\)
\(\text{v}_{\text{y}} = 30\cdot 0,8\:-\:10\cdot 6\)
\(\text{v}_{\text{y}} = -36\text{ m/s}\)
Langkah 2: Menghitung resultan vektor kecepatan dan arahnya
\(\text{v} = \sqrt{(\text{v}_{\text{x}})^2 + (\text{v}_{\text{y}})^2}\)
\(\text{v} = \sqrt{18^2 + (-36)^2}\)
\(\text{v} = \sqrt{324 + 1296}\)
\(\text{v} = \sqrt{1620}\)
\(\text{v} = 18\sqrt{5}\text{ m/s}\)
\(\tan \theta = \dfrac{\text{v}_{y}}{\text{v}_{x}}\)
\(\tan \theta = \dfrac{-36}{18}\)
\(\tan \theta = -2\)
\(\theta = \tan^{-1} {(-2)}\)
Soal 5
Sebuah bola ditendang dengan kelajuan awal \(\text{v}_0\) pada sudut elevasi \(53^{\circ}\). Pada saat bola mencapai titik tertinggi, jarak mendatar yang ditempuh 76,8 meter. Jika percepatan gravitasi di tempat tersebut \(10 \text{ ms}^{-2}\), maka kelajuan awal bola tersebut adalah …
(A) 20 m/s
(B) 30 m/s
(C) 40 m/s
(D) 50 m/s
(E) 60 m/s
Jawaban: C
Langkah 1: Menentukan waktu sampai ketinggian maksimum
Pada saat mencapai titik tertinggi, \(\text{v}_{\text{y}} =0\)
\(\text{v}_{\text{y}} = \text{v}_{0\text{y}}\:-\:\text{g}\cdot \text{t}\)
\(0 = \text{v}_{0}\cdot \sin 53^{\circ}\:-\:10\text{t}\)
\(0 = \text{v}_{0}\cdot 0,8\:-\:10\text{t}\)
\(10\text{t} = 0,8\text{v}_{0}\)
\(\text{t} = 0,08\text{v}_{0}\text{ detik}\)
langkah 2: Menentukan kelajuan awal
\(\text{x} = \text{v}_{0\text{x}}\cdot t\)
\(76,8 = \text{v}_{0}\cdot \cos 53^{\circ}\cdot t\)
\(76,8 = \text{v}_{0}\cdot 0,6\cdot 0,08\cdot\text{v}_{0}\)
\(76,8 = 0,048\cdot (\text{v}_{0})^2\)
\((\text{v}_{0})^2 = \dfrac{76,8}{0,048} = \dfrac{76800}{48}\)
\((\text{v}_{0})^2 = 1600\)
\(\text{v}_{0} = \sqrt{1600}\)
\(\text{v}_{0} = 40 \text{ m/s}\)
Jadi kelajuan awal bola tersebut adalah 40 m/s
Soal 6
Sebuah bom dijatuhkan tanpa kecepatan awal dari pesawat terbang yang sedang melaju horizontal dengan kecepatan 720 km/jam, pada ketinggian 490 meter. Jarak mendatar terjauh bom tersebut sampai ke permukaan tanah jika diukur dari koordinat awal \(x\) bom dijatuhkan adalah … (gunakan \(\text{g} = 9,8 \text{ ms}^{-2}\))
(A) 1 km
(B) 2 km
(C) 3 km
(D) 4 km
(E) 5 km
Jawaban: B
Langkah 1: menentukan lama bom di udara
\(\text{y} = \text{y}_{0} + \text{v}_{0\text{y}}\cdot \text{t} \:-\:\frac{1}{2}\cdot \text{g}\cdot \text{t}^2\)
Bom tidak memiliki kecepatan awal dalam arah sumbu-y, sehingga \(\text{v}_{0\text{y}} = 0\)
\(0 = 490 + 0 \:-\:\frac{1}{2}\cdot 9,8\cdot \text{t}^2\)
\(0 = 490 + 0 \:-\:4,9\cdot \text{t}^2\)
\(4,9\cdot \text{t}^2 = 490\)
\(\text{t}^2 = \dfrac{490}{4,9}\)
\(\text{t}^2 = 100\)
\(\text{t} = \sqrt{100} = 10\text{ s}\)
Langkah 2: menentukan jarak mendatar terjauh
Kecepatan awal bom dalam arah sumbu-x sama dengan kecepatan pesawat yaitu 720 km/jam.
\(720 \text{ km/jam} = \dfrac{720.000 \text{ m}}{3600 \text{ s}}\)
\(720 \text{ km/jam} = 200\text{ m/s}\)
\(\text{x} = \text{v}_{0\text{x}}\cdot t\)
\(\text{x} = 200\cdot 10\)
\(\text{x} = 2000 \text{ meter}\)
Jadi, jarak mendatar bom tersebut sampai ke tanah adalah 2000 meter = 2 km
Soal 7
Sebuah peluru ditembakkan dengan kelajuan awal 50 m/s pada sudut elevasi 53º agar tepat masuk pada sebuah pipa berlubang yang terpasang miring dengan sudut 45° terhadap horizontal. Tentukan posisi lubang pipa saat peluru tepat memasukinya.
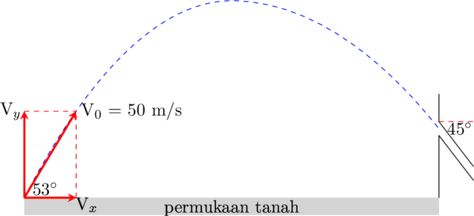
(A) (210, 30) meter
(B) (210, 35) meter
(C) (220, 50) meter
(D) (220, 60) meter
(E) (220, 60) meter
Jawaban: B
Langkah 1: Menentukan waktu saat peluru tepat masuk ke dalam pipa
\(\tan (-45^{\circ}) = \dfrac{\text{v}_{\text{y}}}{\text{v}_{\text{x}}}\)
\(-1 = \dfrac{\text{v}_{\text{y}}}{\text{v}_{\text{x}}}\)
\(\text{v}_{\text{y}} = – \text{v}_{\text{x}}\)
\(\text{v}_{0\text{y}}\:-\:\text{g}\cdot \text{t} = – \text{v}_{0\text{x}}\)
\(\text{v}_{0}\cdot \sin 53^{\circ}\:-\:\text{g}\cdot \text{t} = – \text{v}_{0}\cdot \cos 53^{\circ}\)
\(50\cdot 0,8\:-\:10\cdot \text{t} = -50\cdot 0,6\)
\(40\:-\:10\text{t} = – 30\)
\(40 + 30 = 10\text{t}\)
\(70 = 10\text{t}\)
\(\text{t} = 7 \text{ s}\)
Langkah 2: Menentukan ketinggian dan jarak mendatar pipa
Ketinggian pipa
\(\text{y} = \text{y}_{0} + \text{v}_{0}\cdot \sin 53^{\circ}\cdot \text{t} \:-\:\frac{1}{2}\cdot \text{g}\cdot \text{t}^2\)
\(\text{y} = 0 + 50\cdot 0,8\cdot 7 \:-\:\frac{1}{2}\cdot 10\cdot 7^2\)
\(\text{y} = 280 \:-\:245\)
\(\text{y} = 35\text{ meter}\)
Jarak mendatar pipa
\(\text{x} = \text{v}_{\text{x}}\cdot \text{t}\)
\(\text{x} = \text{v}_{0}\cdot \cos 53^{\circ} \cdot \text{t}\)
\(\text{x} = 50\cdot 0,6 \cdot 7\)
\(\text{x} = 210 \text{ m}\)
Jadi koordinat pipa tersebut saat peluru tepat masuk adalah (210, 35) meter
