Rangkaian Seri
Di bawah ini adalah gambar dua buah resistor yang dirangkai seri dengan sebuah sumber tegangan.
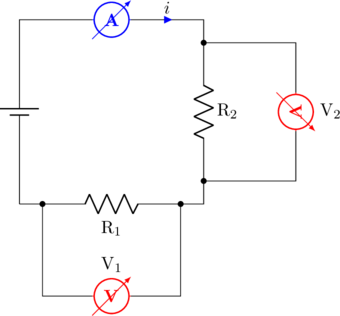
Besar hambatan pengganti untuk kedua resistor yang dipasang seri adalah:
\(\text{R}_{\text{pengganti}} = \text{R}_1 + \text{R}_2\)
Besarnya kuat arus listrik yang melalui kedua resistor yang dirangkai seri adalah sama
\(i_{\text{total}} = i_1 = i_2\)
Beda potensial pada titik-titik ujung resistor pertama adalah \(V_1\) sedangkan pada resistor yang kedua adalah \(V_2\)
\(V_{\text{sumber}} = V_1 + V_2\)
Rangkaian Paralel
Di bawah ini adalah gambar tiga buah resistor yang dirangkai paralel dengan sebuah sumber tegangan.
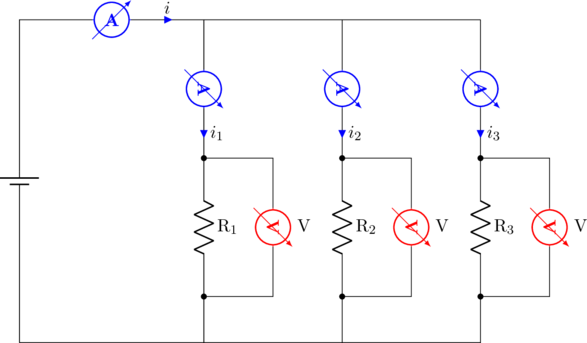
Besar hambatan pengganti untuk tiga buah resistor yang dipasang paralel adalah:
\(\dfrac{1}{\text{R}_{\text{pengganti}}} = \dfrac{1}{\text{R}_1} + \dfrac{1}{\text{R}_2} + \dfrac{1}{\text{R}_3}\)
Kuat arus listrik yang melalui \(\text{R}_1\) adalah \(i_1\)
Kuat arus listrik yang melalui \(\text{R}_2\) adalah \(i_2\)
Kuat arus listrik yang melalui \(\text{R}_3\) adalah \(i_3\)
\(i_{\text{total}} = i_1 + i_2 + i_3\)
Beda potensial pada ketiga resistor yang dirangkai paralel adalah sama
LATIHAN SOAL
Soal 01
Perhatikan rangkaian listrik di bawah ini:
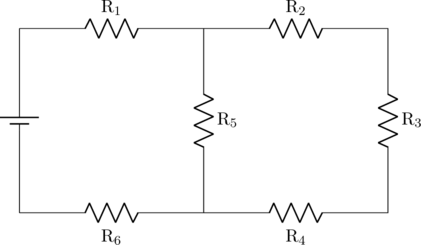
\(\text{R}_1 = 2 \:\Omega\), \(\text{R}_2 = 3 \:\Omega\), \(\text{R}_3 = 2\: \Omega\), \(\text{R}_4 = 5 \:\Omega\), \(\text{R}_5 = 10\: \Omega\), \(\text{R}_6 = 3\: \Omega\), dan tegangan baterai \(\text{V} = 12 \text{ volt}\)
Tentukan:
(A) Besar hambatan pengganti total
(B) Kuat arus total
(C) Kuat arus yang melalui \(\text{R}_5\)
(D) Beda potensial pada kedua ujung \(\text{R}_5\)
(A) Menghitung besar hambatan pengganti total
Berikut ini adalah tahapan dalam menentukan besar hambatan pengganti total
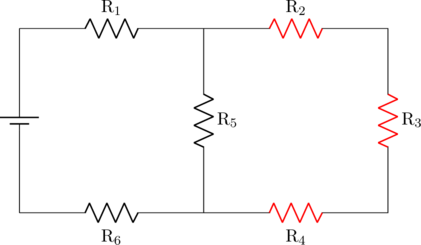
\(\text{R}_2\), \(\text{R}_3\), dan \(\text{R}_4\) terangkai seri
\(\text{R}_{2,3,4} = \text{R}_2 + \text{R}_3 + \text{R}_4\)
\(\text{R}_{2,3,4} = 3 + 2 + 5\)
\(\text{R}_{2,3,4} = 10 \Omega\)
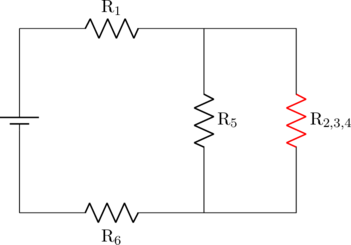
Selanjutnya, \(\text{R}_{2,3,4}\) dan \(\text{R}_5\) terangkai paralel.
\(\dfrac{1}{\text{R}_{2,3,4,5}} = \dfrac{1}{\text{R}_{2,3,4}} + \dfrac{1}{\text{R}_5}\)
\(\dfrac{1}{\text{R}_{2,3,4,5}} = \dfrac{1}{10} + \dfrac{1}{10}\)
\(\dfrac{1}{\text{R}_{2,3,4,5}} = \dfrac{1}{5}\)
\(\text{R}_{2,3,4,5} = 5 \Omega\)

\(\text{R}_1\), \(\text{R}_{2,3,4,5}\), dan \(\text{R}_6\) terangkai seri
\(\text{R}_{\text{total}} = \text{R}_1 + \text{R}_{2,3,4,5} + \text{R}_6\)
\(\text{R}_{\text{total}} = 2 + 5 + 3\)
\(\text{R}_{\text{total}} = 10 \Omega\)
Jadi besar hambatan pengganti totalnya adalah 10 ohm
(B) Menghitung kuat arus total
\(i_{\text{total}} = \dfrac{\text{V}}{\text{R}_{\text{total}}}\)
\(i_{\text{total}} = \dfrac{12}{10}\)
\(i_{\text{total}} = 1,2 \text{ ampere}\)
(C) Menghitung kuat arus yang melalui \(\text{R}_5\)
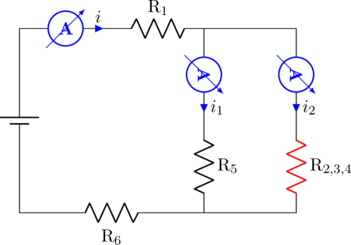
Arus listrik yang melalui \(\text{R}_5\) adalah \(i_1\)
Pada rangkaian paralel kuat arus listrik berbanding terbalik dengan resistor yang dilaluinya.
\(i_1 : i_2 = \dfrac{1}{\text{R}_5} : \dfrac{1}{\text{R}_{2,3,4}}\)
\(i_1 : i_2 = \dfrac{1}{10} :\dfrac{1}{10}\)
\(i_1 : i_2 = 1 : 1\)
\(i_1 = \dfrac{1}{1 + 1} \times i_{\text{total}}\)
\(i_1 = \dfrac{1}{2} \times 1,2 = 0,6 \text{ ampere}\)
(D) Beda potensial pada kedua ujung \(\text{R}_5\)
\(\text{V}_5 = i_1 \times \text{R}_5\)
\(\text{V}_5 = 0,6 \times 10\)
\(\text{V}_5 = 6 \text{ volt}\)
Soal 02
Perhatikan rangkaian listrik di bawah ini:
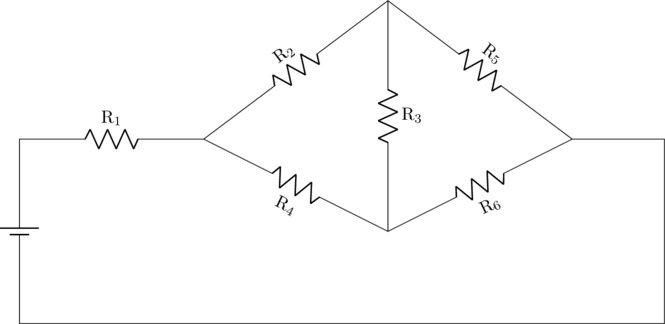
\(\text{R}_1 = 4\: \Omega\), \(\text{R}_2 = 5\: \Omega\), \(\text{R}_3 = 21\: \Omega\), \(\text{R}_4 = 10\: \Omega\), \(\text{R}_5 = 1 \:\Omega\), \(\text{R}_6 = 2 \:\Omega\), dan tegangan baterai \(\text{V} = 16 \text{ volt}\)
Tentukan:
(A) Besar hambatan pengganti total
(B) Kuat arus total
(C) Kuat arus yang melalui \(\text{R}_2\)
(D) Beda potensial pada kedua ujung \(\text{R}_2\)
(A) Menentukan besar hambatan pengganti total
Terdapat jembatan wheatstone pada rangkaian resistor, sehingga \(\text{R}_3\) dapat dihilangkan karena tidak ada arus listrik yang melewatinya.
\(\text{R}_2 \times \text{R}_6 = \text{R}_4 \times \text{R}_5\)
\(5 \times 2 = 10 \times 1\)
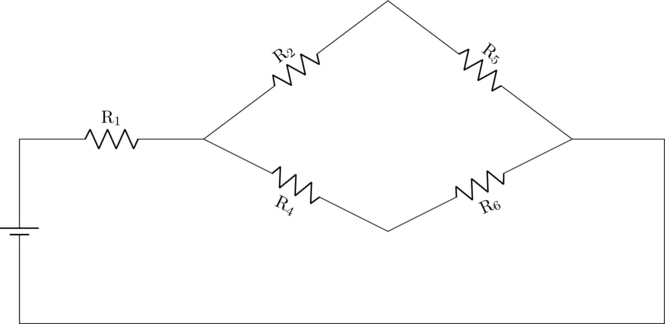
\(\text{R}_2\) dan \(\text{R}_5\) terangkai seri sehingga:
\(\text{R}_{2,5} = \text{R}_2 + \text{R}_5\)
\(\text{R}_{2,5} = 5 + 1\)
\(\text{R}_{2,5} = 6 \:\Omega\)
\(\text{R}_4\) dan \(\text{R}_6\) terangkai seri sehingga:
\(\text{R}_{4,6} = \text{R}_4 + \text{R}_6\)
\(\text{R}_{4,6} = 10 + 2\)
\(\text{R}_{4,6} = 12 \:\Omega\)
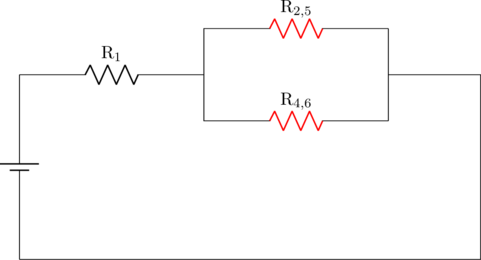
\(\text{R}_{2,5}\) dan \(\text{R}_{4,6}\) terangkai paralel
\(\dfrac{1}{\text{R}_{2,4,5,6}} = \dfrac{1}{\text{R}_{2,5}} + \dfrac{1}{\text{R}_{4,6}}\)
\(\dfrac{1}{\text{R}_{2,4,5,6}} = \dfrac{1}{6} + \dfrac{1}{12}\)
\(\dfrac{1}{\text{R}_{2,4,5,6}} = \dfrac{3}{12}\)
\(\text{R}_{2,4,5,6} = 4 \:\Omega\)
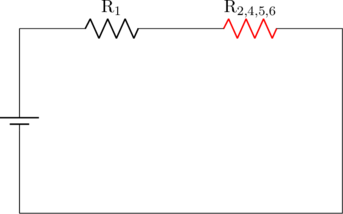
\(\text{R}_1\) dan \(\text{R}_{2,4,5,6}\) terangkai seri
\(\text{R}_{\text{total}} = \text{R}_1 + \text{R}_{2,4,5,6}\)
\(\text{R}_{\text{total}} = 4 + 4\)
\(\text{R}_{\text{total}} = 8 \:\Omega\)
(B) Menentukan kuat arus total
\(i_{\text{total}} = \dfrac{\text{V}}{\text{R}_{\text{total}}}\)
\(i_{\text{total}} = \dfrac{16}{8}\)
\(i_{\text{total}} = 2 \text{ ampere}\)
(C) Menghitung kuat arus yang melalui \(\text{R}_2\)
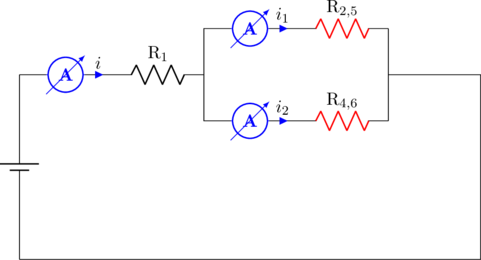
Arus listrik yang melalui \(\text{R}_2\) adalah \(i_1\)
Pada rangkaian paralel kuat arus listrik berbanding terbalik dengan resistor yang dilaluinya.
\(i_1 : i_2 = \dfrac{1}{\text{R}_{2,5}} : \dfrac{1}{\text{R}_{4,6}}\)
\(i_1 : i_2 = \dfrac{1}{6} :\dfrac{1}{12}\)
\(i_1 : i_2 = 2 : 1\)
\(i_1 = \dfrac{2}{2 + 1} \times i_{\text{total}}\)
\(i_1 = \dfrac{2}{3} \times 2 = \dfrac{4}{3} \text{ ampere}\)
(D) Beda potensial pada kedua ujung \(\text{R}_2\)
\(\text{V}_2 = i_1 \times \text{R}_2\)
\(\text{V}_2 = \dfrac{4}{3} \times 5\)
\(\text{V}_2 = \dfrac{20}{3} \text{ volt}\)
