Dua partikel bermuatan negatif \((q_1)\) dan positif \((q_2)\), terpisah sejauh \(r\), akan mengalami gaya tarik-menarik.

Dua partikel bermuatan sejenis \(q_1\) dan \(q_2\) terpisah sejauh \(r\) akan mengalami gaya tolak-menolak.

Besar gaya Coulomb antara dua partikel bermuatan listrik
$$\bbox[ 5px, border: 2px solid red] {\text{F} = \dfrac{1}{ 4\pi \varepsilon_0} \cdot \dfrac{q_1 \cdot q_2}{r^2}}$$
atau
$$\bbox[ 5px, border: 2px solid red] {\text{F} = k \cdot \dfrac{q_1 \cdot q_2}{r^2}}$$
Besar gaya Coulomb sebanding dengan perkalian kedua muatan partikel dan berbanding terbalik dengan kuadrat jarak antara kedua partikel.
Note:
\(k\) disebut konstanta Coulomb
Nilai \(k\) saat kedua partikel berada di udara atau di ruang hampa udara (vakum) berkisar \(9 \times 10^9 \:\: \text{N} \cdot \text{m}^2 \cdot \text{C}^{-2}\)
\(r\) adalah jarak antara kedua partikel
Dalam perhitungan besar gaya Coulomb tanda untuk muatan (+) atau (-) tidak ditulis
Besar gaya Coulomb antara dua partikel bermuatan listrik pada medium tertentu
$$\bbox[ 5px, border: 2px solid red] {\text{F}_{\text{medium}} = \dfrac{1}{\varepsilon_r}\cdot k \cdot \dfrac{q_1 \cdot q_2}{r^2}}$$
$$\bbox[ 5px, border: 2px solid red] {\text{F}_{\text{medium}} = \dfrac{1}{\varepsilon_r}\cdot \text{F}}$$
Note:
\(\varepsilon_r\) adalah permitivitas relatif atau konstanta dielektrik
\(\varepsilon_0\:\text{ (permitivitas ruang hampa) } = 8,85 \times 10^{-12}\:\: \text{C}^2\cdot \text{N}^{-1} \cdot \text{m}^{-2}\)
Konversi satuan
\(1 \mu \text{C} = 1 \times 10^{-6} \text{ C}\)
\(1 \text{ cm} = 1 \times 10^{-2} \text{ m}\)
SOAL LATIHAN
Soal 01
Dua bola bermuatan kecil terpisah sejauh 0,05 m dan saling tolak-menolak dengan gaya \(18 \times 10^{-4} \text{ N}\). Ketika bola bermuatan terpisah sejauh 0,15 m dalam medium yang sama, gaya tolak-menolak sebesar…
(A) \(1 \times 10^{-4} \text{ N}\)
(B) \(2 \times 10^{-4} \text{ N}\)
(C) \(3 \times 10^{-4} \text{ N}\)
(D) \(6 \times 10^{-4} \text{ N}\)
(E) \(8 \times 10^{-4} \text{ N}\)
Jawaban: B
Gaya tolak-menolak antara dua bola bermuatan berbanding terbalik dengan kuadrat jarak kedua bola.
\(\dfrac{\text{F}_1}{\text{F}_2} = \left(\dfrac{r_2}{r_1}\right)^2\)
\(\dfrac{18 \times 10^{-4}}{\text{F}_2} = \left(\dfrac{0,15}{0,05}\right)^2\)
\(\dfrac{18 \times 10^{-4}}{\text{F}_2} = 3^2\)
\(\dfrac{18 \times 10^{-4}}{\text{F}_2} = 9\)
\(\text{F}_2 = \dfrac{18 \times 10^{-4}}{9}\)
\(\text{F}_2 = 2 \times 10^{-4} \text{ N}\)
Soal 02
Dua buah muatan terpisah pada jarak \(r\) di udara, mengalami gaya tarik-menarik sebesar \(\text{F}\). Jika besar salah satu muatan digandakan, jaraknya dijadikan \(\dfrac{1}{2}\) kali semula, dan dicelupkan kedalam suatu zat yang memiliki konstanta dielektrik 2, maka besar gaya tarik-menarik antara kedua muatan tersebut sebesar…
(A) \(2\text{F}\)
(B) \(3\text{F}\)
(C) \(4\text{F}\)
(D) \(5\text{F}\)
(E) \(6\text{F}\)
Jawaban: C
F adalah besar gaya tarik-menarik antara dua buah benda bermuatan saat berada di udara.
\(\text{F} = k \cdot \dfrac{q \cdot q}{r^2}\)
\(\text{F} = k \cdot \dfrac{q^2}{r^2}\)
F’ adalah besar gaya tarik-menarik antara dua buah benda bermuatan saat berada di medium lain yang memiliki konstanta dielektrik \(\varepsilon_r = 2\)
\(\text{F’} = \dfrac{1}{\varepsilon_r } \cdot k \cdot \dfrac{2q \cdot q}{\left(\dfrac{1}{2}r\right)^2}\)
\(\text{F’} = \dfrac{1}{2} \cdot k \cdot \dfrac{2q^2}{\dfrac{1}{4}r^2}\)
\(\text{F’} = \dfrac{1}{\cancel{2}} \cdot k \cdot \dfrac{\cancel{2} \cdot q^2}{\dfrac{1}{4}r^2}\)
\(\text{F’} = 4 \cdot k \cdot \dfrac{ q^2}{r^2}\)
\(\text{F’} = 4 \cdot \text{F}\)
Soal 03
Dua buah muatan diletakkan pada suatu garis bilangan. \(Q_1 = + 20 \mu \text{C}\) pada \(X = -5 \text{ cm}\) dan \(Q_2 = -45 \mu \text{C}\) pada \(X = +10 \text{ cm}\). Muatan \(Q_3\) diletakkan pada koordinat X, sehingga ketiga muatan menjadi setimbang (resultan gaya di semua muatan nol).
Tentukan:
(A) Letak \(Q_3\)
(B) Jenis dan besar \(Q_3\)
Jawaban: (A) x = -35 cm (B) Q3 = -180 μC
Karena \(Q_1\) dan \(Q_2\) berbeda jenis muatan, maka \(Q_3\) diletakkan di luar daerah antara \(Q_1\) dan \(Q_2\) dekat yang muatannya paling kecil.
\(Q_3\) diletakkan di sebelah kiri \(Q_1\) agar resultan gaya di \(Q_3\) dapat nol
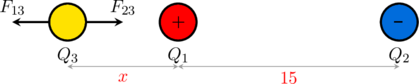
\(\text{F}_{13} = \text{F}_{23}\)
\(\cancel{k} \cdot \dfrac{Q_1 \cdot \cancel{Q_3}}{r^2_{13}} = \cancel{k} \cdot \dfrac{Q_2 \cdot \cancel{Q_3}}{r^2_{23}}\)
\(\dfrac{20}{x^2} = \dfrac{45}{(15 + x)^2}\)
\(\sqrt{\dfrac{20}{x^2}} = \sqrt{\dfrac{45}{(15 + x)^2}}\)
\(\dfrac{2}{x} = \dfrac{3}{15 + x}\)
\(30 + 2x = 3x\)
\(x = 30\)
Letak \(Q_3\) berada di sebelah kiri muatan \(Q_1\) sejauh 30 cm
atau dengan kata lain
Letak \(Q_3\) pada \(X = -35 \text{ cm}\) (letaknya diukur dari titik asal (0, 0))

Agar resultan gaya di \(Q_1\) juga nol, maka jenis muatan \(Q_3\) harus negatif
\(\text{F}_{31} = \text{F}_{21}\)
\(k \cdot \dfrac{Q_3 \cdot Q_1}{r^2_{31}} = k \cdot \dfrac{Q_2 \cdot Q_1}{r^2_{21}}\)
\(\dfrac{Q_3}{30^2} = \dfrac{45}{15^2}\)
\(Q_3 = \dfrac{45}{225} \times 900\)
\(Q_3 = 45\times 4\)
\(Q_3 = 180 \mu \text{C}\)
Jadi besar muatan ketiga adalah 180 μC
Soal 04
Total dua muatan \(q_1\) dan \(q_2\) adalah \(6 \mu \text{C}\). Jika kedua muatan tersebut dipisahkan sejauh 3 dm, setiap muatan akan merasakan gaya listrik sebesar 4 N. Besar \(q_1\) dan \(q_2\) berturut-turut adalah…
(A) \(-4 \mu \text{C}\) dan \(10 \mu \text{C}\)
(B) \(3 \mu \text{C}\) dan \(3 \mu \text{C}\)
(C) \(4 \mu \text{C}\) dan \(2 \mu \text{C}\)
(D) \(5 \mu \text{C}\) dan \(1 \mu \text{C}\)
(E) \(8 \mu \text{C}\) dan \(-2 \mu \text{C}\)
Jawaban: A
\(r = 3 \text{ dm} = 3 \times 10^{-1} \text{ m}\)
\(\color{blue}\text{F} = k\dfrac{q_1 \cdot q_2}{r^2}\)
\(4 \text{ N} = 9 \times 10^9\dfrac{q_1 \cdot q_2}{(3 \times 10^{-1})^2}\)
\(4 = \cancel{9} \times 10^9\dfrac{q_1 \cdot q_2}{\cancel{9} \times 10^{-2}}\)
\(4 = 1 \times 10^{11} \cdot q_1 \cdot q_2\)
\(4 \times 10^{-11} = q_1 \cdot q_2\)
\(40 \times 10^{-12} = q_1 \cdot q_2\)
\(40 (\:\mu \text{C})^2 = q_1 \cdot q_2\dotso \color{red} (1)\)
\(q_1 + q_2 = 6 \:\mu \text{C}\dotso \color{red} (2)\)
Dari pilihan jawaban yang tersedia, yang paling mungkin menjadi jawaban tepat adalah A karena kedua muatan kalau dikali menghasilkan angka 40 dan kalau dijumlahkan menghasilkan angka 6
Soal 05
Muatan \(+Q\) Coulomb ditempatkan di \(x = -1\) meter dan muatan \(-2Q\) Coulomb ditempatkan di \(x = +1\) meter. Muatan uji \(+q\) Coulomb yang diletakkan di sumbu X akan mengalami gaya total nol jika muatan tersebut diletakkan di \(x = \dotso\)
(A) \(-(3 + \sqrt{8})\) meter
(B) \(-\dfrac{1}{3}\) meter
(C) \(0\) meter
(D) \(\dfrac{1}{3}\) meter
(E) \((3 + \sqrt{8})\) meter
Jawaban: A
Agar muatan uji \(+q\) mengalami gaya total nol, maka muatan uji tersebut harus diletakkan di sebelah kiri muatan \(+Q\).

\(F_{13}\) = gaya tolak-menolak antara muatan \(+q\) dengan \(+Q\)
\(F_{23}\) = gaya tarik-menarik antara muatan \(+q\) dengan \(-2Q\)
Muatan uji \(+q\) mengalami gaya total nol, maka \(\color{blue} F_{13} = F_{23}\)
Note: tanda muatan tidak ikut dalam perhitungan gaya Coulomb
\(F_{13} = F_{23}\)
\(k \cdot \dfrac{Q \cdot q}{x^2} = k \cdot \dfrac{2Q \cdot q}{(2 + x)^2}\)
\(\cancel{k} \cdot \dfrac{\cancel{Q} \cdot \cancel{q}}{x^2} = \cancel{k} \cdot \dfrac{2\cancel{Q} \cdot \cancel{q}}{(2 + x)^2}\)
\(\dfrac{1}{x^2} = \dfrac{2}{(2 + x)^2}\)
\(\sqrt{\dfrac{1}{x^2}} = \sqrt{\dfrac{2}{(2 + x)^2}}\)
\(\dfrac{1}{x} = \dfrac{\sqrt{2}}{2 + x}\)
\(2 + x = \sqrt{2}x\)
\(2 = \sqrt{2}x \:-\:x\)
\(2 = (\sqrt{2} \:-\:1)x\)
\(x = \dfrac{2}{\sqrt{2}\:-\:1} \times \color{blue} \dfrac{\sqrt{2} + 1}{\sqrt{2} + 1}\)
\(x = 2 + 2\sqrt{2}\)
\(x = 2 + \sqrt{8}\)
Posisi muatan uji dalam sumbu X diukur dari koordinat titik asal (0,0) adalah di \(x = -1 – (2 + \sqrt{8}) = – (3 + \sqrt{8})\) meter.
Soal 06
Diagram berikut menunjukkan tiga bola kecil bermuatan listrik.
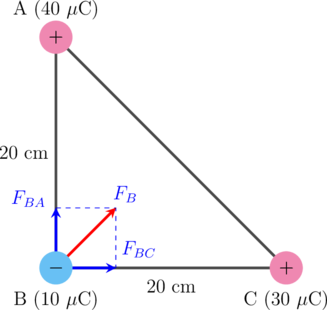
Besar gaya yang bekerja pada bola B adalah…
(A) 50 N
(B) 75 N
(C) 100 N
(D) 112,5 N
(E) 125 N
Jawaban: D
\(\text{F}_{\text{BC}} = k \cdot \dfrac{Q_B \times Q_C}{(r_{BC})^2}\)
\(\text{F}_{\text{BC}} = 9 \times 10^{9} \cdot \dfrac{10 \times 10^{-6} \times 30 \times 10^{-6}}{(20 \times 10^{-2})^2}\)
\(\text{F}_{\text{BC}} = 9 \times 10^{9} \cdot \dfrac{300 \times 10^{-12}}{400 \times 10^{-4}}\)
\(\text{F}_{\text{BC}} = \dfrac{27}{4} \times 10^{1}\)
\(\text{F}_{\text{BC}} = \dfrac{135}{2}\text{ N}\)
\(\text{F}_{\text{BA}} = k \cdot \dfrac{Q_B \times Q_A}{(r_{BA})^2}\)
\(\text{F}_{\text{BA}} = 9 \times 10^{9} \cdot \dfrac{10 \times 10^{-6} \times 40 \times 10^{-6}}{(20 \times 10^{-2})^2}\)
\(\text{F}_{\text{BA}} = 9 \times 10^{9} \cdot \dfrac{400 \times 10^{-12}}{400 \times 10^{-4}}\)
\(\text{F}_{\text{BA}} = 90 \text{ N}\)
\(\text{F}_{\text{B}} = \sqrt{ (\text{F}_{\text{BC}})^2 + (\text{F}_{\text{BA}})^2 }\)
\(\text{F}_{\text{B}} = \sqrt{ ( \dfrac{135}{2})^2 + 90^2 }\)
\(\text{F}_{\text{B}} = \sqrt{ \dfrac{18225}{4} + 8100 }\)
\(\text{F}_{\text{B}} = \sqrt{ \dfrac{50625}{4} }\)
\(\text{F}_{\text{B}} = \dfrac{225}{2}\)
\(\text{F}_{\text{B}} = 112,5 \text{ N}\)
Soal 07
Tiga muatan sejenis dan sama besar Q terletak pada satu bidang. Jika pusat-pusat tiap muatan dihubungkan, terbentuk segitiga sama sisi dengan panjang sisi \(2a\).
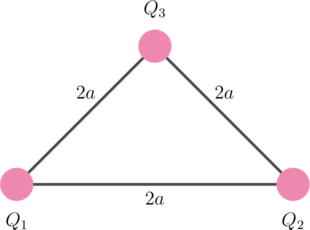
Besar gaya Coulomb yang dialami oleh salah satu muatan dinyatakan dalam \(k, Q, \text{ dan } a\) adalah…
(A) \(\dfrac{kQ^2}{a^2} \sqrt{3}\)
(B) \(\dfrac{kQ^2}{2a^2} \sqrt{3}\)
(C) \(\dfrac{kQ^2}{3a^2} \sqrt{3}\)
(D) \(\dfrac{kQ^2}{4a^2} \sqrt{3}\)
(E) \(\dfrac{kQ^2}{5a^2} \sqrt{3}\)
Jawaban: D
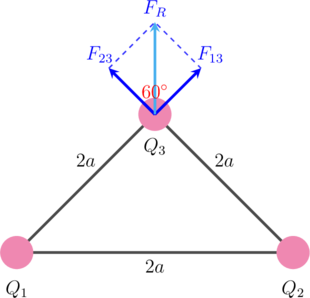
Segitiga sama sisi memiliki sudut yang besarnya masing-masing \(60^{\circ}\)
\(\text{F}_{\text{13}}= k\dfrac{Q_1 \cdot Q_3}{r^2}\)
\(\text{F}_{\text{13}}= k\dfrac{Q \cdot Q}{(2a)^2}\)
\(\text{F}_{\text{13}}= k\dfrac{Q^2}{4a^2}\)
\(\text{F}_{\text{23}} = \text{F}_{\text{13}} =\text{F} = k\dfrac{Q^2}{4a^2}\)
\(\text{F}_{R} = \sqrt{(\text{F}_{\text{23}} )^2 + (\text{F}_{\text{13}})^2 + 2 \cdot \text{F}_{\text{23}} \cdot \text{F}_{\text{13}} \cdot \cos 60^{\circ}}\)
\(\text{F}_{R} = \sqrt{(\text{F})^2 + (\text{F})^2 + 2 \cdot \text{F}\cdot \text{F} \cdot \dfrac{1}{2}}\)
\(\text{F}_{R} = \sqrt{3\cdot \text{F}^2}\)
\(\text{F}_{R} = \text{F}\cdot \sqrt{3}\)
\(\text{F}_{R} = k\dfrac{Q^2}{4a^2}\cdot \sqrt{3}\)
\(\text{F}_{R} = \dfrac{kQ^2}{4a^2} \sqrt{3}\)
