Dua buah kawat penghantar masing-masing berarus listrik disusun seperti gambar di bawah ini.
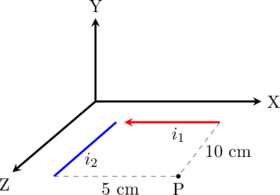
Jarak \(i_1\) dan \(i_2\) ke titik P masing-masing 10 cm dan 5 cm. Dua kawat penghantar dan titik P berada pada bidang XZ. Jika \(i_1 = 5 \text{ A}\), besar kuat arus yang mengalir pada kawat \(i_2\) agar kuat medan magnet di titik P sama dengan nol adalah…
(A) 0,5 A searah sumbu Z−
(B) 1,5 A searah sumbu Z+
(C) 1,5 A searah sumbu Z−
(D) 2,5 A searah sumbu Z−
(E) 2,5 A searah sumbu Z+
Jawaban: D
Dengan menggunakan aturan genggaman tangan kanan (jempol = arah arus, empat jari = arah medan magnet), arus pada kawat pertama \(i_1\) menimbulkan medan magnet di titik P ke arah atas \(\textbf{B}_1\).
Agar kuat medan magnet di P sama dengan nol, maka arah \(\textbf{B}_2\) di titik P ke bawah dengan besar yang sama dengan \(\textbf{B}_1\) sehingga arah arus \(i_2\) ke sumbu Z−.
\(\textbf{B}_1 = \textbf{B}_2\)
\(\dfrac{\cancel{\mu_0} \cdot i_1}{\cancel{2 \pi} a_1} = \dfrac{\cancel{\mu_0} \cdot i_2}{\cancel{2 \pi} a_2}\)
\(\dfrac{5}{10} = \dfrac{ i_2}{5}\)
\(i_2 = \dfrac{25}{10}\)
\(i_2 = 2,5 \text{ A}\) searah sumbu Z−
Soal 02
Sepotong kawat dengan panjang 50 cm dibentuk menjadi kawat yang melingkar berjari-jari 10 cm. Jika kawat dialiri arus listrik 2 A, besar medan magnet di pusat kawat melingkar adalah…
(A) \(5 \times 10^{-6} \text{ T}\)
(B) \(5\pi \times 10^{-6} \text{ T}\)
(C) \(1 \times 10^{-5} \text{ T}\)
(D) \(\pi \times 10^{-5} \text{ T}\)
(E) \(\pi \times 10^{-4} \text{ T}\)
Jawaban: C
\(\textbf{B} = \text{N} \cdot \dfrac{\mu_0 \cdot i}{2r}\)
\(\textbf{B} = \dfrac{l}{2\pi r} \cdot \dfrac{\mu_0 \cdot i}{2r}\)
\(\textbf{B} = \dfrac{0,5}{2\pi \cdot 0,1} \cdot \dfrac{4\pi \times 10^{-7} \cdot 2}{2(0,1)}\)
\(\textbf{B} = \dfrac{1 \times 10^{-7}}{1 \times 10^{-2}}\)
\(\textbf{B} = 1 \times 10^{-5} \text{ T}\)
Soal 03
Sebuah partikel bermuatan \(q = -0,04 \text{ C}\) bergerak masuk ke dalam daerah bermedan magnet seragam B dengan kecepatan \(v = 2 \times 10^{4} \text{ m/s}\) yang tegak lurus B. Akibatnya partikel tersebut mengalami gaya magnet \(\text{F}_{\text{B}} = 400 \text{ N}\).
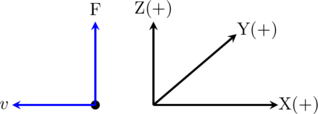
Dapat disimpulkan bahwa medan magnet B …
(A) 0,5 T ke arah sumbu Z negatif
(B) 0,5 T ke arah sumbu Z positif
(C) 0,5 T ke arah sumbu Y positif
(D) 0,5 T ke arah sumbu Y negatif
(E) 0,5 T ke arah sumbu X positif
Jawaban: C
\(\textbf{F} = \textbf{B} \cdot q \cdot v\)
\(400 = \textbf{B} \cdot 0,04 \cdot 2 \times 10^{4}\)
\(400 = \textbf{B} \cdot 8 \times 10^{2}\)
\(\textbf{B} = \dfrac{400}{8 \times 10^{2}}\)
\(\textbf{B} = 0,5 \text{ T}\) arah ke sumbu Y (+)
Note:
Gunakan aturan tangan kiri untuk partikel bermuatan negatif yang melewati medan magnet.
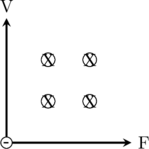
Ibu jari menunjukkan arah kecepatan partikel
Keempat jari menunjukkan arah medan magnet
Arah gaya (F) tegak lurus dengan telapak tangan dan ke arah luar.
Soal 04
Tiga buah konduktor yang cukup panjang A, B, dan C disusun sejajar pada jarak 10 cm satu sama lain dalam bidang dengan posisi B di tengah. Masing-masing konduktor dialiri arus listrik sebesar 3A, 2A, dan 1A yang arahnya sama. Besar gaya interaksi per satuan panjang pada konduktor C adalah…
(A) \(0,7 \:\mu \text{N/m}\)
(B) \(0,8 \:\mu \text{N/m}\)
(C) \(7 \:\mu \text{N/m}\)
(D) \(8 \:\mu \text{N/m}\)
(E) \(80 \:\mu \text{N/m}\)
Jawaban: C
Gunakan rumus: \(\color{blue} \dfrac{\text{F}}{l} = \dfrac{\mu_0 \cdot i_1 \cdot i_2}{2\pi \cdot a}\)
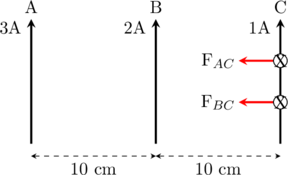
\(\dfrac{\text{F}}{l} = \dfrac{\text{F}_{\text{AC}}}{l} + \dfrac{\text{F}_{\text{BC}}}{l}\)
\(\dfrac{\text{F}}{l} = \dfrac{\mu_0 \cdot i_{\text{A}} \cdot i_{\text{C}}}{2\pi \cdot a_{\text{AC}}} + \dfrac{\mu_0 \cdot i_{\text{B}} \cdot i_{\text{C}}}{2\pi \cdot a_{\text{BC}}}\)
\(\dfrac{\text{F}}{l} = \dfrac{4\pi \times 10^{-7} \cdot 3 \cdot 1}{2\pi \cdot 20 \times 10^{-2}} + \dfrac{4\pi \times 10^{-7} \cdot 2 \cdot 1}{2\pi \cdot 10 \cdot 10^{-2}}\)
\(\dfrac{\text{F}}{l} = \dfrac{6 \times 10^{-7}}{2 \times 10^{-1}} + \dfrac{4 \times 10^{-7}}{1 \times 10^{-1}}\)
\(\dfrac{\text{F}}{l} = 3 \times 10^{-6} + 4 \times 10^{-6}\)
\(\dfrac{\text{F}}{l} = 7 \times 10^{-6} \text{ N/m}\)
\(\dfrac{\text{F}}{l} = 7\: \mu \text{ N/m}\)
Note:
Gunakan aturan tangan kanan untuk menentukan arah F

Ibu jari menunjukkan arah arus (I) (pada gambar ke arah atas)
Keempat jari menunjukkan arah medan magnet (B) (pada gambar bertanda silang artinya masuk bidang)
Arah F tegak lurus dengan telapak tangan ke arah luar (pada gambar ke arah kiri)
Soal 05
Sebuah partikel bermuatan +40 μC bergerak dengan kecepatan \(3 \times 10^5 \text{ m/s}\) sejajar searah dengan kawat penghantar yang dialiri arus 50 mA. Jika jarak partikel dari kawat penghantar sebesar 20 cm, besar dan arah gaya Lorenz yang dialami partikel tersebut adalah…
Jawaban:
\(\text{F} = \text{B} \cdot q \cdot v \sin \theta\)
\(\text{F} = \dfrac{\mu_0 \cdot i}{2 \pi \cdot a} \cdot q \cdot v \sin \theta\)
\(\text{F} = \dfrac{4\pi \times 10^{-7} \cdot 50 \times 10^{-3}}{2 \pi \cdot 20 \times 10^{-2}} \cdot 40 \times 10^{-6} \cdot 3 \times 10^{5} \sin 90^{\circ}\)
\(\text{F} = 6 \times 10^{-7} \text{ N}\) arah mendekati kawat penghantar.
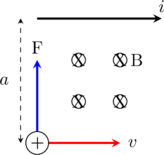
Note:
Gunakan aturan tangan kanan untuk partikel bermuatan positif yang melewati medan magnet.
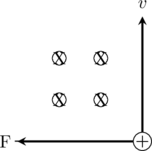
Ibu jari menunjukkan arah kecepatan partikel
Keempat jari menunjukkan arah medan magnet
Arah gaya (F) tegak lurus dengan telapak tangan dan ke arah luar.
