Persamaan gelombang stasioner ujung terikat
$$\bbox[yellow, 5px, border: 2px solid red] {y = 2A \sin kx \cos \omega t}$$
keterangan:
\(A = \text{ amplitudo gelombang berjalan}\)
\(k = \text{ bilangan gelombang}\)
\(\omega = \text{ kecepatan sudut gelombang}\)
\(x = \text{ posisi}\)
\(t = \text{ waktu}\)
Amplitudo Stasioner \(A_s = 2A \sin kx\)
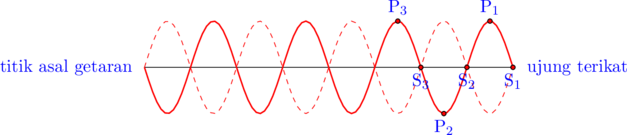
Letak simpul dari ujung terikat = \(\color{blue}\left(n\:-\:1 \right)\cdot \dfrac{\lambda}{2}\)
Letak perut dari ujung terikat = \(\color{blue} \left (n\:-\:\dfrac{1}{2}\right) \cdot\dfrac{\lambda}{2}\)
Persamaan gelombang stasioner ujung bebas
$$\bbox[yellow, 5px, border: 2px solid red] {y = 2A \cos kx \sin\omega t}$$
Amplitudo Stasioner \(A_s = 2A \cos kx\)
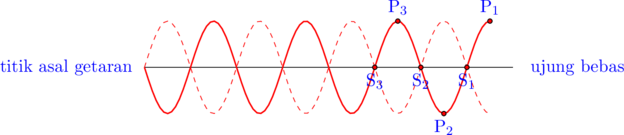
Letak simpul dari ujung terikat =\(\color{blue} \left(n\:-\:\dfrac{1}{2}\right)\cdot\dfrac{\lambda}{2}\)
Letak perut dari ujung terikat = \(\color{blue} \left(n\:-\:1\right) \cdot \dfrac{\lambda}{2}\)
LATIHAN SOAL
Soal 01
Sebuah tali salah satu ujungnya digetarkan terus-menerus dan ujung lainnya terikat kuat. Jika amplitudo yang diberikan adalah 10 cm, frekuensi 4 Hz dan cepat rambat gelombang pada tali 4 m/s, tentukanlah:
A. Amplitudo sebuah titik yang berjarak 1 m dari titik ikat
B. Jarak simpul ke-3 dari ujung terikat
C. Jarak perut ke-2 dari ujung terikat
Persamaan gelombang stasioner ujung terikat:
\(\color{blue} y = 2A \sin kx \cos \omega t\)
(A) Menghitung amplitudo gelombang stasioner
\(\color{blue} v = \lambda \cdot f\)
\(4 = \lambda \cdot 4\)
\(\lambda = 1 \text{ m}\)
\(\color{blue}k = \dfrac{2\pi}{\lambda}\)
\(k = \dfrac{2\pi}{1} = 2\pi\)
\(\color{blue} \text{A}_s = 2A \sin kx\)
\(\text{A}_s = 2(10 \text{ cm}) \sin 2\pi (1)\)
\(\text{A}_s = 2(10 \text{ cm}) \cdot 0\)
\(\text{A}_s = 0 \text{ cm}\)
B. Menghitung jarak simpul ke-3 dari ujung terikat
dengan rumus:
\(\color{blue} x = (n\:-\:1) \cdot \dfrac{\lambda}{2}\)
\(x = (3\:-\:1) \cdot \dfrac{1}{2}\)
\(x = (2) \cdot \dfrac{1}{2} = 1 \text{ m}\)
C. Menghitung jarak perut ke-2 dari ujung terikat
dengan rumus:
\(\color{blue} x = (n\:-\:\dfrac{1}{2}) \cdot \dfrac{\lambda}{2}\)
\(x = (2\:-\:\dfrac{1}{2}) \cdot \dfrac{1}{2}\)
\(x =\dfrac{3}{2}\cdot \dfrac{1}{2}\)
\(x =\dfrac{3}{4}\text{ m}\)
Soal 02
Seutas kawat yang panjangnya 100 cm direntangkan horizontal. Salah satu ujungnya digetarkan harmonik naik-turun dengan frekuensi 0,125 Hz dan amplitudo 16 cm dengan ujung lainnya terikat. Getaran harmonik tersebut merambat ke kanan dengan cepat rambat 4,5 cm/s. Tentukan letak simpul ke-4 dan perut ke-3 dari titik asal getaran.
Menghitung panjang gelombang:
\(v = \lambda \cdot f\)
\(4, 5 \times 10^{-2} = \lambda \cdot 0,125\)
\(\lambda = \dfrac{4, 5 \times 10^{-2} }{0,125}\)
\(\lambda = \dfrac{9 }{25} \text{ m}\)
Letak simpul ke-4 dari ujung terikat:
dengan rumus:
\(\color{blue} x = (n\:-\:1) \cdot \dfrac{\lambda}{2}\)
\( x = (4\:-\:1) \cdot \dfrac{\frac{9}{25}}{2}\)
\( x = (3) \cdot \dfrac{9}{50}\)
\( x = \dfrac{3}{50} \text{ m}\)
Letak simpul ke-4 dari titik asal getaran:
\(x = 1 \:-\:\dfrac{3}{50} = \color{red} \dfrac{47}{50} \text{ m}\)
Letak perut ke-3 dari ujung terikat:
\(\color{blue} x = (n\:-\:\dfrac{1}{2}) \cdot \dfrac{\lambda}{2}\)
\(x = (3\:-\:\dfrac{1}{2}) \cdot \dfrac{\frac{9}{25}}{2}\)
\(x = \dfrac{5}{2} \cdot \dfrac{9}{50}\)
\(x = \dfrac{9}{20}\)
Letak perut ke-3 dari titik asal getaran:
\(x = 1 \:-\:\dfrac{9}{20} = \color{red} \dfrac{11}{20} \text{ m}\)
Soal 03
Sebuah tali yang panjang, salah satu ujungnya digetarkan terus-menerus dengan amplitudo 10 cm, periode 2 s, sedangkan ujung yang lain dibuat bebas. Jika cepat rambat gelombang pada tali tersebut 18 cm/s dan pada tali terjadi gelombang stasioner, tentukan:
(A) amplitudo gelombang stasioner pada titik P yang berjarak 12 cm dari ujung bebas
(B) letak simpul ke-2 dan perut ke-3 dari ujung bebas.
Penyelesaian (A)
\(\color{blue} \text{A}_s = 2\text{A}\cos kx\)
\(v = \dfrac{\lambda}{\text{T}}\)
\(18 \times 10^{-2} \text{ m/s} = \dfrac{\lambda}{2}\)
\(\lambda = 36 \times 10^{-2} \text{ m}\)
\(\lambda = 0,36 \text{ m}\)
\(k = \dfrac{2\pi}{\lambda}\)
\(k = \dfrac{2\pi}{0,36}\)
\(k = \dfrac{50}{9} \pi\)
Amplitudo gelombang stasioner pada titik P yang berjarak 12 cm dari ujung bebas:
\(\text{A}_s = 2\text{A}\cos kx\)
\(\text{A}_s = 2\cdot 0,1 \text{ m} \cdot \cos \left( \dfrac{50}{9} \pi \cdot \dfrac{12}{100} \right)\)
\(\text{A}_s = 0,2 \cos \dfrac{2}{3} \pi\)
\(\text{A}_s = 0,2 \cdot (-0,5) = -0,1 \text{ m}\)
Penyelesaian (B)
Letak simpul ke-2 dari ujung bebas:
\(\color{blue} x = (n\:-\:\dfrac{1}{2}) \cdot \dfrac{\lambda}{2}\)
\(x = (2\:-\:\dfrac{1}{2}) \cdot \dfrac{\lambda}{2}\)
\(x =\dfrac{3}{2}\cdot \dfrac{0,36}{2}\)
\(x = 0,27 \text{ m}\)
Letak perut ke-3 dari ujung bebas:
dengan rumus:
\(\color{blue} x = (n\:-\:1) \cdot \dfrac{\lambda}{2}\)
\(x = (3\:-\:1) \cdot \dfrac{0,36}{2}\)
\(x = 0,36 \text{ m}\)
