Rumus Dasar
Frekuensi gelombang
$$\bbox[yellow, 5px, border: 2px solid red] {f = \dfrac{n}{t}}$$
\(n = \text{ banyak gelombang}\)
\(t = \text{ waktu tempuh gelombang}\)
Satuan frekuensi adalah Hz
Periode gelombang
$$\bbox[yellow, 5px, border: 2px solid red] {T= \dfrac{1}{f}}$$
Satuan periode adalah sekon
Gambar gelombang transversal:
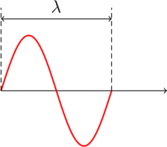
Cepat rambat gelombang
$$\bbox[yellow, 5px, border: 2px solid red] {v = \lambda \cdot f}$$
\(\lambda = \text{ panjang gelombang}\)
Cepat rambat gelombang transversal pada dawai
$$\bbox[yellow, 5px, border: 2px solid red] {v = \sqrt{\dfrac{\text{F}}{\mu}}}$$
\(\text{F} = \text{ gaya tegangan dawai (N)}\)
\(\mu = \text{ massa per satuan panjang dawai (kg/m)}\)
\(\mu = \dfrac{m}{l}\)
\(\mu = \dfrac{\rho \cdot V}{l} = \dfrac{\rho \cdot A \cdot \cancel{l}}{\cancel{l}} = \rho \cdot A \)
Hubungan Panjang Dawai (senar) dengan Panjang Gelombang yang Terbentuk
Frekuensi Nada Dasar \(\color{blue}f_0\)
\(\color{blue} f_0 = \dfrac{v}{2L}\)
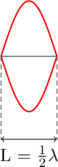
Frekuensi Nada Atas Pertama \(\color{blue}f_1\)
\(\color{blue} f_1 = \dfrac{v}{L}\)
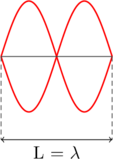
Frekuensi Nada Atas Kedua \(\color{blue} f_2\)
\(\color{blue} f_2 = \dfrac{v}{\frac{2}{3}L}\)
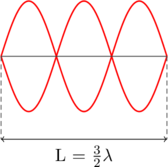
\(\color{blue} f_0 : f_1 : f_2 : \dotso = 1 : 2 : 3 : \dotso\)
Persamaan Simpangan, Kecepatan, dan Percepatan Gelombang Berjalan
Sebuah gelombang merambat ke arah kanan dari koordinat titik asal \((0, 0)\)
A. Persamaan Simpangan
$$\bbox[yellow, 5px, border: 2px solid red] {y = A\sin (\omega t \:-\:kx)}$$
Simpangan maksimum
Simpangan maksimum terjadi saat \(\sin (\omega t \:-\:kx) = 1\)
Simpangan maksimum = amplitudo gelombang
\(\color{blue} y_{\text{max}} = A\)
\(\omega (\text{ kecepatan sudut }) = 2\pi f\) dalam satuan rad/s
\(k (\text{ bilangan gelombang }) = \dfrac{2\pi}{\lambda}\)
B. Persamaan Kecepatan
$$\bbox[yellow, 5px, border: 2px solid red] {v = \omega A\cos (\omega t \:-\:kx)}$$
Kecepatan maksimum
Kecepatan maksimum terjadi saat \(\cos (\omega t \:-\:kx) = 1\)
\(\color{blue} v_{\text{max}} = \omega A\)
C. Persamaan Percepatan
$$\bbox[yellow, 5px, border: 2px solid red] {a = -\omega^2 A\sin (\omega t \:-\:kx)}$$
Percepatan maksimum
Percepatan maksimum terjadi saat \(\sin (\omega t \:-\:kx) = 1\)
\(\color{blue} a_{\text{max}} = -\omega^2 A\)
Sudut Fase dan Beda Fase
Dari persamaan gelombang berjalan \(\color{blue} y = A\sin (\omega t \:-\:kx)\)
Sudut fase = \(\omega t \:-\:kx = \dfrac{2\pi t}{T}\:-\:\dfrac{2\pi x}{\lambda}\)
Fase = \(\dfrac{\text{sudut fase}}{2\pi}\)
Fase = \(\dfrac{t}{T}\:-\:\dfrac{x}{\lambda}\)
Beda fase jika diketahui jarak antara titik A dan B
$$\bbox[yellow, 5px, border: 2px solid red] {\triangle \varphi = \dfrac{x_{\text{B}} \:-\: x_{\text{A}}}{\lambda}}$$
\(\color{blue} \triangle \varphi = \dfrac{\triangle x}{\lambda}\)
Beda fase jika diketahui perbedaan waktu titik A dan B
$$\bbox[yellow, 5px, border: 2px solid red] {\triangle \varphi = \dfrac{\triangle t}{T}}$$
LATIHAN SOAL
Soal 01
Dua balok kayu terapung pada permukaan air dan berjarak 200 cm satu sama lain. Keduanya turun-naik bersama permukaan air dengan frekuensi 8 getaran per sekon. Bila salah satu balok berada di puncak gelombang, balok yang lain berada di dasar gelombang, dan diantara kedua balok terdapat dua bukit gelombang, maka cepat rambat gelombang pada air tersebut adalah…
(A) 1,6 m/s
(B) 1,8 m/s
(C) 5,0 m/s
(D) 6,4 m/s
(E) 6,8 m/s
Jawaban: D
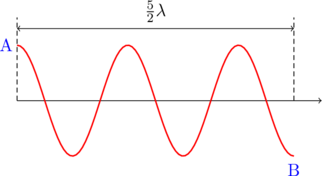
\(2\frac{1}{2} \lambda = 2 \text{ meter}\)
\(\lambda = \dfrac{2}{5} \times 2 \text{ meter}\)
\(\lambda = 0,8 \text{ meter}\)
\(f = \dfrac{n}{t} = \dfrac{8}{1} = 8 \text{ Hz}\)
\(v = \lambda \cdot f\)
\(v = 0,8\cdot 8\)
\(v = 6,4 \text{ m/s}\)
Soal 02
Dua gabus terapung di atas permukaan air terpisah 49 meter. Pada saat gelombang permukaan air datang dengan amplitudo 0,8 meter dan frekuensi 10 Hz, gabus P berada di puncak bukit gelombang, sedangkan gabus Q ada di lembah gelombang. Keduanya terpisah oleh tiga bukit gelombang. Jika gelombang datang dari gabus P dan waktu untuk gabus P adalah \(t\), tentukan persamaan getaran untuk:
(1) Gabus P
(2) Gabus Q
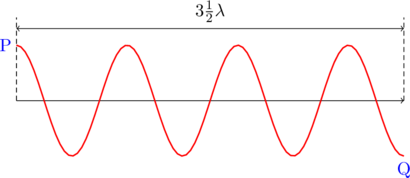
Amplitudo gelombang = 0,8 m
Frekuensi gelombang = 10 Hz
Panjang gelombang :
\(3\frac{1}{2} \lambda = 49 \text{ m}\)
\(\lambda = \dfrac{2}{7} \times 49 \text{ m}\)
\(\lambda = 14 \text{ m}\)
Kecepatan sudut gelombang:
\(\omega = 2\pi f\)
\(\omega = 2 \pi (10) = 20 \pi \text{ Hz}\)
Bilangan gelombang:
\(k = \dfrac{2\pi}{\lambda}\)
\(k = \dfrac{2\pi}{14}\)
\(k = \dfrac{\pi}{7}\)
Persamaan gelombang yang merambat ke arah kanan:
\(y = A \sin (\omega t\:-\:kx)\)
Persamaan getaran gabus P
\(y = A \sin (\omega t\:-\:kx)\)
Substitusi nilai A, ω, k, dan \(x = 0 \text{ m}\)
\(y_p = 0,8 \sin (20\pi t \:-\:\frac{\pi}{7}(0))\)
\(y_p = 0,8 \sin (20\pi t)\)
Persamaan getaran gabus Q
\(y = A \sin (\omega t\:-\:kx)\)
Substitusi nilai A, ω, k, dan \(x = 49 \text{ m}\)
\(y_p = 0,8 \sin (20\pi t \:-\:\frac{\pi}{7}(49))\)
\(y_p = 0,8 \sin (20\pi t\:-\:7\pi)\)
Soal 03
Kawat tembaga berdiameter 2,4 mm dan panjang 3 m mengalami tegangan karena pada ujung bawahnya digantungkan beban yang massanya 2 kg. Jika kawat dipukul dengan sebuah pensil, maka menjalarlah gelombang transversal di dalamnya. Jika massa jenis tembaga 8920 kg/m³, maka laju rambat gelombang tersebut adalah…
(A) \(5 \sqrt{5} \text{ m/s}\)
(B) \(8 \sqrt{5} \text{ m/s}\)
(C) \(9 \sqrt{5} \text{ m/s}\)
(D) \(10 \sqrt{5} \text{ m/s}\)
(E) \(12 \sqrt{5} \text{ m/s}\)
Jawaban: D
\(\color{blue} v = \sqrt{\dfrac{\text{F}}{\mu}}\)
\(\text{F} = m \cdot g\)
\(\text{F} = 2 \cdot 10 = 20 \text{ N}\)
\(\mu = \dfrac{m}{l} = \dfrac{\rho \cdot A \cdot l}{l} = \rho \cdot A\)
\(\mu = \rho \cdot \pi \cdot r^2\)
\(\mu = 8920 \cdot \dfrac{22}{7}\cdot (1,2 \times 10^{-3})^2 = 0,04 \text{ kg/m}\)
\(v = \sqrt{\dfrac{\text{F}}{\mu}}\)
\(v = \sqrt{\dfrac{20 }{0,04}}\)
\(v = 10 \sqrt{5} \text{ m/s}\)
Soal 04
Diketahui persamaan gelombang berjalan \(y = 0,05 \sin \pi(100t\:-\:0,02x)\) dengan y dan x dalam meter, dan t dalam sekon.
Manakah pernyataan di bawah ini yang benar?
(1) Amplitudo gelombang 0,05 cm
(2) Frekuensi gelombang 50 Hz
(3) panjang gelombang 0,02 m
(4) cepat rambat gelombang \(5 \times 10^3 \text{ m/s}\)
Jawaban: (2) dan (4)
(1) Amplitudo gelombang seharusnya 0,05 meter karena y dalam meter
(2) Menghitung frekuensi gelombang
\(\omega = 100 \pi\)
\(2\pi f = 100 \pi\)
\(f = \dfrac{100}{2} = 50 \text{ Hz}\)
(3) Panjang gelombang seharusnya 100 meter
\(k = 0,02 \pi\)
\(\dfrac{2\pi}{\lambda} = 0,02 \pi\)
\(\lambda = \dfrac{2}{0,02} = 100 \text{ m}\)
(4) Menghitung cepat rambat gelombang
\(v = \lambda \cdot f\)
\(v = 100 \cdot 50\)
\(v = 5.000 \text{ m/s}\)
Soal 05
Gelombang merambat dari A ke B dengan amplitudo 1 cm dan periode 0,2 s. Jarak AB = 0,3 m, cepat rambat gelombang adalah 2,5 m/s. Tentukan beda fase dan beda sudut fase antara A dan B.
Amplitudo (A) = 1 cm = 0,01 meter
Periode (T) = 0,2 s
Frekuensi (f) = \(\dfrac{1}{\text{T}} = \dfrac{1}{0,2} = 5 \text{ Hz}\)
Panjang gelombang dapat dicari dari rumus \(v = \lambda \cdot f\)
\(2, 5 \text{ m/s } = \lambda \cdot 5 \text{ Hz}\)
\(\lambda = \dfrac{2,5}{5} = 0,5 \text{ meter}\)
Beda fase \(\triangle \varphi = \dfrac{\text{jarak AB}}{\text{panjang gelombang}}\)
Beda fase \(\triangle \varphi = \dfrac{0,3}{0,5} = \dfrac{3}{5} = 0,6\)
Beda sudut fase = \(\dfrac{3}{5} \times 2\pi = \dfrac{6}{5}\pi \text{ radian}\)
Soal 06
Salah satu ujung kawat digetarkan harmonik sehingga getaran tersebut merambat ke kanan sepanjang kawat dengan cepat rambat 10 m/s. Ujung kawat mula-mula digetarkan ke atas dengan frekuensi 5 Hz dan amplitudo 0,01 m.
Tentukan:
(A) Persamaan gelombang
(B) Simpangan, kecepatan, dan percepatan partikel di titik \(x = 0,25 \text{ m}\) pada saat ujung kawat telah bergetar 0,1 s.
(C) Sudut fase dan fase gelombang di titik \(x = 0,25 \text{ m}\) pada saat ujung kawat telah bergetar 0,1 s.
(D) Beda fase antara titik \(x = 0,5 \text{ m}\) dan \(x = 0,75 \text{ m}\)
Menghitung panjang gelombang:
\(v = \lambda \cdot f\)
\(10 = \lambda \cdot 5\)
\(\lambda = 2 \text{ meter}\)
Menghitung kecepatan sudut gelombang:
\(\omega = 2\pi f\)
\(\omega = 2\pi (5) = 10 \pi \text{ rad/s}\)
Menghitung bilangan gelombang:
\(k = \dfrac{2\pi}{\lambda}\)
\(k = \dfrac{2\pi}{2} = \pi\)
(A) Menentukan persamaan gelombang
Gelombang merambat ke arah kanan
\(y = 0,01 \sin (10\pi t\:-\:\pi x) \text{ m}\)
(B) Simpangan, kecepatan, dan percepatan partikel di titik \(x = 0,25 \text{ m}\) pada saat ujung kawat telah bergetar 0,1 s.
Simpangan
\(\color{purple} y = 0,01 \sin (10\pi t\:-\:\pi x) \text{ m}\)
Untuk \(x = 0,25 \text{ m}\) dan \(t = 0,1 \text{ s}\)
\(y = 0,01 \sin (10\pi (0,1)\:-\:\pi(0,25)) \text{ m}\)
\(y = 0,01 \sin (\frac{3}{4}\pi) \text{ m}\)
\(y = 0,01 \sin 135^{\circ} \text{ m}\)
\(y = 0,01 (\dfrac{1}{2} \sqrt{2}) \text{ m}\)
\(y = \dfrac{1}{200} \sqrt{2} \text{ m}\)
Kecepatan
\(\color{purple} v = 10\pi \cdot 0,01 \cos (10\pi t\:-\:\pi x) \text{ m/s}\)
Untuk \(x = 0,25 \text{ m}\) dan \(t = 0,1 \text{ s}\)
\(v = 10\pi \cdot 0,01 \cos (10\pi t\:-\:\pi(0,25)) \text{ m/s}\)
\(v = 10\pi \cdot 0,01 \cos (\frac{3}{4}\pi) \text{ m/s}\)
\(v = 0,1 \pi (-\dfrac{1}{2}\sqrt{2}) \text{ m/s}\)
\(v = – \dfrac{1}{20}\sqrt{2} \pi \text{ m/s}\)
Percepatan
\(\color{purple} a = -(10\pi)^2 \cdot 0,01 \sin (10\pi t\:-\:\pi x) \text{ m/s²}\)
Untuk \(x = 0,25 \text{ m}\) dan \(t = 0,1 \text{ s}\)
\(a = -(10\pi)^2 \cdot 0,01 \sin (10\pi (0,1)\:-\:\pi (0,25)) \text{ m/s²}\)
\(a = -100 \pi^2 \cdot 0,01 \sin (\frac{3}{4}\pi) \text{ m/s²}\)
\(a = -\dfrac{1}{2}\sqrt{2} \pi^2 \text{ m/s²}\)
(C) Sudut fase dan fase gelombang di titik \(x = 0,25 \text{ m}\) pada saat ujung kawat telah bergetar 0,1 s.
Sudut fase = \(\omega t \:-\:kx\)
Sudut fase = \(10\pi (0,1) \:-\:\pi (0,25)\)
Sudut fase = \(\dfrac{3}{4}\pi \text{ radian}\)
Fase = \(\dfrac{\text{sudut fase}}{2\pi}\)
Fase = \(\dfrac{\dfrac{3}{4}\pi}{2\pi}\)
Fase = \(\dfrac{3}{8}\)
(D) Beda fase antara titik \(x = 0,5 \text{ m}\) dan \(x = 0,75 \text{ m}\)
\(\triangle \varphi = \dfrac{\triangle x}{\lambda}\)
\(\triangle \varphi = \dfrac{0,75\:-\:0,5}{2}\)
\(\triangle \varphi = \dfrac{1}{8}\)
