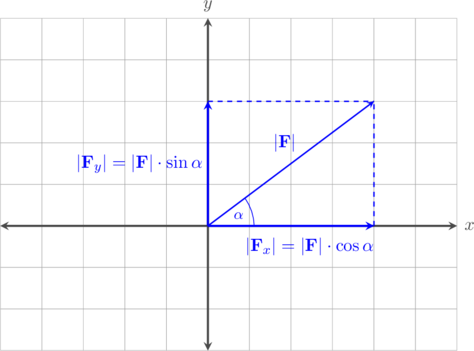
Komponen vektor yang terletak di kuadran I
Vektor \(\textbf {F}\) yang berada di kuadran I dapat digantikan dengan vektor komponen \(\textbf {F}_x\) yang bernilai positif karena arahnya ke kanan dan vektor komponen \(\textbf {F}_y\) yang bernilai positif karena arahnya ke atas.
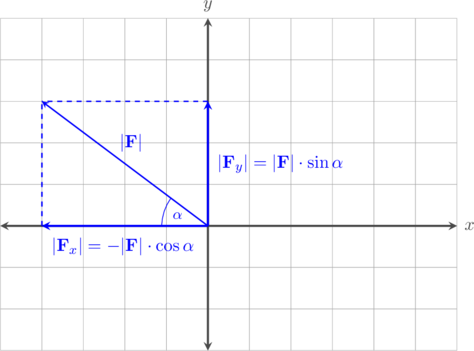
Komponen vektor yang terletak di kuadran II
Vektor \(\textbf {F}\) yang berada di kuadran II dapat digantikan dengan vektor komponen \(\textbf {F}_x\) yang bernilai negatif karena arahnya ke kiri dan vektor komponen \(\textbf {F}_y\) yang bernilai positif karena arahnya ke atas.
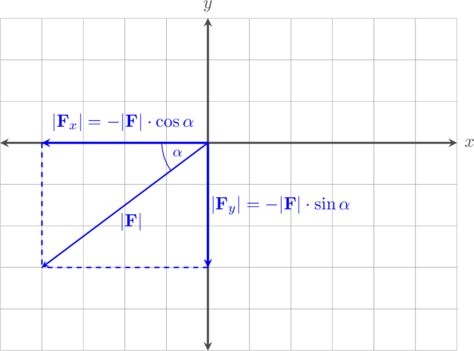
Komponen vektor yang terletak di kuadran III
Vektor \(\textbf {F}\) yang berada di kuadran III dapat digantikan dengan vektor komponen \(\textbf {F}_x\) yang bernilai negatif karena arahnya ke kiri dan vektor komponen \(\textbf {F}_y\) yang bernilai negatif karena arahnya ke bawah.
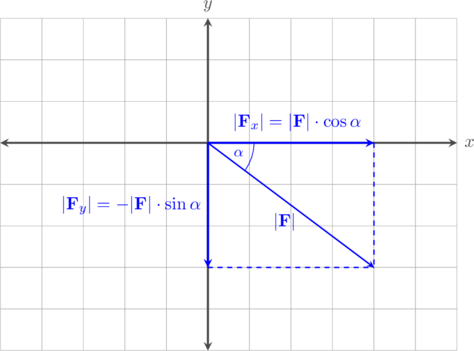
Komponen vektor yang terletak di kuadran IV
Vektor \(\textbf {F}\) yang berada di kuadran IV dapat digantikan dengan vektor komponen \(\textbf {F}_x\) yang bernilai positif karena arahnya ke kanan dan vektor komponen \(\textbf {F}_y\) yang bernilai negatif karena arahnya ke bawah.
Sudut Istimewa
| $$0^{\circ}$$ | $$30^{\circ}$$ | $$37^{\circ}$$ | $$45^{\circ}$$ | $$53^{\circ}$$ | $$60^{\circ}$$ | $$90^{\circ}$$ | |
| sin | $$0$$ | $$\dfrac{1}{2}$$ | $$\dfrac{3}{5}$$ | $$\dfrac{1}{2}\sqrt{2}$$ | $$\dfrac{4}{5}$$ | $$\dfrac{1}{2}\sqrt{3}$$ | $$1$$ |
| cos | $$1$$ | $$\dfrac{1}{2}\sqrt{3}$$ | $$\dfrac{4}{5}$$ | $$\dfrac{1}{2}\sqrt{2}$$ | $$\dfrac{3}{5}$$ | $$\dfrac{1}{2}$$ | $$0$$ |
| tan | $$0$$ | $$\dfrac{1}{3}\sqrt{3}$$ | $$\dfrac{3}{4}$$ | $$1$$ | $$\dfrac{4}{3}$$ | $$\sqrt{3}$$ | $$\infty$$ |
CONTOH SOAL
Soal 1
Diketahui 3 buah vektor \(\textbf {a}, \textbf {b}, \text{ dan } \textbf {c}\) yang masing-masing panjangnya 10 m, 5 m, dan 8 m. Vektor \(\textbf {a}\) membentuk sudut \(53^{\circ}\) terhadap sumbu x, dan vektor \(\textbf {b}\) membentuk sudut \(37^{\circ}\) terhadap sumbu x. Tentukan besar dan arah resultan ketiga vektor tersebut.
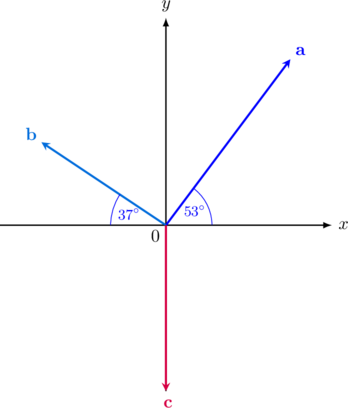
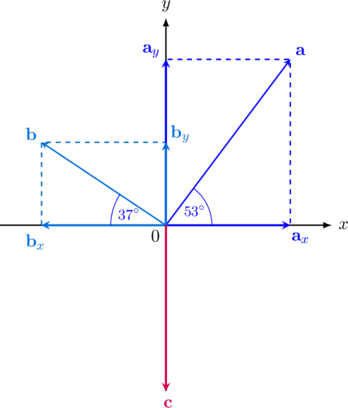
| Vektor | Komponen di Sumbu X (Rx) | Komponen di Sumbu Y (Ry) |
| $\textbf {a}$ | \(|\textbf {a}_x| = |\textbf {a}|\cdot \cos 53^{\circ}\)
\(|\textbf {a}_x| = 10\cdot 0,6 = 6\text{ m}\) |
\(|\textbf {a}_y| = |\textbf {a}|\cdot \sin 53^{\circ}\)
\(|\textbf {a}_y| = 10\cdot 0,8 = 8\text{ m}\) |
| $\textbf {b}$ | \(|\textbf {b}_x| = -|\textbf {b}|\cdot \cos 37^{\circ}\)
\(|\textbf {a}_x| = -5\cdot 0,8 = -4\text{ m}\) |
\(|\textbf {b}_y| = |\textbf {b}|\cdot \sin 37^{\circ}\)
\(|\textbf {a}_x| = 5\cdot 0,6 = 3\text{ m}\) |
| $\textbf {c}$ | \(0\text{ m}\) | \(-8 \text{ m}\) |
| Total | \(2 \text{ m}\) | \(3 \text{ m}\) |
\begin{equation*}
\begin{split}
|\textbf {R}| &= \sqrt{(|\textbf {R}_x|)^2 + (|\textbf {R}_y|)^2}\\\\
|\textbf {R}| &= \sqrt{2^2 + 3^2}\\\\
|\textbf {R}| &= \sqrt{4 + 9}\\\\
|\textbf {R}| &= \sqrt{13}\text{ m}
\end{split}
\end{equation*}
Vektor resultannya terletak di kuadran I karena nilai Rx positif dan Ry positif.
Besar resultan vektornya adalah \(\sqrt{13}\) m
\begin{equation*}
\begin{split}
\tan \alpha &= \dfrac{|\textbf {R}_y|}{|\textbf {R}_x|}\\\\
\tan \alpha &= \dfrac{3}{2} = 1,5\\\\
\alpha& = \tan^{-1} 1,5 = 56,3^{\circ}
\end{split}
\end{equation*}
Vektor resultannya memiliki arah \(56,3^{\circ}\) diukur dari sumbu x positif berlawanan arah dengan jarum jam
Soal 2
Diketahui:
Vektor \(\text{F}_1 = 20 \text{ N}\) dengan arah \(120^{\circ}\)
Vektor \(\text{F}_2 = 40 \text{ N}\) dengan arah \(180^{\circ}\)
Vektor \(\text{F}_3 = 40 \text{ N}\) dengan arah \(300^{\circ}\)
Tentukan besar dan arah resultan ketiga vektor tersebut
Menggambar posisi masing-masing vektor, dengan arah sudut diukur dari sumbu \(x\) positif berlawanan arah dengan jarum jam
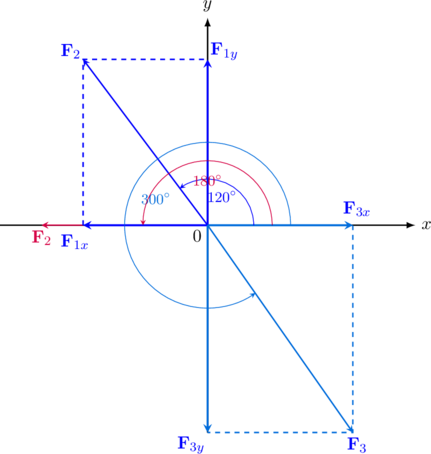
Pilih sudut lancip untuk setiap vektor yang menempel pada sumbu \(x\)
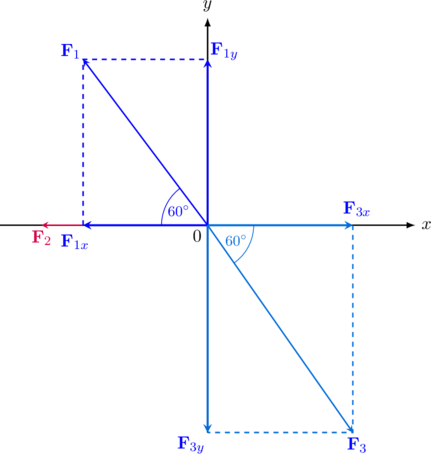
| Vektor | Komponen di Sumbu X (Rx) | Komponen di Sumbu Y (Ry) |
| ${\textbf{F}_1}$ | \(|\textbf{F}_{1x}| = -|\textbf{F}_1|\cdot \cos 60^{\circ}\)
\(|\textbf{F}_{1x}| = -20\cdot \frac{1}{2} = -10\text{ N}\) |
\(|\textbf{F}_{1y}| = |\textbf{F}_1|\cdot \sin 60^{\circ}\)
\(|\textbf{F}_{1y}| = 20\cdot \frac{1}{2}\sqrt{3} = 10\sqrt{3}\text{ N}\) |
| $ {\textbf{F}_2}$ | \(-40 \text{ N}\) | \(0 \text{ N}\) |
| ${\textbf{F}_3}$ | \(|\text{F}_{3x}| = |\text{F}_3|\cdot \cos 60^{\circ}\)
\(|\textbf{F}_{3x}| = 40\cdot \frac{1}{2} = 20\text{ N}\) |
\(|\text{F}_{3y}| = -|\text{F}_3|\cdot \sin 60^{\circ}\)
\(|\textbf{F}_{3y}| = -40\cdot \frac{1}{2}\sqrt{3} = -20\sqrt{3}\text{ N}\) |
| Total | \(-30 \text{ N}\) | \(-10\sqrt{3} \text{ N}\) |
\begin{equation*}
\begin{split}
|\textbf{R}| &= \sqrt{(|\textbf {R}_x|)^2 + (|\textbf{R}_y|)^2}\\\\
|\textbf{R}| &= \sqrt{(-30)^2 + (-10\sqrt{3})^2}\\\\
|\textbf{R}| &= \sqrt{900 + 300}\\\\
|\textbf{R}| &= \sqrt{1200}\text{ N}\\\\
|\textbf{R}| &= 20\sqrt{3}\text{ N}
\end{split}
\end{equation*}
Vektor resultannya terletak di kuadran III karena nilai Rx negatif dan Ry negatif.
Besar resultan vektornya adalah \(20\sqrt{3}\text{ N}\)
\begin{equation*}
\begin{split}
\tan \alpha &= \dfrac{|\textbf{R}_y|}{|\textbf{R}_x|}\\\\
\tan \alpha &= \dfrac{-10\sqrt{3} }{-30} = \dfrac{1}{3}\sqrt{3}\\\\
\alpha& = \tan^{-1} \dfrac{1}{3}\sqrt{3} = 180^{\circ} + 30^{\circ} = 210^{\circ}\\\\
\end{split}
\end{equation*}
Sudut terletak di kuadran III
Vektor resultannya memiliki arah 210° diukur dari sumbu x positif berlawanan arah dengan jarum jam
