Halo, teman-teman! Saat ini kita akan belajar tentang persamaan regresi linear sederhana. Topik ini sangat penting dalam statistika karena membantu kita memahami hubungan antara dua variabel dan membuat prediksi berdasarkan data yang ada.
Apa itu regresi linear sederhana?
Regresi linear sederhana adalah metode statistik yang digunakan untuk melihat hubungan antara dua variabel:
- Variabel independen (X): variabel yang mempengaruhi (disebut juga prediktor)
- Variabel dependen (Y): variabel yang dipengaruhi (disebut juga respon)
Secara matematis, regresi linear sederhana dinyatakan dengan persamaan:
$$\bbox[white, 5px, border: 2px solid red] {y = a + bx}$$
di mana:
- \(y\) = nilai prediksi dari variabel dependen
- \(x\) = nilai dari variabel independen
- \(a\) = intercept (nilai Y ketika X = 0)
- \(b\) = koefisien regresi (kemiringan garis, menunjukkan perubahan Y untuk setiap kenaikan satu satuan X)
Langkah-Langkah Menggambar Garis Regresi Linear
(1) Menghitung \(\overline{X}\) dan \(\overline{Y}\)
$$\bbox[white, 5px, border: 2px solid red] {\overline{X} = \dfrac{\displaystyle\sum\limits_{i=1}^n x_i}{n}}$$
$$\bbox[white, 5px, border: 2px solid red] {\overline{Y} =\dfrac{\displaystyle\sum\limits_{i=1}^n y_i}{n}}$$
(2) Menghitung \(S_{xy}\) dan \(S_{xx}\)
$$\bbox[white, 5px, border: 2px solid red] {S_{xy} = \displaystyle\sum\limits_{i=1}^n {x_i y_i} \:-\: \dfrac{\displaystyle\sum\limits_{i=1}^n {x_i} \cdot \displaystyle\sum\limits_{i=1}^n {y_i}}{n} }$$
$$\bbox[white, 5px, border: 2px solid red] {S_{xx} = \displaystyle\sum\limits_{i=1}^n {x_i^2} \:-\: \dfrac{\left(\displaystyle\sum\limits_{i=1}^n {x_i}\right)^2 }{n} }$$
(3) Menghitung nilai \(b\)
$$\bbox[white, 5px, border: 2px solid red] {b = \dfrac{S_{xy}}{S_{xx}}}$$
(4) Menghitung nilai \(a\)
$$\bbox[white, 5px, border: 2px solid red] {a = \overline {Y}\:-\:b \overline{X}}$$
(5) Menyusun Persamaan Garis Regresi
$$\bbox[white, 5px, border: 2px solid red] {y = a + bx}$$
(7) Menggambar Garis Regresi
Contoh:
Seorang guru ingin mengetahui hubungan antara jumlah jam belajar (X) dan nilai ujian (Y). Berikut datanya:
| Jam Belajar (X) | Nilai Ujian (Y) |
|---|---|
| 2 | 65 |
| 4 | 70 |
| 6 | 75 |
| 8 | 80 |
| 10 | 85 |
Penyelesaian:
\(\displaystyle\sum\limits_{i=1}^5 x_i = 2 + 4 + 6 + 8 + 10 = 30\)
\(\displaystyle\sum\limits_{i=1}^5 y_i = 65 + 70 + 75 + 80 + 85 = 375\)
\(\displaystyle\sum\limits_{i=1}^5 x_i^2 = 2^2 + 4^2 + 6^2 + 8^2 + 10^2 = 220\)
\(\displaystyle\sum\limits_{i=1}^5 x_i\cdot y_i = 2(65) + 4(70) + 6(75) + 8(80) + 10(85) = 2350\)
(1) Menghitung \(\overline{X}\) dan \(\overline{Y}\)
\(\overline{X} = \dfrac{\displaystyle\sum\limits_{i=1}^5 x_i}{5} = \dfrac{30}{5} = 6\)
\(\overline{Y} =\dfrac{\displaystyle\sum\limits_{i=1}^5 y_i}{5} = \dfrac{375}{5} = 75\)
(2) Menghitung \(S_{xy}\) dan \(S_{xx}\)
\(S_{xy} = \displaystyle\sum\limits_{i=1}^5 {x_i y_i} \:-\: \dfrac{\displaystyle\sum\limits_{i=1}^5 {x_i} \cdot \displaystyle\sum\limits_{i=1}^5 {y_i}}{5}\)
\(S_{xy} = 2350\:-\: \dfrac{30 \cdot 375}{5}\)
\(S_{xy} = 2350\:-\: 2250\)
\(S_{xy} = 100\)
\(S_{xx} = \displaystyle\sum\limits_{i=1}^5 {x_i^2} \:-\: \dfrac{\left(\displaystyle\sum\limits_{i=1}^5 {x_i}\right)^2 }{5}\)
\(S_{xx} = 220\:-\: \dfrac{30^2 }{5}\)
\(S_{xx} = 220\:-\: 180\)
\(S_{xx} = 40\)
(3) Menghitung nilai \(b\)
\(b = \dfrac{S_{xy}}{S_{xx}}\)
\(b = \dfrac{100}{40} = 2,5\)
(4) Menghitung nilai \(a\)
\(a = \overline {Y}\:-\:b \overline{X}\)
\(a = 75\:-\:2,5 (6)\)
\(a =60\)
(5) Menyusun Persamaan Garis Regresi
\(y = a + bx\)
\(y= 60 + 2,5x\)
(6) Menggambar Garis Regresi
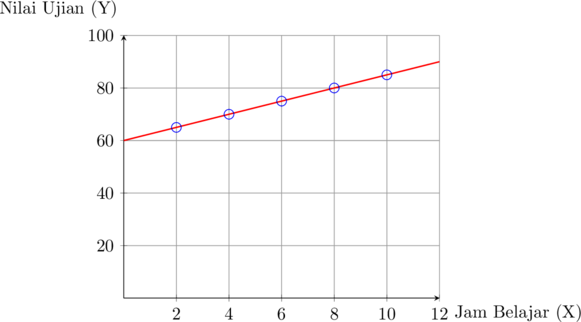
Untuk menggambar garis \(y= 60 + 2,5x\) di dalam diagram Cartesius butuh minimal 2 buah titik yang dilalui oleh garis tersebut.
Untuk \(x = 0 \rightarrow y = 60 + 2,5(0) = 60\) titik pertama koordinatnya (0, 60)
Untuk \(x = 4 \rightarrow y = 60 + 2,5(4) = 70\) titik pertama koordinatnya (4, 70)
Garis \(y= 60 + 2,5x\) didapatkan dengan menghubungkan titik (0, 60) dan (4, 70), buat juga perpanjangan garisnya.
Garis Regresi Linear