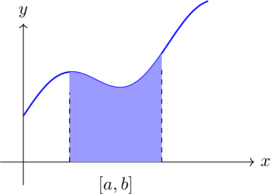
Luas daerah di bawah kurva \(f(x)\) yang dibatasi sumbu-\(x\) dari \(x = a\) sampai \(x = b\) dapat dihitung menggunakan integral tertentu.
\[L = \int_a^b f(x) \, dx\]
SOAL 1
Tentukan luas daerah yang dibatasi kurva \(y = x(x+1)(x-2)\) dan sumbu \(x\)

Persamaan kurva \(y = x(x+1)(x-2) = x^3-x^2-2x\)
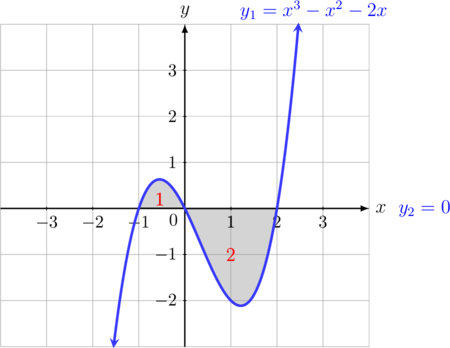
\(\text{Luas daerah}= \text{Luas 1 + Luas 2}\)
\(\int_{-1}^{0} (y_1 \:-\: y_2)\text{ dx} + \int_{0}^{2} (y_2 \:-\: y_1) \text{ dx}\)
\(\int_{-1}^{0} (x^3\:-\:x^2-2x) \:-\: 0\text{ dx} + \int_{0}^{2} 0 \:-\: (x^3-x^2-2x) \text{ dx}\)
\(\left.(\frac{1}{4}x^4\:-\:\frac{1}{3}x^3\:-\:x^2)\right |_{-1}^0 \:-\:\left.(\frac{1}{4}x^4\:-\:\frac{1}{3}x^3\:-\:x^2)\right |_0^2\)
\(0\:-\:(\frac{1}{4}(-1)^4\:-\:\frac{1}{3}(-1)^3\:-\:(-1)^2)\:-\:(\frac{1}{4}(2)^4-\frac{1}{3}(2)^3-(2)^2 – 0)\)
\(-\frac{1}{4}\:-\:\frac{1}{3}+1+\frac{8}{3}\)
\(\frac{-3\:-\:4+12+32}{12}\)
\(\frac{37}{12}\text{ satuan luas}\)
SOAL 2
Tentukan luas daerah yang diarsir berikut:
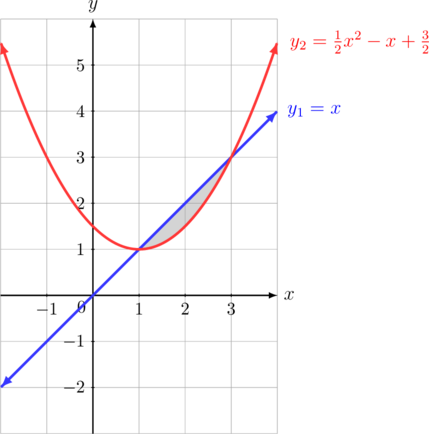
Kedua kurva berpotongan di titik (1, 1) dan (3, 3)
Luas daerah yang diarsir = \(\int_{1}^{3} (y_1 \:-\: y_2) \text{ dx }\)
\(\int_{1}^{3} x \:-\: (\frac{1}{2}x^2 \:-\: x + \frac{3}{2}) \text{ dx }\)
\(\int_{1}^{3} (-\frac{1}{2}x^2 + 2x \:-\:\frac{3}{2}) \text{ dx }\)
\(\left.-\frac{1}{6}x^3 + x^2\:-\: \frac{3}{2}x \right |_1^3\)
\( -\frac{1}{6}(3)^3 + 3^2\:-\: \frac{3}{2}(3) \:-\: (-\frac{1}{6}(1)^3 + (1)^2- \frac{3}{2}(1))\)
\( -\frac{27}{6} + 9 \:-\: \frac{9}{2} \:-\: ( -\frac{1}{6} + 1 \:-\: \frac{3}{2})\)
\( -\frac{27}{6} + 9 \:-\: \frac{9}{2} + \frac{1}{6} \:-\: 1 + \frac{3}{2}\)
\( -\frac{13}{3} + 5\)
\( \frac{2}{3}\)
\(\frac{2}{3}\text{ satuan luas}\)
SOAL 3
Tentukan luas daerah yang diarsir berikut:
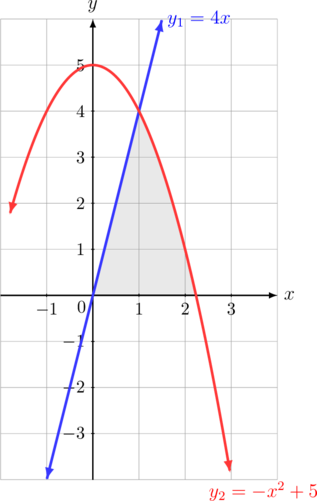
Kedua fungsi berpotongan di titik (1, 4)
Titik potong kurva \(y_2 = -x^2 + 5\) terhadap sumbu \(x\) didapat jika \(y = 0\)
\(0 = -x^2 + 5\)
\(-x^2 =- 5\)
\(x^2 = 5\)
\(x= \pm \sqrt{5}\)
Titik potong kurva \(y_2\) terhadap sumbu \(x\) berada di \((-\sqrt{5}, 0) \text{ dan } (\sqrt{5}, 0)\)
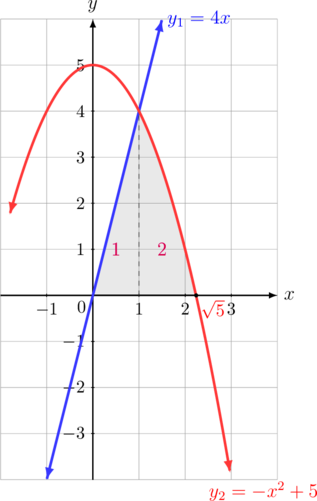
\(\text{Luas daerah}= \text{Luas 1 + Luas 2}\)
\(\int_{0}^{1} y_1 \text{ dx} + \int_{1}^{\sqrt{5}} y_2 \text{ dx}\)
\(\int_{0}^{1} 4x \text{ dx} + \int_{1}^{\sqrt{5}}(-x^2 + 5) \text{ dx}\)
\(\left.\frac{4}{2}x^2\right |_0^1 + \left.(-\frac{1}{3}x^3 + 5x)\right |_1^{\sqrt{5}}\)
\(2 + (-\frac{1}{3}(\sqrt{5})^3 + 5\sqrt{5}) \:-\: (-\frac{1}{3}(1)^3 + 5)\)
\(2 + (-\frac{5}{3}\sqrt{5} + 5\sqrt{5})\:-\: \frac{14}{3}\)
\(2 + \frac{10}{3}\sqrt{5} \:-\: \frac{14}{3}\)
\(\frac{10}{3}\sqrt{5} \:-\: \frac{8}{3}\text{ satuan luas}\)
