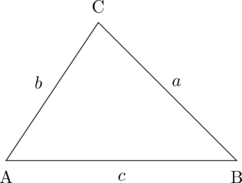
\(a\) adalah sisi di depan sudut A
\(b\) adalah sisi di depan sudut B
\(c\) adalah sisi di depan sudut C
Aturan cosinus yang berlaku pada segitiga ABC adalah:
\(\color{blue} a^2 = b^2 + c^2 \:-\:2\cdot b \cdot c \cdot \cos \text{A}\)
\(\color{blue} b^2 = a^2 + c^2 \:-\:2\cdot a \cdot c \cdot \cos \text{B}\)
\(\color{blue} c^2 = a^2 + b^2 \:-\:2\cdot a \cdot b \cdot \cos \text{C}\)
Persamaan di atas, dapat juga ditulis sebagai berikut:
\(\color{blue} \cos \text{A} = \dfrac{b^2 + c^2\:-\:a^2}{2\cdot b \cdot c}\)
\(\color{blue} \cos \text{B} = \dfrac{a^2 + c^2\:-\:b^2}{2\cdot a \cdot c}\)
\(\color{blue} \cos \text{C} = \dfrac{a^2 + b^2\:-\:c^2}{2\cdot a\cdot b}\)
Panjang sisi BC = \(a\)
\(a^2 = b^2 + c^2 \:-\:2\cdot b \cdot c \cdot \cos \text{A}\)
\(a^2 = 4^2 + 6^2 \:-\:2\cdot 4 \cdot 6 \cdot \cos 120^{\circ}\)
\(a^2 = 16 + 36 \:-\:2\cdot 24 \cdot \cos (180^{\circ}\:-\:60^{\circ})\)
\(a^2 = 52 \:-\:2\cdot 24 \cdot (-\cos 60^{\circ})\)
\(a^2 = 52 + \cancel{2}\cdot 24 \cdot \frac{1}{\cancel{2}}\)
\(a^2 = 52 + 24\)
\(a^2 = 76\)
\(a = \sqrt{76}\)
\(a = 2\sqrt{19}\)
Jadi, panjang sisi BC adalah \(2\sqrt{19}\)
Panjang sisi AC = \(b\)
\(a^2 = b^2 + c^2 \:-\:2\cdot b \cdot c \cdot \cos \text{A}\)
\((5\sqrt{3})^2 = b^2 + 10^2 \:-\:2\cdot b \cdot 10 \cdot \cos 60^{\circ}\)
\((5\sqrt{3})^2 = b^2 + 10^2 \:-\:2\cdot b \cdot 10 \cdot \cos 60^{\circ}\)
\(75 = b^2 + 100\:-\:\cancel{2}\cdot b \cdot 10 \cdot \frac{1}{\cancel{2}}\)
\(75 = b^2 + 100\:-\:10b\)
\(0 = b^2\:-\:10b + 25\)
\(0 = (b\:-\:5)^2\)
\(b\:-\:5 = 0\)
\(b = 5\)
Jadi, panjang sisi AC adalah 5
\(\cos \text{C} = \dfrac{a^2 + b^2\:-\:c^2}{2\cdot a\cdot b}\)
\(\cos \text{C} = \dfrac{(4\sqrt{2})^2 + 3^2\:-\:(\sqrt{65})^2}{2\cdot 4\sqrt{2}\cdot 3}\)
\(\cos \text{C} = \dfrac{32 + 9\:-\:65}{24\sqrt{2}}\)
\(\cos \text{C} = \dfrac{-\cancel{24}}{\cancel{24}\sqrt{2}}\)
\(\cos \text{C} = -\dfrac{1}{\sqrt{2}}\)
\(\cos \text{C} = -\dfrac{1}{2}\sqrt{2}\)
Karena nilai cosinus negatif, artinya C berada di kuadran II
\(\text{C} = 180^{\circ}\:-\:45^{\circ}\)
\(\text{C} = 135^{\circ}\)
Jadi, besar sudut C adalah 135°
Langkah 1: menghitung panjang BD
Perhatikan segitiga ABD
\(\text{BD}^2 = \text{AB}^2 + \text{AD}^2\:-\:2\cdot \text{AB} \cdot \text{AD}\cdot \cos 30^{\circ}\)
\(\text{BD}^2 = (4\sqrt{3})^2 + 3^2\:-\:2\cdot 4\sqrt{3}\cdot 3\cdot \frac{1}{2}\sqrt{3}\)
\(\text{BD}^2 = 48 + 9\:-\:\cancel{2}\cdot 4\sqrt{3}\cdot 3\cdot \frac{1}{\cancel{2}}\sqrt{3}\)
\(\text{BD}^2 = 57\:-\:36\)
\(\text{BD}^2 = 21\)
\(\text{BD} = \sqrt{21}\)
Langkah 2: menghitung panjang BC
Perhatikan segitiga BCD
\(\text{BD}^2 = \text{BC}^2 + \text{CD}^2\:-\:2\cdot \text{BC} \cdot \text{CD}\cdot \cos 120^{\circ}\)
\(21 = \text{BC}^2 + 1^2\:-\:2\cdot \text{BC} \cdot 1\cdot \cos (180^{\circ}\:-\:60^{\circ})\)
\(21 = \text{BC}^2 + 1^2\:-\:2\cdot \text{BC} \cdot 1\cdot (-\cos 60^{\circ})\)
\(21 = \text{BC}^2 + 1 + \cancel{2}\cdot \text{BC} \cdot 1\cdot \frac{1}{\cancel{2}}\)
\(21 = \text{BC}^2 + 1 + \text{BC}\)
\(0 = \text{BC}^2 + \text{BC} + 1 \:-\:21\)
\(0 = \text{BC}^2 + \text{BC} \:-\:20\)
\(0 = (\text{BC} + 5)(\text{BC}\:-\:4)\)
\(\text{BC}\:-\:4 = 0\)
\(\text{BC} = 4\)
Jadi, panjang sisi BC adalah 4
