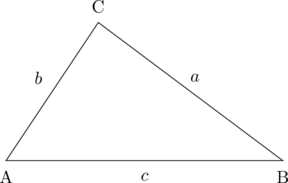
Luas segitiga ABC, dapat dihitung dengan rumus:
\(\color{blue} \text{L} = \dfrac{1}{2}\cdot a \cdot b \cdot \sin \text{C}\)
\(\color{blue} \text{L} = \dfrac{1}{2}\cdot b \cdot c \cdot \sin \text{A}\)
\(\color{blue} \text{L} = \dfrac{1}{2}\cdot a \cdot c \cdot \sin \text{B}\)
CONTOH SOAL
SOAL 1
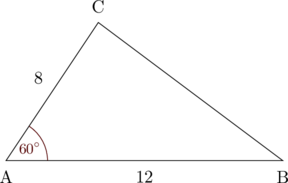
Tentukan luas segitiga ABC di atas.
\(\text{L} = \dfrac{1}{2}\cdot b \cdot c \cdot \sin \text{A}\)
\(\text{L} = \dfrac{1}{2}\cdot 8 \cdot 12 \cdot \sin 60^{\circ}\)
\(\text{L} = \dfrac{1}{\cancel{2}}\cdot \cancelto{4}{8} \cdot \cancelto{6}{12} \cdot \dfrac{1}{\cancel{2}}\sqrt{3}\)
\(\text{L} = 24\sqrt{3}\text{ satuan luas}\)
SOAL 2

Tentukan luas segitiga ABC di atas.
Langkah 1: gunakan aturan cosinus untuk menghitung panjang sisi BC
Mulailah menulis rumus dari sisi yang berada di depan sudut yang diketahui
\(b^2 = a^2 + c^2 \:-\:2\cdot a \cdot c \cdot \cos \text{B}\)
\((5\sqrt{3})^2 = a^2 + (10\sqrt{3})^2 \:-\:2\cdot a \cdot 10\sqrt{3} \cdot \cos 30^{\circ}\)
\(75 = a^2 + 300 \:-\:\cancel{2}\cdot a \cdot 10\sqrt{3} \cdot \frac{1}{\cancel{2}}\sqrt{3}\)
\(75 = a^2 + 300 \:-\:30a\)
\(0 = a^2 \:-\:30a + 300 \:-\:75\)
\(0 = a^2 \:-\:30a + 225\)
\(0 = (a \:-\:15)^2\)
\(a\:-\:15 = 0\)
\(a = 15\)
Panjang sisi BC = 15
Langkah 2: menghitung luas segitiga ABC
\(\text{L} = \dfrac{1}{2}\cdot a \cdot c \cdot \sin \text{B}\)
\(\text{L} = \dfrac{1}{2}\cdot 15 \cdot 10\sqrt{3} \cdot \sin 30^{\circ}\)
\(\text{L} = \dfrac{1}{2}\cdot 15 \cdot 10\sqrt{3} \cdot \dfrac{1}{2}\)
\(\text{L} = \dfrac{1}{4}\cdot 150\sqrt{3}\)
\(\text{L} = \dfrac{75}{2}\sqrt{3}\text{ satuan luas}\)
SOAL 3
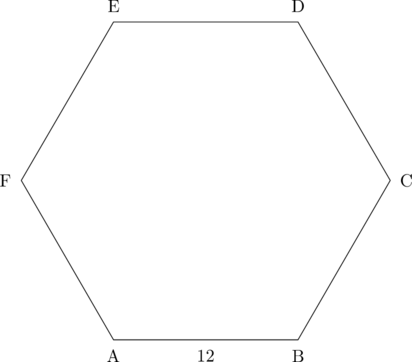
Tentukan luas segi enam beraturan di atas.

Karena besar sudut pusat segi enam beraturan adalah \(\dfrac{360^{\circ}}{6} = 60^{\circ}\), maka segitiga AOB yang terbentuk adalah segitiga sama sisi.
Luas segi enam beraturan = 6 × luas segitiga AOB
\(\text{L} = 6 \times \dfrac{1}{2}\cdot \text{AO}\cdot \text{BO} \cdot \sin 60^{\circ}\)
\(\text{L} = 6 \times \dfrac{1}{2}\cdot 12 \cdot 12 \cdot \sin 60^{\circ}\)
\(\text{L} = 6 \times \dfrac{1}{\cancel{2}}\cdot \cancelto{6}{12} \cdot \cancelto{6}{12} \cdot \dfrac{1}{\cancel{2}}\sqrt{3}\)
\(\text{L} = 216\sqrt{3}\text{ satuan luas}\)
Jadi, luas segi enam di atas adalah \(216\sqrt{3}\text{ satuan luas}\)
