KUBUS
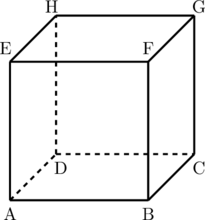
Kubus ABCD.EFGH memiliki 6 buah sisi yang berbentuk persegi dan 12 buah rusuk.
Volume kubus = \(s^3\)
Luas permukaan kubus = \(6\cdot s^2\)
Luas permukaan kubus tanpa tutup = \(5 \cdot s^2\)
Menentukan panjang diagonal bidang/sisi kubus
Diagonal sisi kubus: AF, BE, BG, CF, CH, DG, AH, DE, AC, BD, EG, HF (12 buah)
Panjang diagonal sisi kubus = \(s\sqrt{2}\)
Menentukan panjang diagonal ruang kubus
Diagonal ruang kubus: AG, CE, HB, DF (4 buah)
Panjang diagonal ruang = \(s\sqrt{3}\)
BALOK
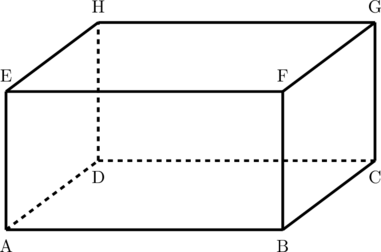
Balok ABCD.EFGH memiliki panjang \(p\), lebar \(l\), dan tinggi \(t\).
Volume balok = \(p \times l \times t\)
Luas permukaan balok = \(2(p\cdot l + p \cdot t + l \cdot t)\)
Luas permukaan balok tanpa tutup = \(p \cdot l + 2p\cdot t + 2l\cdot t\)
Menentukan panjang diagonal sisi AF
Perhatikan segitiga siku-siku ABF
AF dapat dihitung menggunakan rumus pythagoras, \(\textbf{AF}^2 = \textbf{AB}^2 + \textbf{BF}^2\)
Menentukan panjang diagonal ruang AG
Perhatikan segitiga siku-siku ACG
AG dapat dihitung menggunakan rumus pythagoras, \(\textbf{AG}^2 = \textbf{AC}^2 + \textbf{CG}^2\)
PRISMA
Prisma adalah bangun ruang tiga dimensi yang dibatasi oleh alas dan tutup identik berbentuk segi-n dan sisi-sisi tegak berbentuk persegi atau persegi panjang.
(sumber: Prisma (geometri) – Wikipedia bahasa Indonesia, ensiklopedia bebas)
Gambar prisma segi enam
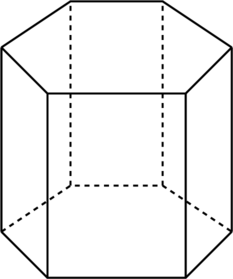
Volume prisma = luas alas × tinggi prisma
Luas permukaan prisma = (2 × luas alas) + (keliling alas × tinggi prisma)
LIMAS
Gambar limas segi empat

Sisi tegak limas berbentuk segitiga, yaitu TAB, TBC, TDC, TAD.
\(\textbf{Volume limas} = \dfrac{1}{3} \times \textbf{ luas alas } \times \textbf{ tinggi}\)
\(\textbf{Luas permukaan limas} = \textbf{ luas alas } + \textbf{semua luas sisi tegak}\)
Cara menentukan luas sisi tegak limas
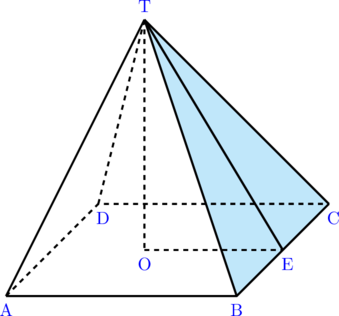
Tinggi limas = TO
Garis pelukis limas = TE
Perhatikan segitiga siku-siku TOE
\(\color{blue} \textbf{TE}^2 = \textbf{TO}^2 + \textbf{OE}^2\)
Luas sisi tegak TBC = \(\color{blue}\dfrac{1}{2} \times \textbf{BC} \times \textbf{TE}\)
