Bagian-Bagian Kerucut
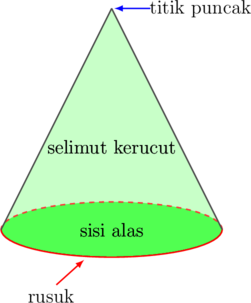
• Jumlah rusuk kerucut = 1 buah
• Jumlah sisi kerucut = 2 buah, terdiri dari 1 buah sisi alas yang berbentuk lingkaran dan 1 buah sisi lengkung (selimut kerucut)
• Jumlah titik sudut = 1
Volume dan Luas Permukaan Kerucut
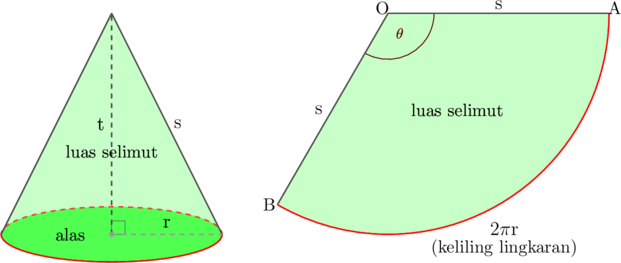
Volume kerucut = \(\frac{1}{3}\times \text{ luas alas } \times \text{ tinggi}\)
Volume kerucut = \(\frac{1}{3}\cdot\pi r^2 \cdot t\)
Setelah kerucut dibuka, luas selimut kerucut sama dengan luas juring yang terbentuk dan panjang busur yang terbentuk sama dengan keliling alas kerucut yang berbentuk lingkaran
\(\dfrac{\text{Luas juring}}{\text{Panjang busur}} = \dfrac{\frac{\theta}{360^\circ}\cdot \pi s^2}{\frac{\theta}{360^\circ}\cdot 2\pi s}\)
\(\dfrac{\text{Luas selimut kerucut}}{2\pi r} = \dfrac{\cancel{\frac{\theta}{360^\circ}}\cdot \cancel{\pi} s^2}{\cancel{\frac{\theta}{360^\circ}}\cdot 2 \cancel{\pi} s}\)
\(\text{Luas selimut kerucut} = \pi r s\), dengan \(s\) adalah garis pelukis
Hubungan antara jari-jari, tinggi kerucut, dan panjang garis pelukis adalah sebagai berikut:
\(r^2 + t^2 = s^2\)
Luas permukaan kerucut = luas alas + luas selimut
Luas permukaan kerucut = \(\pi r^2 + \pi r s\)
Luas permukaan kerucut = \(\pi r(r + s)\)
CONTOH SOAL
Soal 1
Sebuah kerucut memiliki jari-jari alas 7 cm dan tinggi 24 cm, tentukan:
a. Volume kerucut
b. Luas selimut kerucut
c. Luas permukaan kerucut
\(\frac{1}{3}\cdot \frac{22}{7} \cdot 7^2 \cdot 24\)
\(\frac{1}{3}\cdot \frac{22}{7} \cdot 7^2 \cdot 24\)
\(1232 \text{ cm}^3\)
b. Luas selimut kerucut = \(\pi r s\)
s adalah garis pelukis
\(r^2 + t^2 = s^2\)
\(7^2 + 24^2 = s^2\)
\(49 + 576 = s^2\)
\( s^2 = 625\)
\( s = \sqrt{625} = 25 \text{ cm}\)
Luas selimut kerucut = \(\frac{22}{7}\cdot 7 \cdot 25\)
Luas selimut kerucut = 550 cm²
c. Luas permukaan kerucut = \(\pi r(r + s)\)
\(\frac{22}{7}\cdot 7 (7 + 25)\)
\(22 \cdot 32\)
704 cm²
Soal 2
Sebuah kerucut memiliki panjang garis pelukis 20 cm dan tinggi 16 cm, tentukan:
a. Panjang jari-jari kerucut
b. Luas permukaan kerucut
c. Volume kerucut
a. Gunakan rumus Pythagoras untuk mencari panjang jari-jari kerucut
\(r^2 + t^2 = s^2\)
\(r^2 + 16^2 = 20^2\)
\(r^2 + 256 = 400\)
\(r^2 = 400 – 256\)
\(r^2 = 144\)
\(r = \sqrt{144} = 12 \text{ cm}\)
b. Luas permukaan kerucut = \(\pi r(r + s)\)
\(\frac{22}{7}\cdot 12 (12 + 20)\)
\(\frac{22}{7}\cdot 12 (32)\)
\(\frac{8448}{7}\)
1206,86 cm²
c. Volume kerucut = \(\frac{1}{3}\cdot\pi r^2 \cdot t\)
\(\frac{1}{3}\cdot \frac{22}{7} \cdot 12^2 \cdot 16\)
\(\frac{1}{3}\cdot \frac{22}{7} \cdot 2304\)
\(\frac{50688}{21}\)
2413,71 cm³
Soal 3
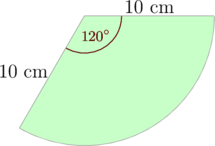
Sebuah pola kertas berbentuk juring lingkaran dengan sudut pusat 120° dan jari-jari 10 cm akan dibuat menjadi sebuah kerucut. Tentukan:
a. Luas selimut kerucut
b. Tinggi kerucut yang terbentuk
c. Volume kerucut yang terbentuk
a. Luas selimut kerucut = luas juring lingkaran
Luas selimut kerucut = \(\frac{120^\circ}{360^\circ}\cdot \pi R^2\)
Luas selimut kerucut = \(\frac{1}{3}\cdot 3,14 \cdot 10^2\)
Luas selimut kerucut = \(\frac{314}{3} = 104,67 \text{ cm}^2\)
b. Setelah dibuat kerucut, jari-jari pada juring lingkaran akan menjadi garis pelukis kerucut, sehingga nilai \(s = 10 \text{ cm}\)
Selanjutnya kita hitung jari-jari alas kerucut yang terbentuk,
Luas selimut kerucut = \(\pi r s\)
\(\frac{314}{3} = 3,14 \cdot r \cdot 10\)
\(\frac{314}{3} = 31,4 \cdot r\)
\(r = \frac{314}{3\times 31,4}\)
\(r = \frac{10}{3}\text{ cm}\)
Untuk mencari tinggi kerucut gunakan rumus Pythagoras
\(r^2 + t^2 = s^2\)
\((\frac{10}{3})^2 + t^2 = 10^2\)
\(\frac{100}{9} + t^2 = 100\)
\( t^2 = 100 – \frac{100}{9} \)
\( t^2 = \frac{800}{9} \)
\( t = \sqrt{\frac{800}{9}} \)
\( t = \frac{20}{3}\sqrt{2} \text{ cm} \)
c. Volume kerucut = \(\frac{1}{3}\cdot\pi r^2 \cdot t\)
= \(\frac{1}{3}\cdot 3,14 \cdot \frac{10}{3} \cdot \frac{10}{3} \cdot \frac{20}{3}\sqrt{2}\)
= \(\frac{6280}{81}\sqrt{2} \text{ cm}^3\)
Soal 4
Diketahui volume sebuah kerucut adalah 324π cm³ dan luas alas kerucut sebesar 81π cm². Tentukan luas permukaan kerucut tersebut
Volume kerucut = \(\frac{1}{3}\times \text{ luas alas } \times \text{ tinggi}\)
\(324 \pi = \frac{1}{3}\cdot 81 \pi \cdot t\)
\(324 \cancel{\pi} = 27 \cancel{\pi} \cdot t\)
\(t = \frac{324}{27}\)
\(t = 12 \text{ cm}\)
Tinggi kerucut didapat 12 cm, selanjutnya jari-jari dapat dicari dari informasi luas alas kerucut
Luas alas kerucut = \(81 \pi\) cm²
\(\cancel{\pi} r^2 = 81 \cancel{\pi}\)
\(r^2 = 81\)
\(r = \sqrt{81} = 9 \text{ cm}\)
Jari-jari kerucut didapat 9 cm, selanjutnya untuk mencari panjang garis pelukis gunakan rumus Pythagoras
\(r^2 + t^2 = s^2\)
\(9^2 + 12^2 = s^2\)
\(225 = s^2\)
\(s = \sqrt{225} = 15 \text{ cm}\)
Luas permukaan kerucut = \(\pi r(r + s)\)
Luas permukaan kerucut = \(\frac{22}{7} \cdot 9(9 +15)\)
Luas permukaan kerucut = \(\frac{22}{7} \cdot 9(24)\)
Luas permukaan kerucut = \(\frac{4752}{7} = 678,86 \text{ cm}^2\)
Soal 5
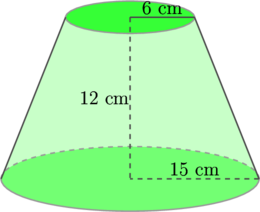
Gambar di atas adalah sebuah kerucut terpancung dengan tinggi 12 cm, jari-jari alas 15 cm, dan jari-jari atap 6 cm. Tentukan volume kerucut terpancung tersebut
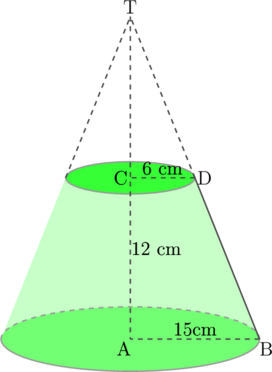
Dengan menggunakan prinsip kesebangunan segitiga, terlihat bahwa ΔTCD sebangun dengan ΔTAB
\(\frac{\text{TC}}{\text{TA}} = \frac{\text{CD}}{\text{AB}}\)
\(\frac{\text{TC}}{\text{TC} + 12} = \frac{6}{15}\:\:\:\:\:\color{blue}\text{kalikan silang}\)
\(15\cdot \text{TC} = 6\cdot (\text{TC} + 12)\)
\(15\cdot \text{TC} = 6\cdot \text{TC} + 72\)
\(15\cdot \text{TC} – 6\cdot \text{TC} = 72\)
\(9\cdot \text{TC} = 72\)
\(\text{TC} = \frac{72}{9} = 8 \text{ cm}\)
Volume kerucut terpancung = volume kerucut yang besar – volume kerucut yang kecil
Kerucut yang besar memiliki jari-jari = AB dan tinggi = TA
Kerucut yang kecil memiliki jari-jari = CD dan tinggi = TC
Volume kerucut terpancung = \(\frac{1}{3}\pi \cdot \text{AB}^2 \cdot \text{TA} – \frac{1}{3}\pi \cdot \text{CD}^2 \cdot \text{TC}\)
Volume kerucut terpancung = \(\frac{1}{3}\frac{22}{7} \cdot 15^2 \cdot 20 – \frac{1}{3}\frac{22}{7} \cdot 6^2 \cdot 8\)
Volume kerucut terpancung = \(\frac{99000}{21} – \frac{6336}{21}\)
Volume kerucut terpancung = \(\frac{92664}{21} = 4412,57 \text{ cm}^3\)
