SOAL
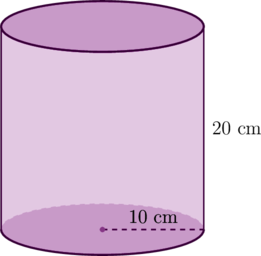
Volume tabung di bawah ini adalah… cm³
Pembahasan:
\(\text{Volume tabung} = \pi r^2 t\)
\(3.14 \cdot 10^2 \cdot 20\)
\(314 \cdot 20\)
\(6280 \text{ cm}^3\)
SOAL
Perhatikan gambar berikut:

Sebuah karton berbentuk persegi panjang dengan ukuran panjang 44 cm dan lebar 15 cm. Karton tersebut akan digulung membentuk tabung. Volume maksimum tabung yang terbentuk adalah… cm³
Pembahasan:
Saat karton digulung menjadi sebuah tabung, maka panjang karton akan menjadi keliling alas tabung, dan lebar karton akan menjadi tinggi tabung.
\(\text{Keliling alas tabung} = 44 \text{ cm}\)
\(2\pi r = 44\)
\(2\cdot \frac{22}{7} \cdot r = 44\)
\(\frac{\cancelto{1}{44}}{7}\cdot r = \cancelto{1}{44}\)
\(r = 7 \text{ cm}\)
\(\text{Volume tabung} = \pi r^2 t\)
\(\text{Volume tabung} = \frac{22}{7}\cdot 7^2 \cdot 15\)
\(\text{Volume tabung} = \frac{22}{\cancel{7}}\cdot \cancel{7} \cdot 7 \cdot 15\)
\(\text{Volume tabung} = 2310 \text{ cm}^3\)
SOAL
Sebuah gelas berbentuk tabung memiliki tinggi 24 cm. Gelas tersebut kemudiaan diisi dengan air sampai penuh sebanyak 480 ml. Luas alas gelas tersebut adalah… cm²
Pembahasan:
Volume gelas sama dengan volume air yang diisikan sampai penuh, yaitu sebesar 480 ml atau setara dengan 480 cm³.
\(\text{Volume tabung} = \text{luas alas} \times \text{ tinggi}\)
\(480 \text{ cm}^3 = \text{luas alas} \times \text{24 cm}\)
\(\text{luas alas} = 480 \div 24\)
\(\text{luas alas} = 20 \text{ cm}^2 \)
SOAL
Sebuah tabung tanpa tutup memiliki diameter alas 28 cm dan tinggi 40 cm. Luas permukaan tabung tersebut adalah… cm²
Pembahasan:
Luas permukaan tabung tanpa tutup = luas alas + luas selimut tabung
\(\pi r^2 + 2\pi r t\)
\(\frac{22}{7} \cdot 14^2 + 2\cdot \frac{22}{7} \cdot 14 \cdot 40\)
\(\frac{22}{\cancelto{1}{7}} \cdot \cancelto{2}{14} \cdot 14 + 2\cdot \frac{22}{\cancelto{1}{7}} \cdot \cancelto {2}{14} \cdot 40\)
\(616 + 3520\)
\(4136 \text{ cm}^2\)
SOAL
Sebuah tabung memiliki diameter alas 42 cm dan luas selimut 1320 cm². Volume tabung tersebut adalah… liter
Pembahasan:
Jari-jari tabung sama dengan setengah diameter alas = ½ × 42 cm = 21 cm
Langkah 1 : mencari tinggi tabung
\(\text{Luas selimut tabung} = 2\pi r t\)
\(1320 = 2\cdot \frac{22}{\cancelto{1}{7}}\cdot \cancelto {3}{21} \cdot t\)
\(1320 = 132\cdot t\)
\(t = 1320 \div 132 = 10 \text{ cm}\)
Langkah 2 : menghitung volume tabung
\(\text{Volume tabung} = \pi r^2 t\)
\(\text{Volume tabung} = \frac{22}{\cancelto{1}{7}}\cdot \cancelto {3}{21} \cdot 21 \cdot 10\)
\(\text{Volume tabung} = 13.860 \text{ cm}^3\)
\(\text{Volume tabung} = 13.860 \text{ ml}\)
\(\color{blue}\text{ 1 cm}^3 = 1 \text{ ml}\)
\(\text{Volume tabung} = 13,86 \text{ liter}\)
\(\color{blue}\text{ 1 liter = 1000 ml}\)
SOAL
Sebuah wadah berbentuk tabung dengan luas alas 64 cm² dan tinggi 15 cm. Seperempat bagian wadah tersebut telah terisi air. Volume air yang harus ditambahkan ke dalam wadah agar wadah terisi penuh dengan air adalah… ml
Pembahasan:
Karena wadah ¼ bagiannya sudah terisi oleh air, maka volume air yang ditambahkan adalah 1 − ¼ bagian atau ¾ bagian lagi agar wadah terisi penuh dengan air.
\(\text{Volume air yang ditambahkan} = \frac{3}{4}\times \text{ volume wadah}\)
\(\text{Volume air yang ditambahkan} = \frac{3}{4}\times \text{ luas alas} \times \text{ tinggi}\)
\(\text{Volume air yang ditambahkan} = \frac{3}{\cancelto {1}{4}}\times \cancelto{16}{64} \times 15\)
\(\text{Volume air yang ditambahkan} = 720 \text{ cm}^3\)
\(\text{Volume air yang ditambahkan} = 720 \text{ ml}\)
SOAL
Perhatikan gambar berikut:
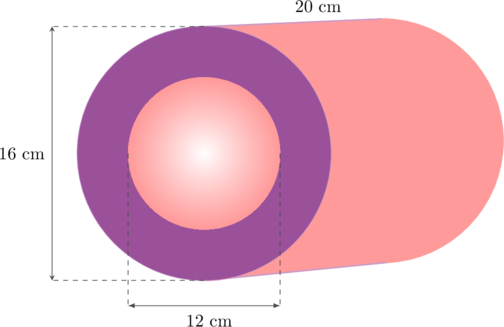
Sebuah potongan pipa besi memiliki panjang 20 cm, diameter bagian luar 16 cm, dan diameter bagian dalamnya 12 cm. Volume pipa besi tersebut adalah… cm³
Pembahasan:
Volume pipa besi = volume tabung bagian luar − volume tabung bagian dalam
Jari-jari tabung bagian luar (R) = ½ × 16 cm = 8 cm
Jari-jari tabung bagian dalam (r) = ½ × 12 cm = 6 cm
\(\text{Volume pipa besi} = \pi \text{R}^2 \text{t} – \pi \text{r}^2 \text{t}\)
\(\pi \text{t} (\text{R}^2 – \text{r}^2)\)
\(\frac{22}{7}\cdot 20 (8^2 – 6^2)\)
\(\frac{22}{7}\cdot 20 (64 – 36)\)
\(\frac{22}{\cancelto{1}{7}}\cdot 20 \cdot \cancelto {4}{28} \)
\(1760 \text{ cm}^3\)
SOAL
Perhatikan gambar berikut:
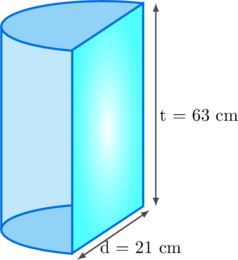
Sebuah potongan kayu berbentuk setengah tabung memiliki diameter 21 cm dan tinggi 63 cm. Luas permukaan potongan kayu tersebut adalah… cm²
Pembahasan:
Luas permukaan potongan kayu = \(\frac{1}{2} \times\) luas permukaan tabung + luas penampang yang berbentuk persegi panjang
Jari-jari potongan kayu = \(\frac{1}{2} \times 21 = \frac{21}{2} \text{ cm}\)
\(\text{Luas permukaan kayu} = \frac{1}{2}\times 2\pi r (r + t) + (21 \times 63)\)
\(\text{Luas permukaan kayu} = \frac{1}{2}\times 2\cdot\frac{22}{7} \cdot \frac{21}{2}(\frac{21}{2} + 63) + 1323\)
\(\text{Luas permukaan kayu} = \frac{1}{\cancel{2}}\times \cancel{2}\cdot\frac{22}{\cancelto{1}{7}} \cdot \frac{22}{7}\cdot \frac{\cancelto{21}{147}}{2} + 1323\)
\(\text{Luas permukaan kayu} = 22 \cdot \frac{22}{\cancelto{1}{7}}\cdot \frac{\cancelto{3}{21}}{2} + 1323\)
\(\text{Luas permukaan kayu} = 22 \cdot \cancelto{11}{22}\cdot \frac{3}{\cancelto{1}{2}} + 1323\)
\(\text{Luas permukaan kayu} = 22 \cdot 11\cdot 3 + 1323\)
\(\text{Luas permukaan kayu} = 726+ 1323\)
\(\text{Luas permukaan kayu} = 2049\text{ cm}^2\)
SOAL
Sebuah gelas berbentuk tabung diisi dengan air setengah bagian. Gelas tersebut memiliki ukuran diameter 10 cm dan tinggi 18 cm. Jika ke dalam gelas tersebut dimasukkan 2 buah kelereng identik yang memiliki volume masing-masing 196,25 cm³, maka ketinggian air di dalam gelas akan menjadi… cm. (Gunakan \(\pi = 3,14\))
Pembahasan:
Langkah 1 : Menentukan tinggi air mula-mula
\(\text{Tinggi air mula-mula} = \frac{1}{2}\times \text{ tinggi gelas}\)
\(\text{Tinggi air mula-mula} = \frac{1}{2}\times \text{18 cm}\)
\(\text{Tinggi air mula-mula} = \text{9 cm}\)
Langkah 2 : Menghitung volume 2 buah kelereng
Volume 2 buah kelereng
\(\text{V} = 2 \times 196,25 = 392,5 \text{ cm}^3\)
Langkah 3 : Menghitung kenaikan tinggi air setelah kelereng dimasukan
Misalkan tinggi air setelah kelereng dimasukkan adalah \(h\)
Volume kenaikan air = volume 2 kelereng yang dimasukkan
\(\pi r^2 h = 392,5 \)
\(3,14\cdot 5^2 \cdot h = 392,5 \)
\(78,5\cdot h = 392,5 \)
\(h = 392,5 \div 78,5\)
\(h = 3925 \div 785\)
\(h = 5 \text{ cm}\)
Tinggi air di dalam gelas sekarang dihitung dengan menjumlahkan tinggi air mula-mula dengan kenaikan tinggi air setelah kelereng dimasukkan ke dalam gelas
Jadi tinggi air di dalam gelas sekarang menjadi 9 cm + 5 cm = 14 cm
SOAL
Adi ingin membuat sebuah tabung yang berjari-jari 14 cm dan tinggi 22 cm dari kertas karton. Jika kertas karton luasnya 3500 cm², maka sisa karton yang tidak terpakai untuk membuat tabung adalah… cm²
Pembahasan:
Langkah 1: Menghitung luas permukaan tabung
\(\text{Luas permukaan tabung} = 2\pi r(r + t)\)
\(\text{Luas permukaan tabung} = 2\cdot \frac{22}{\cancelto{1}{7}}\cdot\cancelto{2}{14}(14 + 22)\)
\(\text{Luas permukaan tabung} = 88\times 36 = 3168 \text{ cm}^2\)
Langkah 2: Menghitung sisa karton yang tidak dipakai
\(\text{Sisa karton } = \text{luas karton} – \text{luas permukaan tabung}\)
\(\text{Sisa karton } = 3500 – 3168\)
\(\text{Sisa karton } = 332 \text{ cm}^2\)
