Soal 01
Dari tabel di bawah ini, manakah pernyataan yang benar mengenai tabung?
| Pernyataan | Jumlah sisi | Jumlah rusuk | Jumlah titik sudut |
| (1) | 2 | 0 | 1 |
| (2) | 2 | 1 | 1 |
| (3) | 3 | 2 | 0 |
| (4) | 3 | 1 | 0 |
(A) (1)
(B) (2)
(C) (3)
(D) (4)
Jawaban: C
Tabung memiliki sisi sebanyak 3 (terdiri dari alas, tutup, dan selimut), rusuk sebanyak 2, dan tidak memiliki titik sudut.
Soal 02
Total luas permukaan sebuah silinder yang berjari-jari 3,5 cm dan tinggi 11,5 cm adalah…
(A) 330 cm²
(B) 333 cm²
(C) 334 cm²
(D) 335 cm²
Total luas permukaan silinder = 2πr(r + h)
Total luas permukaan silinder = \(2 \cdot \dfrac{22}{7} \cdot \dfrac{7}{2} \left(\dfrac{7}{2} + \dfrac{23}{2}\right)\)
Total luas permukaan silinder = \(\cancel{2} \cdot \dfrac{22}{\cancel{7}} \cdot \dfrac{\cancel{7}}{\cancel{2}} \cdot \dfrac{30}{2}\)
Total luas permukaan silinder = \(22 \cdot 15\)
Total luas permukaan silinder = \(330 \text{ cm}^2\)
Soal 03
Luas selimut sebuah tabung adalah 1650 cm². Jika tinggi tabung adalah 25 cm, jari-jari alas tabung adalah…
(A) 21 cm
(B) 14 cm
(C) 10,5 cm
(D) 9 cm
Luas selimut tabung = keliling lingkaran × tinggi tabung
Luas selimut tabung = 2πr × h
\(\cancelto{66}{1650} = 2 \cdot \dfrac{22}{7} \cdot r \cdot \cancelto{1}{25}\)
\(\cancelto{3}{66} = 2 \cdot \dfrac{\cancel{22}}{7} \cdot r\)
\(r = \dfrac{21}{2}\)
\(r = 10,5 \text{ cm}\)
Soal 04
Luas selimut suatu tabung adalah 1540 cm². Jika jari-jari alas tabung 7 cm, volume tabung adalah…
(A) 3950 cm²
(B) 5390 cm²
(C) 6340 cm²
(D) 6540 cm²
Jawaban: B
Luas selimut tabung = 2πr. h
\(1540 = 2 \cdot \dfrac{22}{\cancel{7}} \cdot \cancel{7} \cdot h\)
\(1540 = 44h\)
\(h = \dfrac{1540}{44}\)
\(h = 35 \text{ cm}\)
Volume tabung = πr². h
\(\text{V} = \dfrac{22}{7} \cdot 7^2 \cdot 35\)
\(\text{V} = \dfrac{22}{\cancel{7}} \cdot \cancel{7} \cdot 7 \cdot 35\)
\(\text{V} = 5390 \text{ cm}^3\)
Soal 05
Tiga bola besi identik berjari-jari 6 cm dimasukkan ke dalam wadah berbentuk tabung yang telah terisi air sebagian. Jika jari-jari tabung 24 cm, kenaikan air di dalam tabung tersebut sebesar… cm
(A) 0,5
(B) 1,0
(C) 1,5
(D) 2,0
Volume kenaikan air di dalam tabung = volume 3 bola besi yang dimasukkan
Misal kenaikan air di dalam tabung adalah \(\triangle h\)
\(\pi \cdot \text{R}^2 \cdot \triangle h = 3 \times \dfrac{4}{3} \cdot \pi \cdot \text{r}^3 \)
\(\cancel{\pi} \cdot 24^2 \cdot \triangle h = \cancel{3} \times \dfrac{4}{\cancel{3}} \cdot \cancel{\pi} \cdot 6^3 \)
\(\cancel{24} \cdot \cancelto{4}{24} \cdot \triangle h = \cancel{4 \cdot 6} \cdot \cancel{6} \cdot 6\)
\(4 \cdot \triangle h = 6\)
\(\triangle h = \dfrac{6}{4}\)
\(\triangle h = \dfrac{3}{2} \text{ cm} \)
\(\triangle h = 1,5 \text{ cm}\)
Volume sebuah kerucut 12.936 cm³ dan tingginya 28 cm. Luas selimut kerucut tersebut adalah…
(A) 2.130 cm²
(B) 2.230 cm²
(C) 2.240 cm²
(D) 2.310 cm²
Jawaban: D
Volume kerucut = \(\dfrac{1}{3} \cdot \pi r^2 \cdot h\)
\(12.936 = \dfrac{1}{3} \cdot \dfrac{22}{\cancel{7}} \cdot r^2 \cdot \cancelto{4}{28}\)
Kedua ruas dikali 3
\(38.808 = 88 r^2\)
\(r^2 = \dfrac{38.808}{88}\)
\(r^2 = 441\)
\(r = \sqrt{441}\)
\(r = 21 \text{ cm}\)
Selanjutnya menentukan panjang garis pelukis (s) menggunakan rumus Pythagoras.
\(r^2 + h^2 = s^2\)
\(21^2 + 28^2 = s^2\)
\(441 + 784 = s^2\)
\(s^2 = 1225\)
\(s = \sqrt{1225}\)
\(s = 35 \text{ cm}\)
Luas selimut kerucut = π r s
Luas selimut kerucut = \(\dfrac{22}{\cancel{7}} \cdot \cancelto{3}{21} \cdot 35\)
Luas selimut kerucut = \(2.310 \text{ cm}^2\)
Perhatikan gambar tabung, bola, dan kerucut berikut.

Pada gambar di atas tabung, bola, dan kerucut memiliki tinggi dan jari-jari yang sama.
Perbandingan volume tabung, bola, dan kerucut berturut-turut adalah…
(A) 1 : 2 : 3
(B) 3 : 2 : 1
(C) 1 : 4 : 6
(D) 2 : 5 : 9
Jawaban: B
Pada bola
Tinggi bola = \(2r\)
\(h = 2r\)
\(r = \dfrac{1}{2}h\)
| Volume Tabung | Volume Bola | Volume Kerucut |
| \(\cancel{\pi} r^2 h\) | \(\dfrac{4}{3} \cancel{\pi} r^3\) | \(\dfrac{1}{3} \cancel{\pi} r^2 h\) |
| \(\cancel{r^2} h\) | \(\dfrac{4}{3} \cancelto{r}{r^3}\) | \(\dfrac{1}{3} \cancel{r^2} h\) |
| \(h\) | \(\dfrac{4}{3} r\) | \(\dfrac{1}{3} h\) |
| \(\cancelto{1}{h}\) | \(\dfrac{4}{3} \cdot \dfrac{1}{2} \cancel{h}\) | \(\dfrac{1}{3} \cancel{h}\) |
| \(1\) | \(\dfrac{2}{3}\) | \(\dfrac{1}{3}\) |
| \(3\) | \(2\) | \(1\) |
Jadi, perbandingan volume tabung, bola, dan kerucut secara berturut-turut adalah 3 : 2 : 1.
Volume sebuah tabung adalah 400 cm³. Jika tinggi tabung diperbesar menjadi 1,5 kali semula dan jari-jari tabung dikecilkan menjadi 0,5 kali semula, volume tabung sekarang menjadi…
(A) 400 cm³
(B) 350 cm³
(C) 200 cm³
(D) 150 cm³
Jawaban: D
\(\text{h}_2 = \dfrac{3}{2} \text{ h}_1 \rightarrow \dfrac{\text{h}_2}{\text{h}_1} = \dfrac{3}{2}\)
\(\text{r}_2 = \dfrac{1}{2} \text{ r}_1 \rightarrow \dfrac{\text{r}_2}{\text{r}_1} = \dfrac{1}{2}\)
\(\dfrac{\text{V}_2}{\text{V}_1} = \dfrac{\cancel{\pi} \cdot \text{ r}_2^2 \cdot \text{ h}_2}{\cancel{\pi} \cdot \text{ r}_1^2 \cdot \text{ h}_1}\)
\(\dfrac{\text{V}_2}{400} = \left(\dfrac{\text{r}_2}{\text{r}_1} \right)^2 \cdot \dfrac{\text{h}_2}{\text{h}_1}\)
\(\dfrac{\text{V}_2}{400} = \left(\dfrac{1}{2} \right)^2 \cdot \dfrac{3}{2}\)
\(\dfrac{\text{V}_2}{400} = \dfrac{1}{4} \cdot \dfrac{3}{2}\)
\(\text{V}_2 = \dfrac{3}{8} \cdot 400\)
\(\text{V}_2 = 150 \text{ cm}^3\)
Jadi, volume tabung sekarang menjadi 150 cm³
Sebuah bola karet berdiameter 10 cm. Bola tersebut kemudian dipompa sehingga diameternya bertambah 1 cm. Selisih luas permukaan bola setelah dipompa dan sebelum dipompa adalah…
(A) \(15\pi \text{ cm}^2\)
(B) \(18\pi \text{ cm}^2\)
(C) \(20\pi \text{ cm}^2\)
(D) \(21\pi \text{ cm}^2\)
Jawaban: D
\(\text{Luas permukaan bola} = 4 \pi r^2\)
karena \(r = \dfrac{1}{2}d\) maka rumusnya dapat ditulis:
\(\text{Luas permukaan bola} = 4 \pi \left(\dfrac{1}{2}d \right)^2 = \pi d^2\)
\(\text{Luas permukaan awal} = \pi (10)^2 = 100 \pi \text{ cm}^2\)
\(\text{Luas permukaan akhir} = \pi (11)^2 = 121 \pi \text{ cm}^2\)
Selisih luas permukaan akhir dan awal = \(121 \pi \:-\: 100 \pi = \color{blue} 21 \pi \text{ cm}^2\)
Perhatikan gambar berikut.
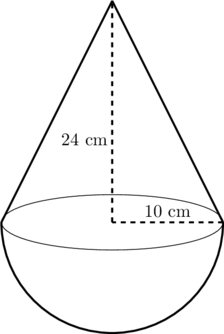
Gambar di atas adalah sebuah liontin yang terdiri dari sebuah kerucut dan setengah bola. Jika jari-jari kerucut sama dengan jari-jari bola sebesar 10 cm dan tinggi kerucut 24 cm, total luas permukaan liontin tersebut sebesar…
(A) 200π cm²
(B) 400π cm²
(C) 450π cm²
(D) 460π cm²
Jawaban: D
Total luas permukaan liontin = luas selimut kerucut + ½ × luas bola
Total luas permukaan liontin = \(\pi\cdot r \cdot s + \dfrac{1}{2} \cdot 4\pi \cdot r^2\)
s = panjang garis pelukis kerucut
\(s^2 = 10^2 + 24^2\)
\(s^2 = 100 + 576\)
\(s^2 = 676\)
\(s = \sqrt{676}\)
\(s = 26 \text{ cm}\)
Total luas permukaan liontin = \(\pi\cdot 10 \cdot 26 + \dfrac{1}{2} \cdot 4\pi \cdot 10^2\)
Total luas permukaan liontin = \(260\pi + 200\pi\)
Total luas permukaan liontin = \(460\pi \)
Perhatikan gambar berikut.
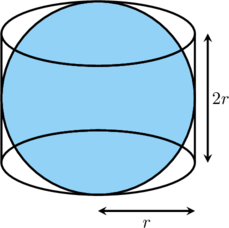
Sebuah bola berada di dalam sebuah tabung. Bola menyinggung semua sisi tabung. Jika jari-jari tabung adalah \(r\) dan tinggi tabung \(2r\), perbandingan luas permukaan tabung dan bola berturut-turut adalah…
(A) \(1 : 1\)
(B) \(1 : 2\)
(C) \(2 : 1\)
(D) \(3 : 2\)
Jawaban: D
Total luas permukaan tabung : luas bola = 2πr(r + h) + 4πr²
h = tinggi tabung = 2r
Total luas permukaan tabung : luas bola = 2πr(r + 2r) : 4πr²
Total luas permukaan tabung : luas bola = 2πr(3r) : 4πr²
Total luas permukaan tabung : luas bola = 6πr² : 4πr²
Total luas permukaan tabung : luas bola = 6 : 4
Total luas permukaan tabung : luas bola = 3 : 2
Jika luas permukaan sebuah bola adalah 900π cm², volume bola tersebut adalah…
(A) 4000π cm²
(B) 45000π cm²
(C) 4800π cm²
(D) 5000π cm²
Jawaban: B
Luas permukaan bola = 4πr²
900π = 4πr²
Bagi kedua ruas dengan π
900 = 4r²
Bagi kedua ruas dengan 4
225 = r²
\(\text{r} = \sqrt{225}\)
\(\text{r} = 15 \text{ cm}\)
Volume bola = \(\dfrac{4}{3} \pi r^3\)
Volume bola = \(\dfrac{4}{3} \pi 15^3\)
Volume bola = \(\dfrac{4}{\cancel{3}} \pi \cancelto{5}{15} \cdot 15 \cdot 15\)
Volume bola = \(4500 \pi\)
