Bagian-bagian Tabung
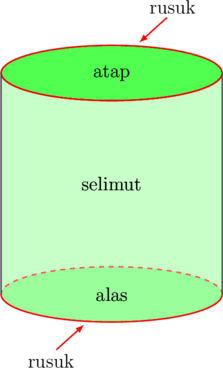
• Jumlah rusuk tabung = 2 buah
• Jumlah sisi tabung = 3 buah, terdiri dari 2 buah sisi datar (alas dan atap) dan 1 buah sisi lengkung (selimut tabung)
• Jumlah titik sudut = 0
Volume dan Luas Permukaan Tabung
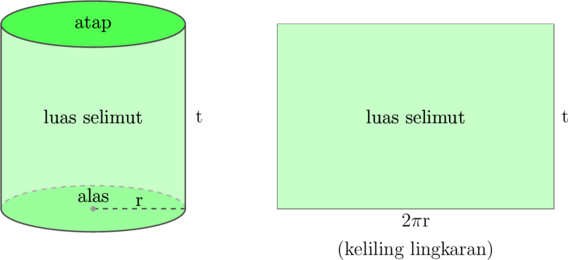
\(\text{Volume tabung = luas alas × tinggi}\)
\(\text{Volume tabung} = \pi r^2 \times t\)
Selimut sebuah tabung jika dibuka akan berbentuk persegi panjang, dengan ukuran panjang merupakan keliling lingkaran alas dan ukuran lebar adalah tinggi tabung. Luas selimut tabung dapat dicari dengan mengalikan keliling lingkaran dengan tinggi tabung.
Luas permukaan tabung merupakan penjumlahan dari luas alas, luas atap, dan luas selimut.
\(\text{LP} = \pi r^2 + \pi r^2 + 2\pi r t\)
\(\text{LP} = 2\pi r(r + t)\)
CONTOH SOAL
Soal 1
Sebuah tabung memiliki jari-jari alas 7 cm dan memiliki tinggi 12 cm. Tentukan:
a. Volume tabung
b. Luas selimut tabung
c. Luas permukaan tabung
a. Volume tabung = \(\pi r^2 t\)
\(\frac{22}{\cancel{7}}\times \cancel{7} \times 7 \times 12\)
1848 cm³
b. Luas selimut tabung = \(2\pi r t \)
\(2\times \frac{22}{7}\times 7 \times 12\)
528 cm²
c. Luas permukaan tabung = \(2\pi r(r + t)\)
\(2\times \frac{22}{\cancel{7}}\times \cancel{7}(7 + 12)\)
836 cm²
Soal 2
Diketahui sebuah tabung tanpa tutup berdiameter 20 cm dan tinggi 25 cm. Tentukan:
a. Volume tabung
b. Luas selimut tabung
c. Luas permukaan tabung
Jari-jari tabung = ½ × diameter tabung
\(r = 10 \text{ cm}\)
a. Volume tabung = \(\pi r^2 t\)
\(3.14 \times 10^2 \times 25\)
7850 cm³
b. Luas selimut tabung = \(2\pi r t \)
\(2\times 3.14\times 10 \times 25\)
1570 cm²
c. Luas permukaan tabung tanpa tutup = luas alas + luas selimut
\(\pi r^2 + 2\pi r t\)
\(3.14 \times 10^2 + 2\times 3.14 \times 10 \times 25\)
1884 cm²
Soal 3
Sebuah tabung memiliki luas selimut 440 cm² dan tinggi 14 cm. Berapakah jari-jari tabung tersebut?
Penyelesaian:
Luas selimut tabung = \(2\pi r t \)
\(440 = 2\cdot \frac{22}{7}\cdot r \cdot 14 \)
\(440 = 88r\)
\(r = \frac{440}{88}\)
\(r = 5 \text{ cm }\)
Soal 4
Sebuah tabung memiliki diameter alas 16 cm. Jika luas selimut tabung tersebut 240 \(\pi\) cm², maka tentukan volume tabung tersebut.
Luas selimut tabung = \(2\pi r t \)
\(240 \cancel{\pi} = 2\cdot \cancel{\pi} \cdot 8 \cdot t\)
\(240 = 16 \cdot t\)
\(t = \frac{240}{16}\)
\(t = 15 \text{ cm}\)
Volume tabung = \(\pi r^2 t\)
Volume tabung = \(\frac{22}{7}\cdot 8^2 \cdot 15\)
Volume tabung = \(\frac{22}{7}\cdot 64 \cdot 15\)
Volume tabung = \(\frac{21120}{7} = 3017,143 \text{ cm}^3\)
Soal 5
Sebuah tabung memiliki total luas permukaan sebesar 266 \(\pi\) cm². Jika tinggi tabung tersebut 12 cm, maka tentukan volume tabung tersebut.
Total luas permukaan tabung = \(2\pi r(r + t)\)
\(266 \cancel{\pi} = 2\cdot \cancel{\pi} \cdot r(r + 12)\)
\(266 = 2r^2 + 24r\)
\(0 = 2r^2 + 24r – 266\:\:\:\:\:\color{blue}\text{bagi kedua ruas dengan 2}\)
\(0 = r^2 + 12r – 133\:\:\:\:\:\color{blue}\text{faktorkan}\)
\(0 = (r + 19)(r – 7)\)
\(r = -19 \text{ (tidak memenuhi)}\)
\(r = 7 \text{ cm} \)
Volume tabung = \(\pi r^2 t\)
Volume tabung = \(\frac{22}{7}\cdot 7^2\cdot 12\)
Volume tabung = 1848 cm³
Soal 6
Sebuah gelas kaca berbentuk tabung memiliki jari-jari alas 7 cm dan tinggi 10 cm. Berapa banyak air diperlukan untuk dapat mengisi setengah bagian gelas kaca tersebut.
Volume air yang diperlukan = ½ × volume tabung
\(\frac{1}{2}\times \pi r^2 t\)
\(\frac{1}{2} \times \frac{22}{\cancel{7}}\times \cancel{7} \times 7 \times 10\)
\(770 \text{ cm}^3\)
\(770 \text{ ml}\)
Soal 7
Sebuah batu dengan volume 4096 \(\pi\) cm³ dimasukkan ke dalam tabung yang berisi air. Jika jari-jari tabung tersebut 32 cm, maka tentukan kenaikan tinggi air di dalam tabung setelah batu dimasukkan.
Penyelesaian:
Misalkan kenaikan air dalam tabung sebesar \(h\) cm
Volume kenaikan air di dalam tabung = volume batu yang dimasukkan
\(\pi r^2 h = 4096 \pi\)
\(\cancel{\pi} 32^2\cdot h = 4096 \cancel{\pi}\)
\(1024\cdot h = 4096 \)
\(h = \frac{4096}{1024}\)
\(h = 4 \text{ cm}\)
Jadi kenaikan tinggi air di dalam tabung sebesar 4 cm
Soal 8
Sebuah pipa besi memiliki panjang 2 meter, diameter luar 42 mm, dan memiliki ketebalan 3,5 mm. Tentukan volume pipa besi tersebut.
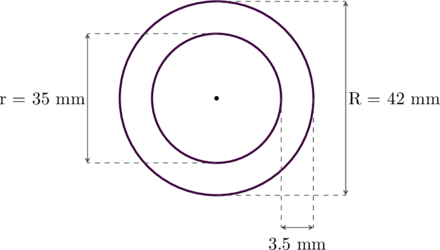
Panjang pipa besi = tinggi tabung = 2 meter = 2000 mm
Volume pipa besi = volume tabung bagian luar − volume tabung bagian dalam
\(\text{Volume pipa besi} = \pi \text{R}^2 \text{t} – \pi \text{r}^2 \text{t}\)
\(\text{Volume pipa besi} = \frac{22}{7} \cdot 42^2 \cdot 2000 – \frac{22}{7} \cdot 35^2 \cdot 2000\)
\(\text{Volume pipa besi} = \frac{22}{\cancelto{1}{7}} \cdot \cancelto{6}{42} \cdot 42\cdot 2000 – \frac{22}{\cancelto{1}{7}} \cdot \cancelto{5}{35} \cdot 35 \cdot 2000\)
\(\text{Volume pipa besi} = 11.088.000 – 7.700.000\)
\(\text{Volume pipa besi} = 3.388.000\text{ mm}^3\)
\(\text{Volume pipa besi} = 3,388\text{ dm}^3 = 3,388 \text{ liter}\)
Soal 9
Sebuah karton berbentuk persegi panjang dengan ukuran panjang 31,4 cm dan lebar 10 cm akan digulung menjadi selimut tabung. Tentukan volume maksimum tabung yang terbentuk.
Saat karton digulung menjadi selimut tabung, panjang karton akan sama dengan keliling alas dan lebar karton akan menjadi tinggi tabung.
Luas selimut tabung = 31,4 cm × 10 cm
Luas selimut tabung = 314 cm²
\(2\pi \text{ r} \text{ t} = 314\)
\(2\cdot 3,14\cdot\text{ r} \cdot 10 = 314\)
\(2\cdot \cancelto{1}{3,14}\cdot\text{ r} \cdot 10 = \cancelto{100}{314}\)
\(20\cdot\text{ r} = 100\)
\(\text{ r} = 100 \div 20 = 5 \text{ cm}\)
\(\text{Volume tabung} = \pi \text{ r}^2\text{ t} \)
\(\text{Volume tabung} = 3,14 \cdot 5^2 \cdot 10\)
\(\text{Volume tabung} = 785 \text{ cm}^3\)
Soal 10
Perhatikan gambar berikut:
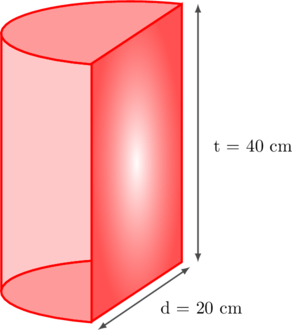
Sebuah benda padat berbentuk setengah tabung, memiliki diameter 20 cm dan tinggi 40 cm. Tentukan luas permukaan benda tersebut.
Luas permukaan benda yang berbentuk setengah tabung dapat kita hitung dengan mencari setengah luas permukaan total tabung ditambah dengan luas irisan yang berbentuk persegi panjang.
Jari-jari alas tabung = ½ × diameter = ½ × 20 = 10 cm
\(\text{Luas permukaan benda} = \frac{1}{2}\cdot 2\pi \text{r (r + t)} + (20 \text{ cm} \times 40 \text { cm})\)
\(\text{Luas permukaan benda} = \frac{1}{\cancel{2}}\cdot \cancel{2}\cdot 3,14 \cdot 10(10 + 40) + 800 \text{ cm}^2\)
\(\text{Luas permukaan benda} = 3,14 \cdot 10(50) + 800 \text{ cm}^2\)
\(\text{Luas permukaan benda} = 1570 + 800 \text{ cm}^2\)
\(\text{Luas permukaan benda} = 2370\text{ cm}^2\)
