\(\text{U}_1 + \text{U}_2 + \text{U}_3 + \dotso \)
\(\text{a} + \text{ar} + \text{ar}^2 + \dotso \)
Jika rasio deret geometri terletak antara \(-1\) dan \(1\) maka deret geometri tersebut akan konvergen (menuju satu titik pertemuan), sehingga deret geometri tak hingga dapat dihitung.
Rumus jumlah deret geometri tak hingga:
\(\color{blue} \text{S}_{\infty} = \dfrac{\text{a}}{1\:-\:\text{r}}\)
Jumlah tak hingga suku-suku ganjil
\(\text{U}_1 + \text{U}_3 + \text{U}_5 + \dotso \)
\(\text{a} + \text{ar}^2 + \text{ar}^4 + \dotso \)
Rasio = \(\dfrac{\text{ar}^2}{\text{a}} = \text{r}^2\)
\(\color{blue} \text{S}_{\infty \text{ ganjil}} = \dfrac{\text{a}}{1\:-\:\text{r}^2}\)
Jumlah tak hingga suku-suku genap
\(\text{U}_2 + \text{U}_4 + \text{U}_6 + \dotso \)
\(\text{ar} + \text{ar}^3 + \text{ar}^5 + \dotso \)
Rasio = \(\dfrac{\text{ar}^3}{\text{ar}} = \text{r}^2\)
\(\color{blue} \text{S}_{\infty \text{ genap}} = \dfrac{\text{ar}}{1\:-\:\text{r}^2}\)
Rumus panjang lintasan bola yang dijatuhkan
Sebuah bola dijatuhkan dari ketinggian \(a\) dan tinggi pantulannya selalu menjadi \(r\) kali ketinggian sebelumnya.
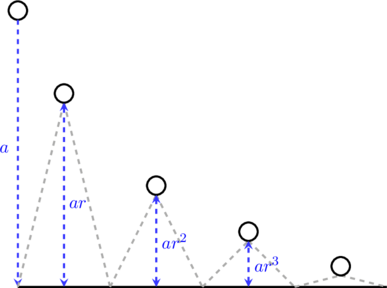
Panjang lintasan bola sejak pertama kali dijatuhkan sampai akhirnya berhenti adalah:
\(\color{blue}\text{L} = \text{a} + \text{2ar} + \text{2ar}^2 + \text{2ar}^3 + \dotso\)
\(\color{blue}\text{L} = \text{2a} + \text{2ar} + \text{2ar}^2 + \text{2ar}^3 + \dotso – \:\text{a}\)
\(\color{blue}\text{L} = 2(\text{a} + \text{ar} + \text{ar}^2 + \text{ar}^3 + \dotso) – \:\text{a}\)
\(\color{blue}\text{L} = 2\left(\dfrac{\text{a}}{1\:-\:\text{r}}\right)\:-\:\text{a}\)
