Teman-teman kita akan membuat sketsa grafik fungsi eksponen \(f(x) = 2^x\)
- Karena \(a>1\) maka grafik fungsi eksponen akan selalu naik
- Titik potong dengan sumbu \(y\) dapat kita cari dengan memasukkan nilai \(x = 0\) sehingga didapat titik (0, 1)
- Asimtot mendatar berada di garis \(y = 0\) atau sumbu \(x\)
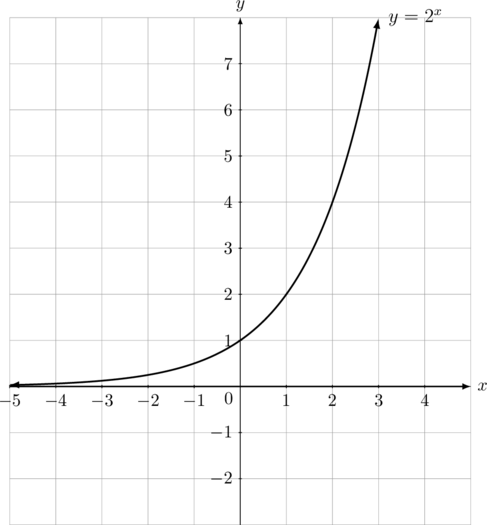
Domain fungsi = \(\lbrace x \arrowvert x \in \Re \rbrace\)
Range fungsi = \(\lbrace y \arrowvert y > 0, y \in \Re \rbrace\)
Selanjutnya, kita akan membuat sketsa grafik fungsi eksponen \(f(x) = (\frac{1}{2})^x\) atau \(f(x) = 2^{-x}\)
- Karena \(a < 1\) maka grafik fungsi eksponen akan selalu turun
- Titik potong dengan sumbu \(y\) dapat kita cari dengan memasukkan nilai \(x = 0\) sehingga didapat titik (0, 1)
- Asimtot mendatar berada di garis \(y = 0\) atau sumbu \(x\)
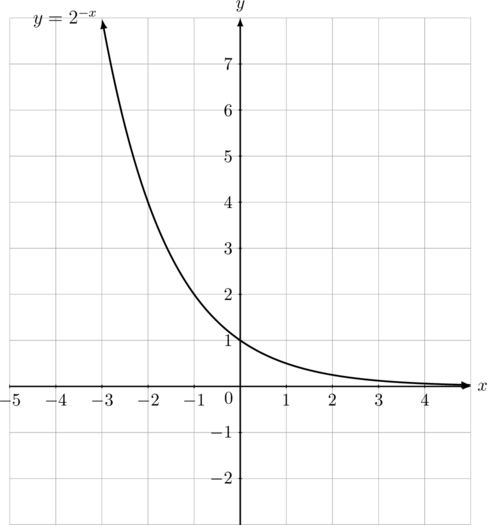
Domain fungsi = \(\lbrace x \arrowvert x \in \Re \rbrace\)
Range fungsi = \(\lbrace y \arrowvert y > 0, y \in \Re \rbrace\)
Pergeseran Fungsi Eksponen \(f(x) = 2^x\)
Geser Naik/Turun
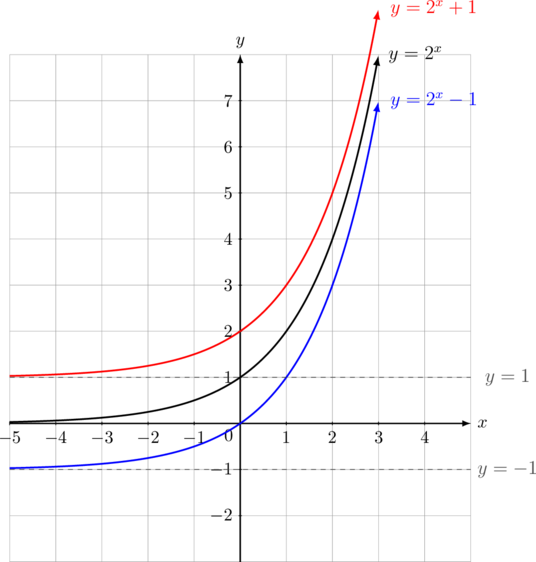
Keterangan:
- Grafik \(y=2^x + 1\) didapat dengan menggeser grafik \(y = 2^x\) sebesar 1 satuan ke atas
- Grafik \(y=2^x – 1\) didapat dengan menggeser grafik \(y = 2^x\) sebesar 1 satuan ke bawah
Geser Kanan/Kiri
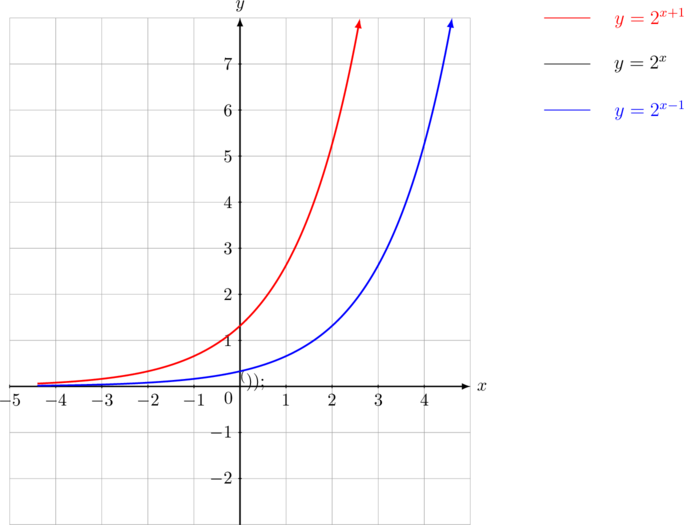
Keterangan:
- Grafik \(y=2^{x + 1}\) didapat dengan menggeser grafik \(y = 2^x\) sebesar 1 satuan ke kiri
- Grafik \(y=2^{x – 1}\) didapat dengan menggeser grafik \(y = 2^x\) sebesar 1 satuan ke kanan
