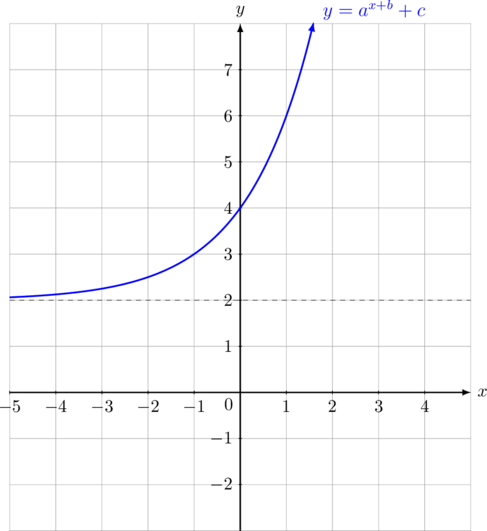
Persamaan grafik fungsi eksponen di bawah ini adalah …
(A) \(y = 2^{x + 1} + 1\)
(B) \(y = 2^{x + 1} + 2\)
(C) \(y = 2^{x + 2} + 1\)
(D) \(y = 2^{x + 2} + 3\)
(E) \(y = 2^{x + 3} + 1\)
Jawaban: B
Dari grafik fungsi eksponen diketahui bahwa asimtot mendatar berada di garis \(y = 2\), sehingga nilai \(c = 2\)
Titik potong sumbu \(y\) berada di \((0, 4)\)
\(y = a^{x + b} + c\)
\(4 = a^{0 + b} + 2\)
\(4 = a^b + 2\)
\(\text{Sehingga, } a^b = 2\dotso\dotso \color{red}(1)\)
Grafik juga melewati titik \((1, 6)\),
\(y = a^{x + b} + c\)
\(6 = a^{1 + b} + 2\)
\(6 = a^1\cdot a^b + 2\:\:\:\:\:\:\color{blue}\text{substitusikan persamaan 1}\)
\(6 = a \cdot 2 + 2\)
\(2a = 4\)
\(a = 2\)
\(a^b = 2\)
\(2^b = 2^1\rightarrow b = 1\)
Jadi persamaan fungsi eksponennya adalah: \(y = 2^{x + 1} + 2\)
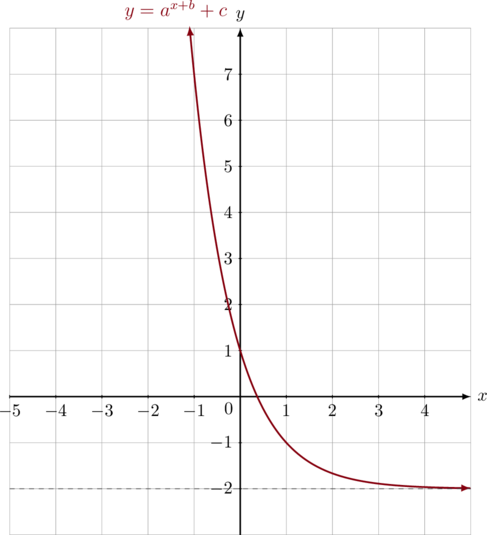
Persamaan grafik fungsi eksponen di bawah ini adalah …
(A) \(y = 2^{x + 1} \:-\: 1\)
(B) \(y = 2^{x + 2} + 2\)
(C) \(y = \left(\dfrac{1}{3}\right)^{x \:-\: 1} \:-\: 2\)
(D) \(y = \left(\dfrac{1}{3}\right)^{x \:-\: 1} + 2\)
(E) \(y = \left(\dfrac{1}{3}\right)^{x +2} \:-\: 3\)
Jawaban: C
Dari grafik fungsi eksponen diketahui bahwa asimtot mendatar berada di garis \(y = -2\), sehingga nilai \(c = -2\)
Titik potong sumbu \(y\) berada di \((0, 1)\)
\(y = a^{x + b} + c\)
\(1 = a^{0 + b} \:-\: 2\)
\(1 = a^b \:-\:2\)
\(\text{Sehingga, } a^b = 3\dotso\dotso \color{red}(1)\)
Grafik juga melewati titik \((-1, 7)\),
\(y = a^{x + b} + c\)
\(7 = a^{-1 + b} \:-\: 2\)
\(7 = a^{-1}\cdot a^b \:-\: 2\:\:\:\:\:\:\color{blue}\text{substitusikan persamaan 1}\)
\(7 = \dfrac{1}{a} \cdot 3 \:-\: 2\)
\(7 + 2 = \dfrac{3}{a}\)
\(9 = \dfrac{3}{a}\)
\(9a = 3\)
\(a = \dfrac{3}{9} = \dfrac{1}{3}\)
\(a^b = 3\)
\(\left(\dfrac{1}{3}\right)^b = 3\rightarrow b = -1\)
Jadi persamaan fungsi eksponennya adalah: \(y = \left(\dfrac{1}{3}\right)^{x \:-\: 1} \:-\:2\)
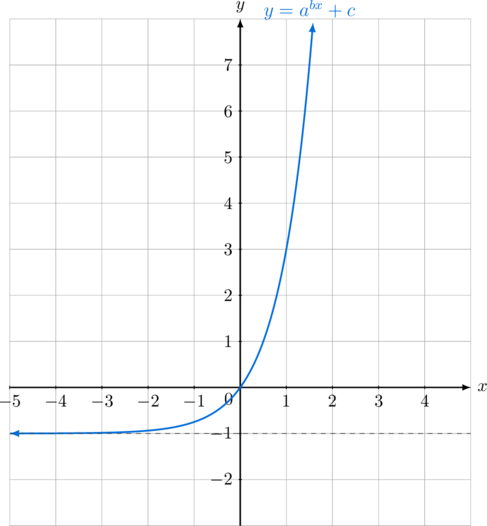
Persamaan grafik fungsi eksponen di bawah ini adalah …
(A) \(y = 2^{x}\:-\: 1\)
(B) \(y = 2^{2x} \:-\: 1\)
(C) \(y = 2^{2x} \:-\: 2\)
(D) \(y = 2^{3x} \:-\: 1\)
(E) \(y = 2^{3x} + 1\)
Jawaban: B
Dari grafik fungsi eksponen diketahui bahwa asimtot mendatar berada di garis \(y = -1\) sehingga nilai \(c = -1\)
Grafik melalui titik \((1, 3)\),
\(y = a^{bx} + c\)
\(3 = a^b \:-\: 1\)
\(a^b = 3 + 1 = 4\dotso\dotso\color{red} (1)\)
Grafik juga melalui titik \((\frac{1}{2}, 1)\),
\(1 = a^{\frac{1}{2}b} \:-\: 1\)
\(1 = a^{\frac{1}{2}}\cdot a^b\:-\: 1\:\:\:\:\:\color{blue}\text{substitusikan persamaan 1}\)
\(1 = a^{\frac{1}{2}}\cdot 4\:-\: 1\)
\(2 = 4a^{\frac{1}{2}}\)
\(\frac{1}{2} = a^{\frac{1}{2}}\:\:\:\:\:\color{blue}\text{kuadratkan kedua ruas}\)
\(\frac{1}{4} = a\)
\(a^b = 4\)
\((\frac{1}{4})^b = 4\)
\((2^{-2})^b = 4\)
\(2^{-2b} = 2^2\)
\(-2b = 2\)
\(b = -1\)
Jadi persamaan grafik fungsi eksponennya adalah:
\(y=(\frac{1}{4})^{-x} \:-\: 1\)
\(y=(2^{-2})^{-x} \:-\: 1\)
\(\color{purple} y=2^{2x} \:-\:1\)
Grafik fungsi \(f(x) = -2^{a – bx}\) memotong sumbu \(y\) di titik \((0, -8)\). Jika grafik \(f(x)\) digeser ke atas 2 satuan akan menghasilkan grafik fungsi \(g(x)\) yang melewati titik \((1, -14)\). Persamaan grafik fungsi \(g(x)\) adalah ….
(A) \(g(x) = -2^{3 + x} + 2\)
(B) \(g(x) = -2^{3 + x} \:-\: 2\)
(C) \(g(x) = -\left(\dfrac{1}{4}\right)^{x \:-\:3} + 2\)
(D) \(g(x) = -\left(\dfrac{1}{2}\right)^{x \:-\:3} + 2\)
(E) \(g(x) = -\left(\dfrac{1}{2}\right)^{x \:-\:2} + 1\)
Jawaban: A
\(f(x) = -2^{a \:-\: bx}\) memotong sumbu \(y\) di titik \((0, -8)\)
\(-8 = -2^a\)
\(8 = 2^a\)
\(a = 3\)
\(f(x) = -2^{3\:-\: bx}\) kemudian digeser ke atas 2 satuan menjadi fungsi \(g(x)\)
\(g(x) = f(x) + 2\)
\(g(x) = -2^{3 \:-\: bx} + 2\)
\(g(x)\) melewati titik \((1, -14)\)
\(-14 = -2^{3\:-\:b} + 2\)
\(-16 = -2^{3\:-\:b}\)
\(2^4 = 2^{3 \:-\:b}\)
\(3 \:-\: b = 4\)
\(-b = 4 \:-\: 3\)
\(-b = 1\)
\(b = -1\)
Jadi fungsi \(g(x)\) adalah:
\(g(x) = -2^{3 + x} + 2\)
Grafik fungsi \(f(x) = 8\left(\dfrac{1}{2}\right)^x\) digeser ke kiri 1 satuan, lalu digeser ke bawah 2 satuan akan menghasilkan fungsi \(g(x)\). Nilai \(g(2)\) adalah
(A) \(-2\)
(B) \(-1\)
(C) 0
(D) 1
(E) 2
Jawaban: B
\(f(x) = 8\left(\dfrac{1}{2}\right)^x\) digeser ke kiri 1 satuan, lalu digeser ke bawah 2 satuan, akan menghasilkan fungsi \(g(x) = 8\left(\dfrac{1}{2}\right)^{x \color{blue}+ 1\color{black}} \color{red} – \:2\)
\(g(2) = 8\left(\dfrac{1}{2}\right)^{2 + 1} – \:2\)
\(g(2) = 8\left(\dfrac{1}{2}\right)^3 – \:2\)
\(g(2) = \cancel{8}\left(\dfrac{1}{\cancel{8}}\right) – \:2\)
\(g(2) = 1\: – \:2 = -\:1\)
Persamaan \(y = 5(2^{2x}\:-\:1)\) dapat diubah menjadi …
(A) \(y = 2^{x + ^2\log_{}{5}}\:-\:5\)
(B) \(y = 2^{x + ^4\log_{}{5}}\:-\:5\)
(C) \(y = 4^{x + ^4\log_{}{5}}\:-\:6\)
(D) \(y = 4^{x + ^4\log_{}{5}}\:-\:5\)
(E) \(y = 4^{x \:-\: ^4\log_{}{5}}\:-\:5\)
Jawaban: D
\(y = 5(4^{2x}\:-\:1)\)
\(y = 5(4^x\:-\:1)\)
\(y = 5\cdot 4^x\:-\:5\)
\(y = 4^{^4\log_{}{5}}\cdot 4^x\:-\:5\:\:\:\:\:\color{blue}\text{ingat: } a^{^a\log_{}{b}} = b\)
\(y = 4^{^4\log_{}{5} + x}\:-\:5\)
\(y = 4^{x + ^4\log_{}{5}}\:-\:5\)
Jika \(\text{f(x)} = 5^x\), maka \(\text{f(a + b + 2c)} = \dotso\)
(A) \(\text{f(a)} \cdot \text{f(b)} \cdot \text{2f(c)}\)
(B) \(\text{f(a)} \cdot \text{f(b)} \cdot \text{f(c)}\)
(C) \(\text{f(a)} \cdot \text{f(b)} \cdot [\text{f(c)}]^2\)
(D) \(\text{f(a)} \cdot \text{2f(b)} \cdot [\text{f(c)}]^2\)
(E) \(\text{f(a)} \cdot \text{f(b)} \cdot [\text{f(c)}]^4\)
Jawaban: C
\(\text{f(a + b + 2c)} = 5^{a + b + 2c}\)
\(\text{f(a + b + 2c)} = 5^a \cdot 5^b \cdot 5^{2c}\)
\(\text{f(x)} = 5^x \rightarrow \color{blue} \text{f(a)} = 5^a\)
\(\text{f(x)} = 5^x \rightarrow \color{blue} \text{f(b)} = 5^b\)
\(\text{f(x)} = 5^x \rightarrow \color{blue} \text{f(c)} = 5^c\)
\(\text{f(a + b + 2c)} = 5^a \cdot 5^b \cdot [5^{c}]^2\)
\(\text{f(a + b + 2c)} = \text{f(a)} \cdot \text{f(b)} \cdot [\text{f(c)}]^2\)
Persamaan fungsi eksponen yang melalui titik (0, 2), (1, 4), dan (2, 10) adalah …
(A) \(\text{f(x)} = 3^x \:-\: 1\)
(B) \(\text{f(x)} = 3^x + 1\)
(C) \(\text{f(x)} = 3^x + 2\)
(D) \(\text{f(x)} = 3^x + 3\)
(E) \(\text{f(x)} = 3^{-x} + 1\)
Jawaban: B
Misal persamaan fungsi eksponennya adalah \(\text{f(x)} = a^{x + b} + c\)
Substitusikan titik-titik yang diketahui ke dalam persamaan \(\text{f(x)} = a^{x + b} + c\)
\((0, 2) \rightarrow 2 = a^{0 + b} + c\dotso\dotso (1)\)
\((1, 4) \rightarrow 4 = a^{1 + b} + c\dotso\dotso (2)\)
\((2, 10) \rightarrow 10 = a^{2 + b} + c\dotso\dotso (3)\)
Eliminasi \(c\) persamaan (1) dan (2), dengan cara kurangkan persamaan (1) dengan persamaan (2) sehingga didapat:
\(-2 = a^{b}\:-\:a^{1 + b}\)
\(-2 = a^{b}\:-\:a^1\cdot a^b\:\:\:\:\:\color{blue}\text{faktorkan}\)
\(-2 = a^b(1\:-\:a)\dotso\dotso (4)\)
Eliminasi \(c\) persamaan (2) dan (3), dengan cara kurangkan persamaan (2) dengan persamaan (3) sehingga didapat:
\(-6 = a^{1 + b}\:-\:a^{2 + b}\)
\(-6 = a^1\cdot a^b\:-\:a^2\cdot a^b\:\:\:\:\:\color{blue}\text{faktorkan}\)
\(-6 = a^b(a\:-\:a^2)\)
\(-6 = a^b\cdot a(1\:-\:a)\dotso\dotso (5)\)
Bagi persamaan (4) dengan persamaan (5),
\(\dfrac{-2}{-6} = \dfrac{\cancel{a^b}\cancel{(1\:-\:a)}}{\cancel{a^b}\cdot a\cancel{(1\:-\:a)}}\)
\(\dfrac{1}{3} = \dfrac{1}{a}\)
\(a = 3\)
Substitusikan \(a = 3\) ke persamaan (4)
\(-2 = 3^b(1\:-\:3)\)
\(-2 = 3^b (-2)\)
\(1 = 3^b\)
\(b = 0\)
Substitusikan \(b = 0\) ke persamaan (1)
\(2 = a^{b} + c\)
\(2 = 3^{0} + c\)
\(2 = 1 + c\)
\(c = 1\)
Jadi, persamaan grafik fungsi kuadratnya adalah \(\text{f(x)} = 3^x + 1\)
