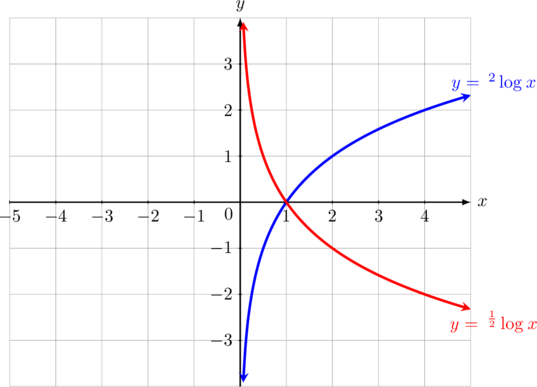
Kurva logaritma dengan basis lebih dari 1
Contoh:
\(y =\:^2\log_{}{x}\)
- Merupakan fungsi naik
- Memotong sumbu \(x\) di titik (1, 0)
- Memiliki asimtot tegak garis \(x = 0\)
Kurva logaritma dengan basis antara 0 dan 1
Contoh:
\(y =\:^{\frac{1}{2}}\log_{}{x}\)
- Merupakan fungsi turun
- Memotong sumbu \(x\) di titik (1, 0)
- Memiliki asimtot tegak garis \(x = 0\)
Pergeseran kurva logaritma \(y = \:^2\log_{}{x}\) ke arah kanan dan ke arah kiri
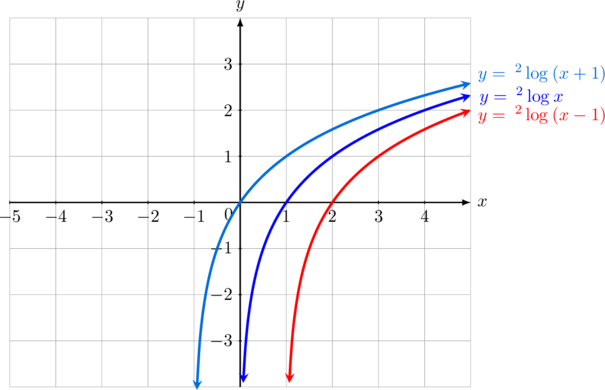
Kurva \(y = \:^2\log_{}{x}\) jika digeser 1 satuan ke kanan akan menjadi kurva \(y = \:^2\log_{}{(x\:-\:1)}\)
Kurva \(y = \:^2\log_{}{x}\) jika digeser 1 satuan ke kiri akan menjadi kurva \(y = \:^2\log_{}{(x + 1)}\)
Pergeseran kurva logaritma \(y = \:^2\log_{}{x}\) ke arah atas dan ke arah bawah
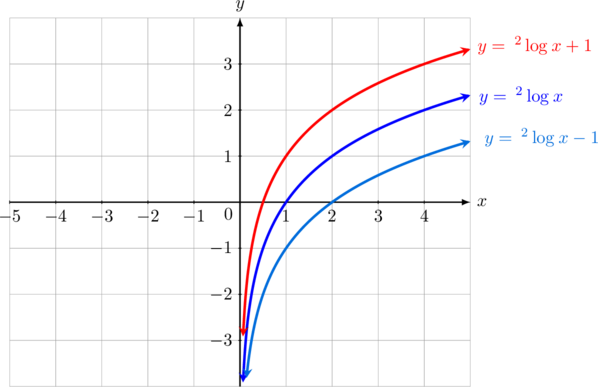
Kurva \(y = \:^2\log_{}{x}\) jika digeser 1 satuan ke atas akan menjadi kurva \(y = \:^2\log_{}{x} + 1\)
Kurva \(y = \:^2\log_{}{x}\) jika digeser 1 satuan ke bawah akan menjadi kurva \(y = \:^2\log_{}{x}\:-\: 1\)
Cara menentukan asimtot tegak
Kurva logaritma memiliki satu buah asimtot tegak. Asimtot tegak ini berupa garis vertikal yang tidak akan pernah dipotong maupun disinggung oleh kurva logaritma.
Untuk persamaan umum \(y = \: ^a\log_{}{(x + b)} + c\), asimtot tegak didapat dari \(x + b = 0\) atau ditulis \(x = – b\)
Contoh:
Tentukan asimtot tegak kurva \(y = \:^3\log_{}{(2x + 4)} \:-\:1\)
Jawab:
Asimtot tegak didapat dari \(2x + 4 = 0\)
\(2x = -4\)
\(x = \frac{-4}{2}\)
\(x = -2\)
Jadi asimtot tegaknya adalah garis \(x = -2\)
