Menentukan domain dan range dari fungsi linear
Bentuk umum fungsi linear \(f(x) = ax + b\)
Domain fungsi linear adalah semua bilangan real
Domain = \(\lbrace x| \: x \in \text{ R}\rbrace\) atau ditulis \((-\infty, \infty)\)
Range fungsi linear adalah semua bilangan real
Range = \(\lbrace y| \: y \in \text{ R}\rbrace\) atau ditulis \((-\infty, \infty)\)
Gambar grafik fungsi linear \(f(x) = 4x + 1\)
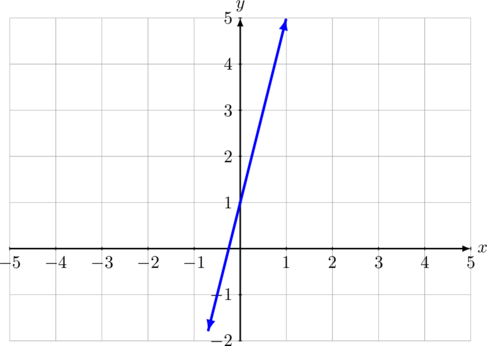
Domain dan range dari \(f(x) = 4x + 1\)
Domain = \(\lbrace x| \: x \in \text{ R}\rbrace\) atau ditulis \((-\infty, \infty)\)
Range = \(\lbrace y| \: y \in \text{ R}\rbrace\) atau ditulis \((-\infty, \infty)\)
Menentukan domain dari suatu fungsi kuadrat
Bentuk umum fungsi kuadrat adalah \(f(x) = ax^2 + bx + c\)
Domain fungsi kuadrat adalah semua bilangan real
Domain = \(\lbrace x| \: x \in \text{ R}\rbrace\) atau ditulis \((-\infty, \infty)\)
Range dari fungsi kuadrat tergantung pada nilai minimum atau nilai maksimum fungsi kuadrat tersebut.
Untuk \(a > 0\) bentuk kurva fungsi kuadrat adalah parabola yang membuka ke atas sehingga memiliki nilai minimum
Range = \(\lbrace y|\: y \geq y_{\text{min}}, \:y \in \text{ R}\rbrace\) atau ditulis \([y_{\text{min}}, \infty)\)
Untuk \(a < 0\) bentuk kurva fungsi kuadrat adalah parabola yang membuka ke bawah sehingga memiliki nilai maksimum
Range = \(\lbrace y | \:y \leq y_{\text{max}}, \:y \in \text{ R}\rbrace\) atau ditulis \((-\infty, y_{\text{max}}]\)
Gambar grafik fungsi kuadrat \(f(x) = 2x^2 + 1\)
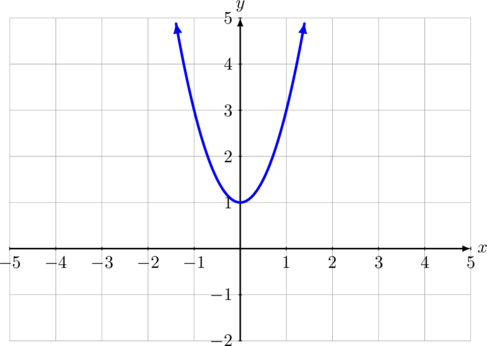
Domain dan range \(f(x) = 2x^2 + 1\)
Domain = \(\lbrace x| \: x \in \text{ R}\rbrace\) atau ditulis \((-\infty, \infty)\)
Range = \(\lbrace y|\: y \geq 1, \:y \in \text{ R}\rbrace\) atau ditulis \([1, \infty)\)
Gambar grafik fungsi kuadrat \(g(x)=-2x^2 + 1\)
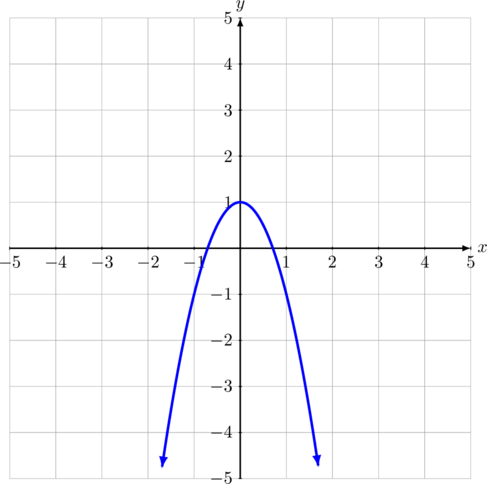
Domain dan range \(f(x) = -2x^2 + 1\)
Domain = \(\lbrace x| \: x \in \text{ R}\rbrace\) atau ditulis \((-\infty, \infty)\)
Range = \(\lbrace y|\: y \leq 1, \:y \in \text{ R}\rbrace\) atau ditulis \((-\infty, 1]\)
Menentukan domain dan range dari fungsi akar pangkat dua
Bentuk umum: \(f(x) = \sqrt{g(x)}\)
Syarat terdefinisi \(g(x) \geq 0\)
Domain dari fungsi akar pangkat dua merupakan himpunan penyelesaian dari \(g(x) \geq 0\)
Range dari fungsi akar pangkat bergantung pada nilai minimum dan maksimum dari batas-batas domain yang telah ditentukan sebelumnya.
Gambar grafik fungsi kuadrat \(f(x) = \sqrt{x\:-\:3}\)
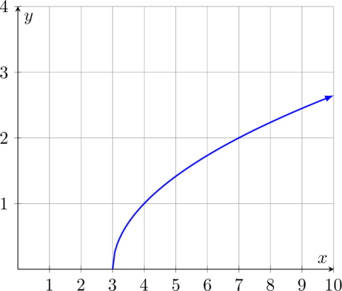
Syarat terdefinisi
\(x\:-\:3 \geq 0\)
\(x \geq 3\)
Domain = \(\lbrace x| \: x \geq 3, \: x \in \text{ R}\) atau ditulis \([3, \infty)\).
Range = \(\lbrace y| \: y \geq 0, \: y\in \text{ R}\) atau ditulis \([0, \infty)\).
Menentukan domain dan range dari suatu fungsi pecahan
Bentuk umum fungsi pecahan \(f(x) = \dfrac{ax + b}{cx + d}\)
Syarat terdefinisi:
\(cx + d \neq 0\) (bagian penyebut tidak boleh sama dengan nol).
\(x\neq -\dfrac{d}{c}\)
Domain dari fungsi pecahan adalah semua \(x\) bilangan real dengan \(x\neq -\dfrac{d}{c}\).
Untuk menentukan range dari fungsi pecahan kita tulis dahulu \(y = \dfrac{ax + b}{cx + d}\)
Kali silang,
\(cxy + dy = ax + b\)
\(cxy\:-\:ax = b\:-\:dy\)
\(x(cy\:-\:a) = b\:-\:dy\)
\(x = \dfrac{b\:-\:dy}{cy\:-\:a}\)
Syarat terdefinisi \(cy\:-\:a \neq 0\)
\(y \neq \dfrac{a}{c}\)
Jadi, range dari fungsi pecahan adalah semua \(y\) bilangan real dengan \(y \neq \dfrac{a}{c}\).
Gambar grafik fungsi pecahan \(f(x) = \dfrac{4x + 1}{2x + 6}\)
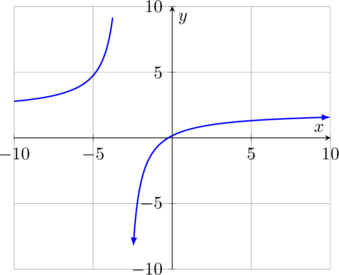
Syarat terdefinisi:
\(2x + 6 \neq 0\)
\(2x \neq -6\)
\(x \neq -\dfrac{6}{2}\)
\(x \neq -3\)
Domain dari \(f(x) = \dfrac{4x + 1}{2x + 6}\) adalah semua \(x\) bilangan real dengan \(x\neq -3\).
Range dari \(f(x) = \dfrac{4x + 1}{2x + 6}\) adalah semua \(y\) bilangan real dengan \(y\neq \dfrac{4}{2} \text{ atau } y \neq 2\).
CATATAN
- Garis \(x = -3\) merupakan asimtot vertikal dari \(f(x) = \dfrac{4x + 1}{2x + 6}\).
- Garis \(y = 2\) merupakan asimtot horizontal dari \(f(x) = \dfrac{4x + 1}{2x + 6}\).
Kurva \(f(x) = \dfrac{4x + 1}{2x + 6}\) tidak pernah memotong maupun menyinggung kedua asimtot tersebut.
