Fungsi adalah suatu relasi yang menghubungkan satu anggota dari suatu himpunan tepat ke satu anggota di himpunan yang lain.
Contoh suatu relasi yang merupakan fungsi
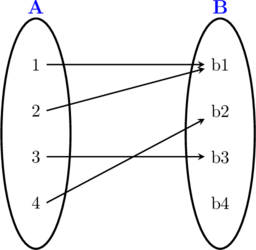
Setiap anggota A dipasangkan tepat ke satu anggota B, sehingga relasi dari A ke B adalah fungsi.
A = {1, 2, 3, 4} disebut dengan domain (daerah asal)
B = {b1, b2, b3, b4} disebut dengan kodomain (daerah kawan)
{b1, b2, b3} disebut dengan range {daerah hasil}
Contoh suatu relasi yang bukan fungsi
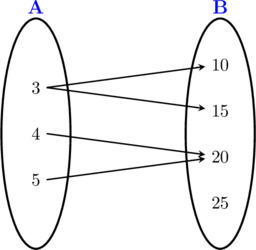
Relasi dari A ke B pada gambar di atas bukan merupakan fungsi karena salah satu anggota dari A yaitu 3 dipasangkan dua kali ke anggota dari B yaitu 10 dan 15.
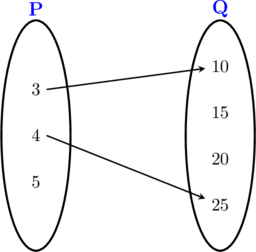
Relasi dari P ke Q pada gambar di atas bukan merupakan fungsi karena ada anggota P yaitu 5 yang tidak dipasangkan dengan anggota Q.
Tes Garis Vertikal
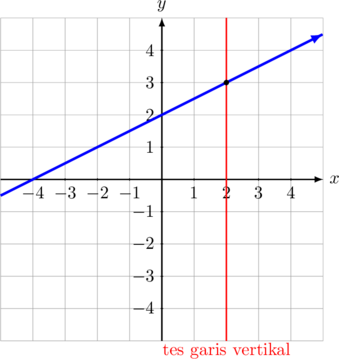
Tes garis vertikal digunakan untuk mengetahui suatu relasi yang digambarkan dalam bentuk grafik merupakan fungsi atau bukan.
Jika garis vertikal digeser ke kiri maupun ke kanan melalui grafik relasi hanya memotong grafik di satu titik saja, maka grafik relasi tersebut merupakan fungsi.
Contoh grafik relasi yang merupakan fungsi
A. Fungsi Linear
\(\color{blue} y = 0,5x + 2\)
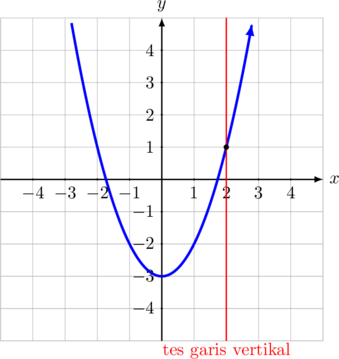
B. Fungsi Kuadrat
\(\color{blue} y = x^2\:-\:3\)
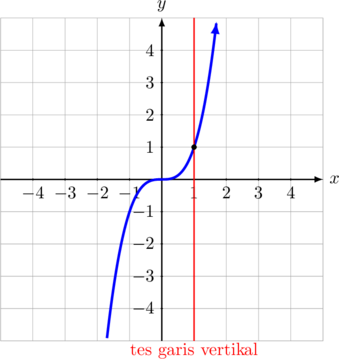
C. Fungsi Pangkat Tiga
\(\color{blue} y = x^3\)
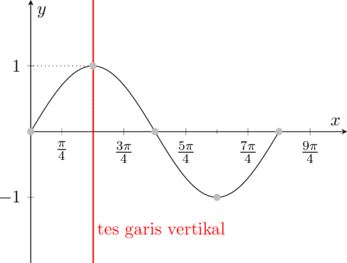
D. Fungsi Sinus
\(\color{blue} y = \sin x\)
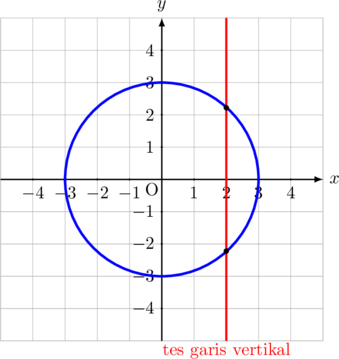
Contoh grafik relasi yang bukan fungsi
A. Persamaan Lingkaran
\(\color{blue} x^2 + y^2 = 9\)
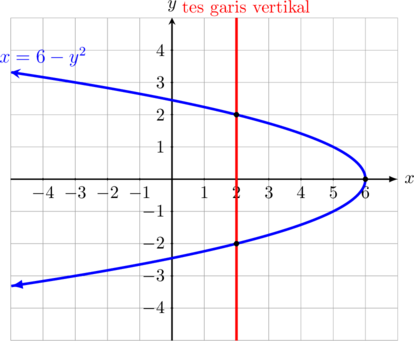
B. Parabola yang membuka ke kiri
\(\color{blue} x = 6 \:-\: y^2\)
Latihan Soal
Soal 01
Jika \(f(2x\:-\:1) = 4x + 5\), \(f(x) = \dotso\)
(A) \(f(x) = 2x + 3\)
(B) \(f(x) = 3x + 2\)
(C) \(f(x) = 7x + 1\)
(D) \(f(x) = x + 10\)
(E) \(f(x) = 2x + 7\)
Soal 02
Jika \(f(6x + a) = 5x + 6\) dan \(f(3) = 8\), maka \(f(2) = \dotso\)
(A) \(\dfrac{42}{5}\)
(B) \(\dfrac{43}{6}\)
(C) \(\dfrac{47}{6}\)
(D) \(\dfrac{48}{6}\)
(E) \(\dfrac{49}{8}\)
Soal 03
Fungsi \(f\) dinyatakan dengan rumus \(f(x) = mx + k\). Jika \(f(2) = 13\) dan \(f(5) = 22\), nilai \(m + k = \dotso\)
(A) 6
(B) 8
(C) 9
(D) 10
(E) 12