Terdapat dua garis sejajar yaitu garis \(g\) dan garis \(h\) yang dipotong oleh sebuah garis transversal \(k\)
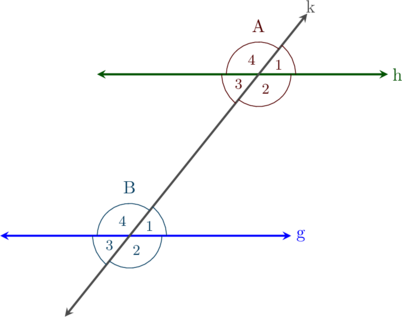
Sudut Sehadap
Berdasarkan gambar di atas, pasangan sudut-sudut yang sehadap adalah:
- \(\angle A_1 \text{ dan } \angle B_1\)
- \(\angle A_2 \text{ dan } \angle B_2\)
- \(\angle A_3 \text{ dan } \angle B_3\)
- \(\angle A_4 \text{ dan } \angle B_4\)
Pasangan sudut yang sehadap memiliki besar yang sama
Sudut Dalam Berseberangan
Berdasarkan gambar di atas, pasangan sudut dalam berseberangan adalah:
- \(\angle A_2 \text{ dan } \angle B_4\)
- \(\angle A_3 \text{ dan } \angle B_1\)
Pasangan sudut dalam berseberangan memiliki besar yang sama
Sudut Luar Berseberangan
Berdasarkan gambar di atas, pasangan sudut luar berseberangan adalah:
- \(\angle A_1 \text{ dan } \angle B_3\)
- \(\angle A_4 \text{ dan } \angle B_2\)
Pasangan sudut luar berseberangan memiliki besar yang sama
Sudut Dalam Sepihak
Berdasarkan gambar di atas, pasangan sudut dalam sepihak adalah:
- \(\angle A_2 \text{ dan } \angle B_1\)
- \(\angle A_3 \text{ dan } \angle B_4\)
Pasangan sudut dalam sepihak jika dijumlahkan hasilnya 180°
\(\angle A_2 \text + \angle B_1 = 180^\circ\)
\(\angle A_3 \text + \angle B_4 = 180^\circ\)
Sudut Luar Sepihak
Berdasarkan gambar di atas, pasangan sudut luar sepihak adalah:
- \(\angle A_1 \text{ dan } \angle B_2\)
- \(\angle A_4 \text{ dan } \angle B_3\)
Pasangan sudut dalam sepihak jika dijumlahkan hasilnya 180°
\(\angle A_ 1 \text + \angle B_2= 180^\circ\)
\(\angle A_4 \text + \angle B_3 = 180^\circ\)
