Sebuah kubus ABCD.EFGH memiliki rusuk yang panjangnya 6 cm. Titik P terletak pada perpanjangan rusuk AB, sehingga BP : AP = 1 : 2. Titik T terletak pada perpanjangan rusuk FG, sehingga GT : FT = 1 : 2. Tentukan jarak titik P ke titik T.
Penyelesaian:
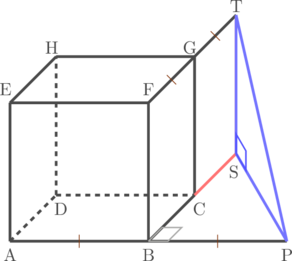
Diketahui:
BP : AP = 1 : 2, maka BP = AB = 6 cm
GT : FT = 1 : 2, maka GT = FG = 6 cm
Perhatikan segitiga siku-siku SBP
\(\text{SB}^2 + \text{BP}^2 = \text{SP}^2\)
\(12^2 + 6^2 = \text{SP}^2\)
\(144+ 36 = \text{SP}^2\)
\(180 = \text{SP}^2\)
\(\text{SP} = \sqrt{180}\)
\(\text{SP} = 6\sqrt{5}\text{ cm}\)
Perhatikan segitiga siku-siku TSP
\(\text{TS}^2 + \text{SP}^2 = \text{PT}^2\)
\(6^2 + (6\sqrt{5})^2 = \text{PT}^2\)
\(36 + 180 = \text{PT}^2\)
\(216 = \text{PT}^2\)
\(\text{PT} = \sqrt{216} =6\sqrt{6}\text{ cm}\)
Jadi jarak titik P ke titik T adalah \(6\sqrt{6}\text{ cm}\)
Kubus ABCD.EFGH memiliki rusuk dengan panjang 6 cm. Tentukan jarak titik B ke garis AG
Penyelesaian:
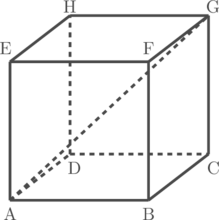
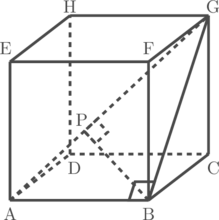
Jarak antara titik B ke garis AG adalah ruas garis yang ditarik dari B tegak lurus dengan garis AG. Ruas garis tersebut adalah BP.
Perhatikan segitiga siku-siku ABG, dengan menggunakan kesamaan mencari luas segitiga ABG kita dapat menghitung panjang BP.
BG adalah diagonal bidang sehingga \(\text{BG} = r\sqrt{2} = 6\sqrt{2}\text{ cm}\)
AG adalah diagonal ruang sehingga \(\text{AG} = r\sqrt{3} = 6\sqrt{3}\text{ cm}\)
\(\frac{1}{2}\cdot \text{ AB } \cdot \text{ BG } = \frac{1}{2}\cdot \text{ AG } \cdot \text{ BP }\)
\(\cancel{\frac{1}{2}}\cdot 6 \cdot 6\sqrt{2} = \cancel{\frac{1}{2}}\cdot 6\sqrt{3} \cdot \text{ BP }\)
\(36\sqrt{2} = 6\sqrt{3} \cdot \text{ BP }\)
\(\text{BP} = \frac{36\sqrt{2}}{6\sqrt{3}}\)
\(\text{BP} = \frac{6\sqrt{2}}{\sqrt{3}}\times \frac{\sqrt{3}}{\sqrt{3}}\)
\(\text{BP} = \frac{6\sqrt{6}}{3}\)
\(\text{BP} = 2\sqrt{6}\text{ cm}\)
Jadi jarak titik B ke garis AG adalah \(2\sqrt{6}\text{ cm}\)
Sebuah kubus ABCD.EFGH memiliki rusuk yang panjangnya 6 cm. Tentukan jarak antara titik H dengan bidang ACF.
Penyelesaian:
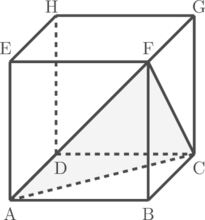
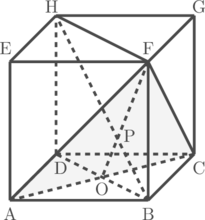
Perhatikan bidang BDHF, dan perhatikan keistimewaan bidang diagonal kubus tersebut:
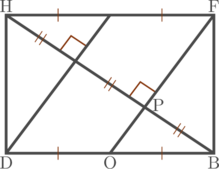
Panjang HP dapat kita hitung dengan perbandingan ruas pada diagonal HB
\(\text{HP} = \frac{2}{3}\times \text{ HB}\)
\(\text{HP}= \frac{2}{3}\times r\sqrt{3}\)
\(\text{HP}= \frac{2}{3}\times 6\sqrt{3}\)
\(\text{HP}= 4\sqrt{3}\text{ cm}\)
Jadi jarak antara titik H dengan bidang ACF = HP = \(4\sqrt{3}\text{ cm}\)
Sebuah kubus ABCD.EFGH memiliki rusuk yang panjangnya 24 cm. Titik P terletak pada perpanjangan rusuk DC, sehingga CP : DP = 1 : 3. Tentukan jarak titik P ke bidang BDHF.
Penyelesaian:
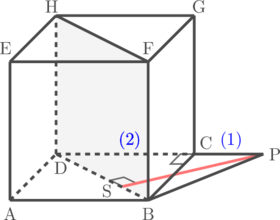
Karena titik P berada pada perpanjangan rusuk DC, dan perbandingan CP : DP = 1 : 3 maka CP = ½ × DC = 12 cm.
Panjang DP = 24 cm + 12 cm = 36 cm
Langkah 1: Proyeksikan titik P pada bidang BDHF
Hasil proyeksi titik P pada bidang BDHF adalah titik S, sehingga jarak titik P ke bidang BDHF adalah PS
Langkah 2: Mencari panjang PS
Kita dapat menghitung panjang PS dengan menggunakan kesamaan mencari luas segitiga DBP
\(\frac{1}{2}\times \text{ BD} \times \text{ PS} = \frac{1}{2}\times \text{ DP} \times \text{ BC}\)
\(\cancel{\frac{1}{2}}\times \cancel{24}\sqrt{2} \times \text{ PS} = \cancel{\frac{1}{2}}\times 36 \times \cancel{24}\)
\(\sqrt{2}\text{ PS} = 36\)
\(\text{ PS} = \frac{36}{\sqrt{2}}\times \frac{\sqrt{2}}{\sqrt{2}}\)
\(\text{ PS} = 18\sqrt{2}\text{ cm}\)
Jadi jarak titik P ke bidang BDHF = PS = \(18\sqrt{2}\text{ cm}\)
Diketahui bidang empat beraturan T.ABC dengan panjang rusuk 8 cm. Tentukan jarak T ke bidang ABC.
Penyelesaian:
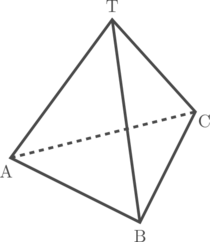
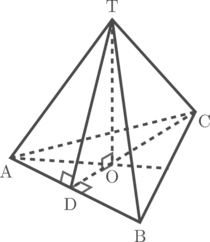
Langkah 1: Proyeksikan titik T ke bidang ABC
Hasil proyeksi T ke bidang ABC adalah titik O, sehingga jarak titik T ke bidang ABC adalah TO
Untuk mencari TO, perhatikan segitiga TDC
Langkah 2: Mencari TD
Lihat segitiga siku-siku TDA
\(\text{AD}^2 + \text{TD}^2 = \text{TA}^2\)
\(4^2 + \text{TD}^2 = 8^2\)
\(16 + \text{TD}^2 = 64\)
\(\text{TD}^2 = 64 – 16\)
\(\text{TD}^2 = 48\)
\(\text{TD} = \sqrt{48} = 4\sqrt{3}\text{ cm}\)
Langkah 3: Mencari OD
Perhatikan alas segitiga ABC
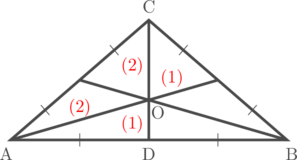
Titik O merupakan perpotongan garis-garis berat pada segitiga ABC
Garis-garis berat tersebut saling membagi dengan perbandingan panjang 1 : 2
Note: garis berat adalah garis yang ditarik dari salah satu titik sudut segitiga sehingga memotong sama panjang sisi dihadapan titik sudut tersebut
\(\text{OD} : \text{OC} = 1 : 2\)
\(\text{OD} = \frac{1}{1+2}\times \text{CD}\)
\(\text{OD} = \frac{1}{3}\times 4\sqrt{3}\:\:\:\:\:\color{blue} \text{CD = TD}\)
\(\text{OD} = \frac{4}{3}\sqrt{3}\text{ cm}\)
Langkah 4: Mencari TO
Perhatikan segitiga siku-siku TOD
\(\text{OD}^2 + \text{TO}^2 = \text{TD}^2\)
\((\frac{4}{3}\sqrt{3})^2 + \text{TO}^2 = (4\sqrt{3})^2\)
\(\frac{16}{3} + \text{TO}^2 = 48\)
\(\text{TO}^2 = 48 – \frac{16}{3}\)
\(\text{TO}^2 = \frac{128}{3}\)
\(\text{TO} = \sqrt{\frac{128}{3}}\)
\(\text{TO} = \frac{8\sqrt{6}}{3}\text{ cm}\)
Jadi jarak titik T ke bidang ABC adalah \(\frac{8\sqrt{6}}{3}\text{ cm}\)
Kubus ABCD.EFGH memiliki panjang rusuk 6 cm. Tentukan jarak antara garis AG dengan garis BD.
Penyelesaian:
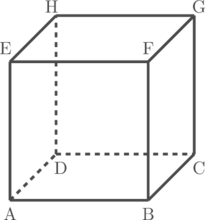
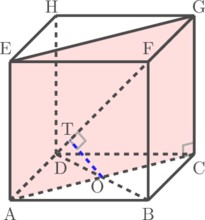
Langkah 1: Menentukan bidang yang memuat AG dan tegak lurus BD
Bidang yang memuat AG dan tegak lurus BD adalah bidang ACGE
Langkah 2: Menentukan titik tembus BD pada bidang ACGE
Titik tembus BD pada bidang ACGE adalah titik O
Jarak antara AG ke BD adalah jarak titik O ke garis AG yaitu OT
Note: Jarak antara garis AG dan BD adalah OT karena OT tegak lurus terhadap garis AG sekaligus tegak lurus terhadap BD
Langkah 3: Mencari panjang OT
Perhatikan segitiga siku-siku ACG
Panjang OT dapat kita cari dengan menggunakan kesamaan mencari luas segitiga ACG
\(\frac{1}{2}\times \text{AC}\times \text{CG} = \frac{1}{2}\times \text{AG}\times \text{OT}\)
\(\cancel{\frac{1}{2}}\times 6\sqrt{2}\times 6 = \cancel{\frac{1}{2}}\times 6\sqrt{3}\times \text{OT}\)
\(\cancelto{6}{36}\sqrt{2} = \cancelto{1}{6}\sqrt{3}\times \text{OT}\)
\(6\sqrt{2} = \sqrt{3}\times \text{OT}\)
\(\text{OT} = \frac{6\sqrt{2}}{\sqrt{3}}\times \color{red} \frac{\sqrt{3}}{\sqrt{3}}\)
\(\text{OT} = 2\sqrt{6}\text{ cm}\)
Jadi jarak antara garis AG dan garis BD adalah \(2\sqrt{6}\text{ cm}\)
Kubus ABCD.EFGH memiliki rusuk yang panjangnya 6 cm. Tentukan jarak antara garis FH ke bidang BDG.
Penyelesaian:
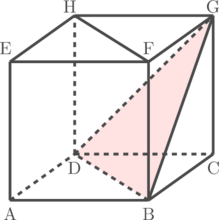
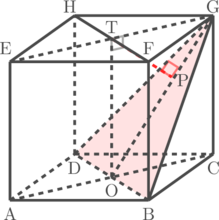
Langkah 1: Tentukan bidang yang tegak lurus dengan bidang BDG
Bidang yang tegak lurus dengan bidang BDG adalah ACGE
Langkah 2: Tentukan garis potong antara bidang ACGE dengan bidang BDG
Garis potong (garis persekutuan) antara bidang ACGE dengan bidang BDG adalah garis OG
Langkah 3: Tentukan titik tembus HF pada bidang ACGE
Titik tembus HF pada ACGE berada di titik T
Langkah 4: Tentukan jarak antara titik T dengan garis OG
Jarak antara titik T ke garis OG adalah TP
Langkah 5: Menghitung panjang TP
Perhatikan segitiga siku-siku OTG
Panjang TP dapat dihitung dengan menggunakan kesamaan mencari luas segitiga OTG
\(\frac{1}{2}\times \text{OT} \times \text{TG} = \frac{1}{2}\times \text{OG} \times \text{TP}\)
\(\text{Note: }\)
\(\text{TG} =\frac{1}{2}\cdot \text{EG} = \frac{1}{2}\cdot 6\sqrt{2} = 3\sqrt{2}\)
\(\text{OG} = \sqrt{\text{OC}^2 + \text{CG}^2}\)
\(\text{OG} = \sqrt{(3\sqrt{2})^2 + 6^2} = \sqrt{54}=3\sqrt{6}\)
\(\frac{1}{2}\times \text{OT} \times \text{TG} = \frac{1}{2}\times \text{OG} \times \text{TP}\)
\(\cancel{\frac{1}{2}}\times 6 \times 3\sqrt{2} = \cancel{\frac{1}{2}}\times 3\sqrt{6} \times \text{TP}\)
\(18\sqrt{2} = 3\sqrt{6} \times \text{TP}\)
\(\text{TP} = \dfrac{18\sqrt{2}}{3\sqrt{6}}\)
\(\text{TP} =\dfrac{6\sqrt{2}}{\sqrt{6}}\times\color{red}\dfrac{\sqrt{6}}{\sqrt{6}}\)
\(\text{TP} =\sqrt{12}\)
\(\text{TP} =2\sqrt{3}\text{ cm}\)
Jadi jarak antara garis FH ke bidang BDG adalah \(2\sqrt{3}\text{ cm}\)
Kubus ABCD.EFGH memiliki rusuk yang panjangnya 6 cm. Tentukan jarak antara bidang ACF ke bidang EGD.
Penyelesaian:
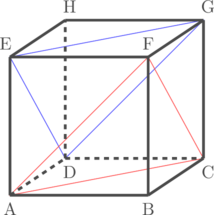
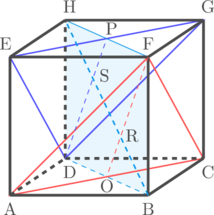
Langkah 1: Buat bidang yang tegak lurus dengan bidang ACF dan EGD
Bidang yang tegak lurus dengan bidang ACF dan EGD adalah bidang BDHF
Langkah 2: Menentukan garis potong antara kedua bidang
Garis potong antara bidang ACF dengan BDHF adalah OF
Garis potong antara bidang DEG dengan BDHF adalah DP
Langkah 3: Menentukan titik tembus HB pada bidang ACF dan EGD
Titik tembus HB pada bidang ACF adalah titik R
Titik tembus HB pada bidang EGD adalah titik S
Langkah 4: Mencari jarak antara titik R dan titik S
Jarak antara bidang ACF dengan bidang EGD sama dengan jarak titik R dan titik S
Perhatikan bidang diagonal kubus BDHF
\(\text{SR} = \frac{1}{3}\times \text{HB}\)
\(\text{SR} = \frac{1}{3}\times 6\sqrt{3} = 2\sqrt{3} \text{ cm}\)
Jadi jarak antara bidang ACF dengan bidang EGD adalah \(2\sqrt{3} \text{ cm}\)
Limas beraturan T.ABCD memiliki panjang rusuk tegak sama dengan rusuk alas. P merupakan titik tengah rusuk AB. Tentukan cosinus sudut antara garis TC dan garis TP.
Penyelesaian:
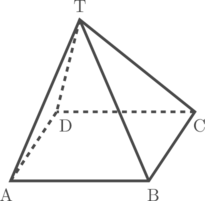
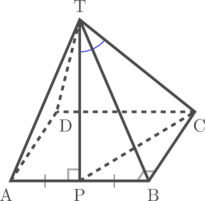
Sudut antara garis TC dan garis TP adalah \(\angle \text{PTC} = \alpha\)
Perhatikan segitiga PTC, terlebih dahulu kita hitung panjang TP dan juga PC
Lihat segitiga siku-siku TPA
Anggap semua rusuk limas beraturan T.ABCD panjangnya 1 satuan
\(\text{AP}^2 + \text{TP}^2 = \text{TA}^2\)
\((\frac{1}{2})^2 + \text{TP}^2 = 1^2\)
\(\frac{1}{4} + \text{TP}^2 = 1\)
\(\text{TP}^2 = 1 – \frac{1}{4}\)
\(\text{TP}^2 = \frac{3}{4}\)
\(\text{TP} = \sqrt{\frac{3}{4}} = \frac{1}{2}\sqrt{3} \text{ satuan}\)
Lihat segitiga siku-siku PBC
\(\text{PB}^2 + \text{BC}^2 = \text{PC}^2\)
\((\frac{1}{2})^2+ 1^2 = \text{PC}^2\)
\(\frac{1}{4} + 1 = \text{PC}^2\)
\(\frac{5}{4} = \text{PC}^2\)
\(\text{PC} = \sqrt{\frac{5}{4}}\)
\(\text{PC} = \frac{1}{2}\sqrt{5}\text{ satuan}\)
Gunakan aturan cosinus pada segitiga PTC
\(\text{PC}^2 = \text{TP}^2 + \text{TC}^2 – 2\cdot \text{TP} \cdot \text{TC}\cdot \cos \alpha\)
\((\frac{1}{2}\sqrt{5})^2 = (\frac{1}{2}\sqrt{3})^2 + 1^2 – \cancel{2}\cdot \frac{1}{\cancel{2}}\sqrt{3} \cdot 1 \cdot \cos \alpha\)
\(\frac{5}{4} = \frac{3}{4} + 1 – \sqrt{3}\cdot \cos \alpha\)
\(\frac{5}{4} – \frac{3}{4} – 1 = – \sqrt{3}\cdot \cos \alpha\)
\(-\frac{1}{2} = – \sqrt{3}\cdot \cos \alpha\)
\(\cos \alpha = \frac{1}{2\sqrt{3}}\times \color{red} \frac{\sqrt{3}}{\sqrt{3}}\)
\(\cos \alpha = \frac{1}{6}\sqrt{3}\)
Jadi cosinus sudut antara garis TC dan garis TP adalah \(\frac{1}{6}\sqrt{3}\)
Penyelesaian:
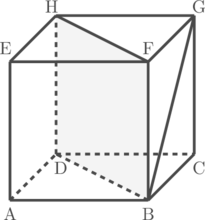
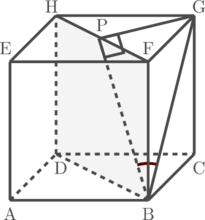
Langkah 1: Proyeksikan garis BG pada bidang BDHF
Proyeksi titik B pada bidang BDHF adalah titik B sendiri
Proyeksi titik G pada bidang BDHF adalah titik P
Sehingga, hasil proyeksi garis BG pada bidang BDHF adalah garis BP
Langkah 2: Tentukan sudut antara garis BG dengan garis BP
Misalkan sudut antara garis BG dengan garis BP adalah \(\alpha\)
Perhatikan segitiga siku-siku BPG
\(\sin \alpha = \frac{\text{PG}}{\text{BG}}\)
\(\sin \alpha = \frac{\frac{1}{2}\cancel{r\sqrt{2}}}{\cancel{r\sqrt{2}}}\)
\(\sin \alpha = \frac{1}{2}\)
\(\alpha = 30^{\circ}\)
Jadi sudut antara garis BG pada bidang BDHF adalah \(30^{\circ}\)
Diketahui limas T.ABC dengan TA tegak lurus bidang ABC. Panjang rusuk AB, AC, BC, dan TA berturut-turut adalah 3 cm, 4 cm, 5 cm, dan \(\frac{9}{5}\) cm. Jika \(\alpha\) sudut antara bidang BCT dengan bidang ABC, maka nilai \(\cos \alpha\) adalah…
A. \(\frac{4}{5}\)
B. \(\frac{3}{5}\)
C. \(\frac{6}{25}\)
D. \(\frac{9}{25}\)
E. \(\frac{12}{25}\)
Jawaban: A
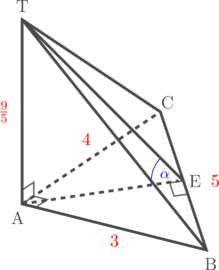
Langkah 1: Tentukan bidang yang tegak lurus dengan bidang BCT dan bidang ABC
Bidang yang tegak lurus dengan BCT dan ABC adalah bidang TAE
Langkah 2: Tentukan garis potong antara bidang TAE dengan bidang BCT dan juga bidang ABC
Garis potong bidang TAE dengan BCT adalah TE
Garis potong bidang TAE dengan ABC adalah AE
Langkah 3: Mencari sudut yang dibentuk antara TE dan AE
Sudut antara bidang BCT dengan bidang ABC sama dengan sudut yang dibentuk oleh garis TE dan garis AE.
Sudut yang dimaksud adalah \(\alpha\)
Perhatikan segitiga siku-siku BAC untuk menghitung panjang AE terlebih dahulu,
Dengan menggunakan kesamaan mencari luas segitiga BAC
\(\frac{1}{2}\times \text{AB} \times \text{AC} = \frac{1}{2}\times \text{BC} \times \text{AE}\)
\(\cancel{\frac{1}{2}}\times 3 \times 4 = \cancel{\frac{1}{2}}\times 5 \times \text{AE}\)
\(12 = 5 \times \text{AE}\)
\(\text{AE} = \frac{12}{5}\)
Perhatikan segitiga siku-siku TAE,
\(\tan \alpha = \dfrac{\text{TA}}{\text{AE}}\)
\(\tan \alpha = \dfrac{\frac{9}{5}}{\frac{12}{5}}\)
\(\tan \alpha = \dfrac{9}{12} = \dfrac{3}{4}\)
\(\cos \alpha = \dfrac{4}{5}\)
