Berikut ini adalah pembahasan mengenai cara mencari sudut antara bidang dengan bidang di dalam kubus dengan terlebih dahulu membuat irisan bidang melalui tiga buah titik pada kubus.
Diketahui kubus ABCD.EFGH dengan panjang rusuk 4 cm. Titik P berada pada rusuk FG dengan perbandingan FP : PG = 3 : 1. Titik Q berada pada rusuk BF dengan perbandingan BQ : QF = 1 : 3. Titik R berada pada rusuk GH dengan perbandingan GR : RH = 1 : 3. Sudut antara bidang yang melalui P, Q, R dan bidang ABCD adalah α. Tentukan nilai tan α.
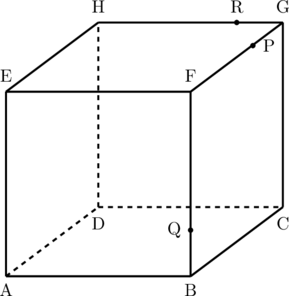
Pembahasan:
Langkah 1: Membuat irisan pada kubus yang melalui titik P, Q, R
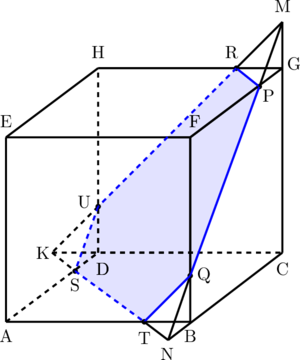
(1) Hubungkan titik P dan R
(2) Hubungkan titik P dan Q
- Perpanjangan PQ ke atas akan memotong rusuk CG di titik M
- Perpanjangan PQ ke bawah akan memotong rusuk CB di titik N
(3) Hubungkan titik M dan R
- Perpanjangan MR ke bawah akan memotong rusuk HG di titik R, HD di titik U, dan rusuk CD di titik K.
(4) Hubungkan titik K dan N
- KN memotong AD di titik S
- KN memotong AB di titik T
(5) Hubungkan titik T dan Q
(6) Hubungkan titik S dan U
(7) Irisan pada kubus yang terbentuk adalah bidang PRUSTQ yang berbentuk segi enam.
Langkah 2: Menentukan bidang yang tegak lurus dengan bidang PRUSTQ dan bidang ABCD
Bidang yang tegak lurus dengan bidang PRUSTQ dan bidang ABCD adalah bidang ACGE
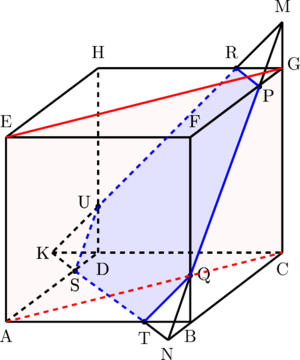
Langkah 3: Menentukan garis potong antara bidang ACGE dengan bidang PRUSTQ dan bidang ABCD
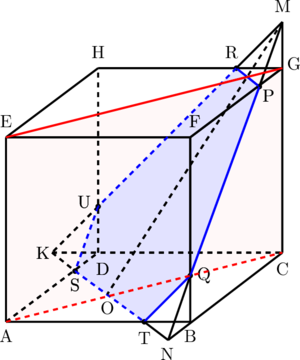
Garis potong antara bidang ACGE dengan bidang PRUSTQ adalah OM
Garis potong antara bidang ACGE dengan bidang ABCD adalah AC
Langkah 4: Menentukan sudut yang dibentuk antara garis OM dan AC
Perhatikan segitiga siku-siku OCM
Sudut yang dibentuk antara garis OM dan AC adalah α
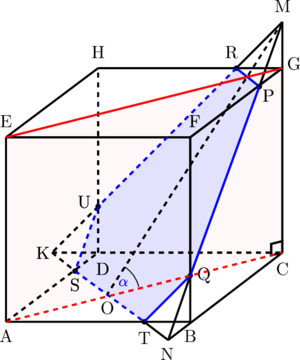
Dengan menggunakan prinsip kesebangunan, ukuran sisi setiap segitiga diperoleh sebagai berikut:
Segitiga siku-siku QBN sebangun dengan segitiga PFQ dan segitiga PGM. Ketiga segitiga tersebut adalah segitiga siku-siku sama kaki.
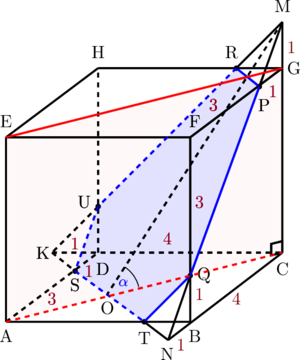
Perhatikan kesebangunan antara segitiga ASO dengan segitiga CNO.

\(\dfrac{\text{AS}}{\text{NC}} = \dfrac{\text{AO}}{\text{OC}}\)
\(\dfrac{3}{5} = \dfrac{4\sqrt{2}\:-\:x}{x}\)
Kali silang,
\(3x = 20\sqrt{2}\:-\:5x\)
\(8x = 20\sqrt{2}\)
\(x = \dfrac{20\sqrt{2}}{8}\)
\(x = \dfrac{5\sqrt{2}}{2}\)
Panjang OC = \(\dfrac{5\sqrt{2}}{2}\)
Pada segitiga siku-siku OCM berlaku:
\(\tan \alpha = \dfrac{\text{CM}}{\text{OC}}\)
\(\tan \alpha = \dfrac{5}{\frac{5\sqrt{2}}{2}}\)
\(\tan \alpha = \dfrac{1}{\frac{\sqrt{2}}{2}}\)
\(\tan \alpha = \dfrac{2}{\sqrt{2}}\)
\(\tan \alpha = \dfrac{2}{\sqrt{2}}\times \color{red} \dfrac{\sqrt{2}}{\sqrt{2}}\)
\(\tan \alpha = \dfrac{2\sqrt{2}}{2}\)
\(\tan \alpha = \sqrt{2}\)
Jadi, nilai \(\tan \alpha = \sqrt{2}\)
