Cara Mengetahui ΔABC dan ΔPQR Sebangun
1. Teorema Sudut-Sudut (A-A)
Dua buah segitiga dikatakan sebangun jika dua sudut yang bersesuaian pada segitiga pertama dan kedua sama besar.

Karena \(\angle \textbf{CAB} = \angle \textbf{RPQ}\) dan \(\angle \textbf{ABC} = \angle \textbf{PQR}\) maka segitiga ABC dan segitiga PQR sebangun.
\(\color{blue} \triangle \textbf{ABC} \sim \triangle \textbf{PQR}\)
2. Teorema Sisi-Sisi-Sisi (S-S-S)
Dua buah segitiga dikatakan sebangun jika sisi-sisi yang bersesuaian memiliki perbandingan yang sama.
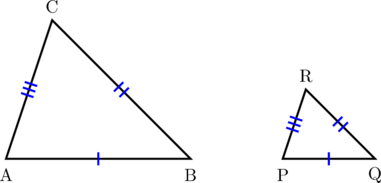
Karena \(\dfrac{\textbf{AB}}{\textbf{PQ}} = \dfrac{\textbf{BC}}{\textbf{QR}} = \dfrac{\textbf{CA}}{\textbf{RP}}\) maka segitiga ABC sebangun dengan segitiga PQR.
\(\color{blue} \triangle \textbf{ABC} \sim \triangle \textbf{PQR}\)
3. Teorema Sisi-Sudut-Sisi (S-A-S)
Dua buah segitiga dikatakan sebangun jika mereka memiliki satu sudut yang sama besar dan panjang sisi-sisi yang mengapit sudut tersebut memiliki perbandingan yang sama.

Karena \(\dfrac{\textbf{BC}}{\textbf{QR}} = \dfrac{\textbf{CA}}{\textbf{RP}}\) dan \(\angle \textbf{BCA} = \angle \textbf{QRP}\) maka segitiga ABC sebangun dengan segitiga PQR.
\(\color{blue} \triangle \textbf{ABC} \sim \triangle \textbf{PQR}\)
Perbandingan sisi pada dua segitiga yang sebangun
Model 01
Diketahui \(\triangle \textbf{ADE} \sim \triangle \textbf{ABC} \)
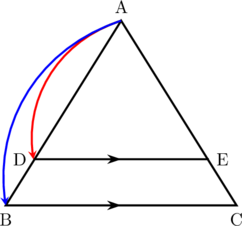
Perbandingan sisi yang berlaku:
$$\bbox[yellow, 5px, border: 2px solid red] {\dfrac{\textbf{AD}}{\textbf{AB}} = \dfrac{\textbf{DE}}{\textbf{BC}} = \dfrac{\textbf{AE}}{\textbf{AC}}}$$
Model 02
Diketahui \(\triangle \textbf{ABC} \sim \triangle \textbf{DEC} \)
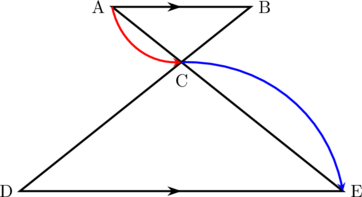
Perbandingan sisi yang berlaku:
$$\bbox[yellow, 5px, border: 2px solid red] {\dfrac{\textbf{AC}}{\textbf{CE}} = \dfrac{\textbf{AB}}{\textbf{DE}} = \dfrac{\textbf{BC}}{\textbf{CD}}}$$
