Contoh Soal 01
Segitiga ABC dan segitiga PQR sama sisi.
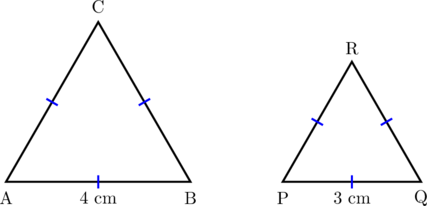
Buktikan bahwa segitiga ABC dan segitiga PQR sebangun.
Cara 1: Dengan menggunakan teorema sudut-sudut (A-A)
Dua buah segitiga dikatakan sebangun jika dua sudut yang bersesuaian pada segitiga pertama dan kedua sama besar.
Karena dalam segitiga sama sisi semua sudut besarnya 60° maka dengan teorema sudut-sudut sudah pasti terpenuhi.
\(\color{blue} \triangle \textbf{ABC} \sim \triangle \textbf{PQR}\)
Cara 2: Dengan menggunakan teorema sisi-sisi-sisi (S-S-S)
Dua buah segitiga dikatakan sebangun jika sisi-sisi yang bersesuaian memiliki perbandingan yang sama.
Karena segitiga ABC sama sisi, maka semua sisi panjangnya 4 cm. Demikian juga untuk segitiga PQR semua sisi panjangnya 3 cm.
\(\dfrac{\textbf{AB}}{\textbf{PQ}} = \dfrac{\textbf{BC}}{\textbf{QR}} = \dfrac{\textbf{CA}}{\textbf{RP}}\)
\(\dfrac{4}{3} = \dfrac{4}{3} = \dfrac{4}{3}\) (perbandingan sisi-sisi yang bersesuaian sama)
\(\color{blue} \triangle \textbf{ABC} \sim \triangle \textbf{PQR}\)
Kesimpulan:
Semua segitiga sama sisi pasti saling sebangun satu dengan yang lainnya.
Contoh Soal 02

Buktikan bahwa segitiga ABC dan segitiga PQR sebangun dan tentukan juga panjang sisi-sisi segitiga yang belum diketahui.
Perhatikan segitiga ABC.
Jumlah sudut dalam suatu segitiga = 180°
\(\angle \textbf{BAC} + \angle \textbf{ACB} + \angle \textbf{CBA} = 180^{\circ}\)
\(53^{\circ} + \angle \textbf{ACB} + 90^{\circ} = 180^{\circ}\)
\(\angle \textbf{ACB} = 90^{\circ}\:-\:53^{\circ} \)
\(\angle \textbf{ACB} = 37^{\circ} \)
Dengan menggunakan teorema sudut-sudut (A-A)
Dua buah segitiga dikatakan sebangun jika dua sudut yang bersesuaian pada segitiga pertama dan kedua sama besar.
Segitiga ABC dan segitiga PQR sama-sama memiliki 2 sudut yang sama besar, yaitu \(\angle \textbf{ACB} = \angle \textbf{QRP} = 37^{\circ} \) dan \(\angle \textbf{CBA} =\angle \textbf{RPQ} = 90^{\circ} \).
Jadi, segitiga ABC sebangun dengan segitiga PQR.
\(\color{blue} \triangle \textbf{ ABC} \sim \triangle \textbf{ PQR}\)
Menentukan panjang sisi-sisi yang belum diketahui
\(\dfrac{\textbf{AB}}{\textbf{PQ}} = \dfrac{\textbf{BC}}{\textbf{QR}} = \dfrac{\textbf{CA}}{\textbf{RP}}\)
\(\dfrac{3}{2} = \dfrac{4}{\textbf{QR}} = \dfrac{\textbf{CA}}{\textbf{RP}}\)
\(\dfrac{3}{2} = \dfrac{4}{\textbf{QR}}\)
kali silang
\(3 \cdot \textbf{QR} = 4 \times 2\)
\(\textbf{QR} = \dfrac{8}{3} \text{ cm}\)
Pada segitiga ABC, untuk menentukan panjang AC dapat menggunakan rumus pythagoras
\(\text{AB}^2 + \text{AC}^2 = \text{AC}^2\)
\(3^2 + 4^2 = \text{AC}^2\)
\(9 + 16= \text{AC}^2\)
\(\text{AC} = \sqrt{25} = 5 \text{ cm}\)
Pada segitiga PQR, untuk menentukan panjang PR dapat menggunakan rumus pythagoras
\(\text{PQ}^2 + \text{QR}^2 = \text{PR}^2\)
\(2^2 + \left(\dfrac{8}{3} \right)^2 = \text{PR}^2\)
\(4 + \dfrac{64}{9}= \text{PR}^2\)
\(\dfrac{36}{9} + \dfrac{64}{9}= \text{PR}^2\)
\( \text{PR}^2 = \dfrac{100}{9}\)
\(\text{PR} = \sqrt{\dfrac{100}{9}}\)
\(\text{PR} = \dfrac{10}{3} \text{ cm}\)
Contoh Soal 03
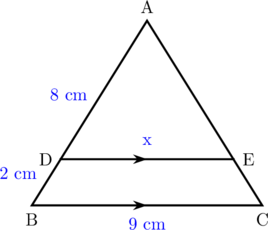
Jika segitiga ADE sebangun dengan segitiga ABC, nilai \(x = \dotso\)
\(\dfrac{\textbf{AD}}{\textbf{AB}} = \dfrac{\textbf{DE}}{\textbf{BC}}\)
\(\dfrac{8}{8 + 2} = \dfrac{x}{9}\)
\(\dfrac{8}{10} = \dfrac{x}{9}\)
Kali silang
\(8 \times 9 = 10x\)
\(72 = 10x\)
\(x = \dfrac{72}{10}\)
\(x = 7,2 \text{ cm}\)
Contoh Soal 04

Jika pajang AB = 11 cm, CD = 6 cm, EF = x cm, dan CE : EA = 3 : 2, nilai \(x = \dotso\)
Tarik garis sejajar dengan DB melalui titik C. Garis tersebut adalah CH.
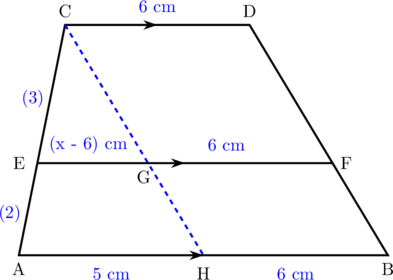
Perhatikan kesebangunan antara segitiga CEG dengan segitiga CAH.
\(\dfrac{\textbf{CE}}{\textbf{CA}} = \dfrac{\textbf{EG}}{\textbf{AH}}\)
\(\dfrac{3}{3 + 2} = \dfrac{x\:-\:6}{5}\)
\(\dfrac{3}{5} = \dfrac{x\:-\:6}{5}\)
Kalikan kedua ruas dengan 5
\(3 = x\:-\:6\)
\(x = 3 + 6\)
\(x = 9\)
Jadi, nilai x = 9.
Contoh Soal 05
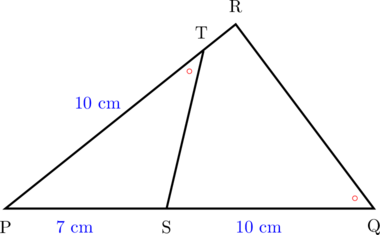
Diketahui \(m\angle \textbf{PTS} = m\angle \textbf{PQR}\), \(\textbf{PS} = 7\text{ cm}\), \(\textbf{SQ} = 10 \text{ cm}\), dan \(\textbf{PT} = 10 \text{ cm}\). Tentukan panjang TR.
Akan dibuktikan bahwa segitiga PTS dan PQR sebangun.
Bukti:
(1) \(m\angle \textbf{PTS} = m\angle \textbf{PQR}\)
(2) \(m\angle \textbf{TPS} = m\angle \textbf{RPQ}\) (sudut yang berhimpit besarnya sama)
Dengan teorema sudut-sudut maka \(\triangle \textbf{PTS} \sim \triangle \textbf{PQR}\)
Karena segitiga PTS dan PQR sebangun, sisi-sisi yang bersesuaian memiliki perbandingan yang sama.
Sisi-sisi yang bersesuaian artinya berada di depan sudut yang sama besar.
\(\dfrac{\textbf{PS}}{\textbf{PR}} = \dfrac{\textbf{PT}}{\textbf{PQ}}\)
\(\dfrac{7}{10 + \textbf{TR}} = \dfrac{10}{7 + 10}\)
\(\dfrac{7}{10 + \textbf{TR}} = \dfrac{10}{17}\)
Kali silang
\(7 \times 17 = 10(10 + \textbf{TR})\)
\(119 = 100 + 10 \textbf{TR}\)
\(119\:-\:100 = 10 \textbf{TR}\)
\(19 = 10 \textbf{TR}\)
\(\textbf{TR} = \dfrac{19}{10} = 1,9 \text{ cm}\)
Jadi, panjang TR adalah \(1,9 \text{ cm}\)
Contoh Soal 06
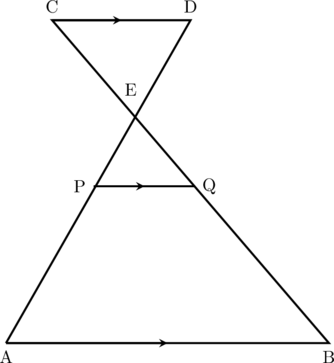
Diketahui CD // PQ // AB, titik P berada di tengah-tengah ruas garis AD, dan Q berada di tengah-tengah ruas garis BC. Jika panjang AB = 14 cm, dan CD = 6 cm, panjang PQ = … cm
(A) 1
(B) 2
(C) 3
(D) 4
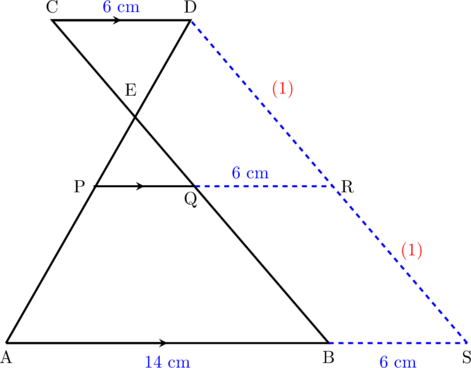
Perhatikan bahwa \(\triangle \textbf{DPR} \sim \triangle \textbf{DAS}\)
\(\dfrac{\textbf{DP}}{\textbf{DA}} = \dfrac{\textbf{DR}}{\textbf{DS}} = \dfrac{\textbf{PR}}{\textbf{AS}}\)
\(\dfrac{1}{2} = \dfrac{\textbf{PQ} + 6}{14 + 6}\)
\(\dfrac{1}{2} = \dfrac{\textbf{PQ} + 6}{20}\)
\(10 = \textbf{PQ} + 6\)
\(\textbf{PQ} = 10 \:-\: 6\)
\(\textbf{PQ} = 4\text{ cm}\)
Jadi, panjang PQ adalah 4 cm.
