KPK adalah singkatan dari Kelipatan Persekutuan Terkecil
Berikut ini adalah cara menentukan KPK dari dua bilangan atau lebih dengan menuliskan kelipatan dari masing-masing bilangan
Contoh 1
Menentukan KPK dari 3 dan 5
Bilangan kelipatan 3 adalah 3, 9, 12, 15, 18, 21, …
Bilangan kelipatan 5 adalah 5, 10, 15, 20, 25, 30, …
Jadi kelipatan persekutuan terkecil dari 3 dan 5 adalah 15
Contoh 2
Menentukan KPK dari 4 dan 7
Bilangan kelipatan 4 adalah 4, 8, 12, 16, 20, 24, 28, 32, …
Bilangan kelipatan 7 adalah 7, 14, 21, 28, 35, 42, …
Jadi kelipatan persekutuan terkecil dari 4 dan 7 adalah 28
Contoh 3
Menentukan KPK dari 3, 5, dan 9
Bilangan kelipatan 3 adalah 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 42, 45, 48, …
Bilangan kelipatan 5 adalah 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, …
Bilangan kelipatan 9 adalah 9, 18, 27, 36, 45, 54, …
Jadi kelipatan persekutuan terkecil dari 2, 5, dan 9 adalah 45
FPB adalah singkatan dari Faktor Persekutuan Terbesar
Berikut ini adalah cara menentukan FPB dari dua bilangan atau lebih dengan menulis semua faktor dari setiap bilangan
Contoh 1
Menentukan FPB dari 6 dan 10
| 6 | |
| 1 | 6 |
| 2 | 3 |
Keterangan:
6 berasal dari 1 × 6
6 berasal dari 2 × 3
| 10 | |
| 1 | 10 |
| 2 | 5 |
Keterangan:
10 berasal dari 1 × 10
10 berasal dari 2 × 5
Semua faktor dari 6 adalah 1, 2, 3, dan 6
Semua faktor dari 10 adalah 1, 2, 5, dan 10
Faktor persekutuan terbesar dari 6 dan 10 adalah 2
Contoh 2
Menentukan FPB dari 12 dan 20
| 12 | |
| 1 | 12 |
| 2 | 6 |
| 3 | 4 |
| 20 | |
| 1 | 20 |
| 2 | 10 |
| 4 | 5 |
Semua faktor dari 12 adalah 1, 2, 3, 4, 6, dan 12
Semua faktor dari 20 adalah 1, 2, 4, 5, 10, dan 20
Faktor persekutuan terbesar dari 12 dan 20 adalah 4
Contoh 3
Menentukan FPB dari 24, 28, dan 36
| 24 | |
| 1 | 24 |
| 2 | 12 |
| 3 | 8 |
| 4 | 6 |
| 28 | |
| 1 | 28 |
| 2 | 14 |
| 4 | 7 |
| 36 | |
| 1 | 36 |
| 2 | 18 |
| 3 | 12 |
| 4 | 9 |
Semua faktor dari 24 adalah 1, 2, 3, 4, 6, 8, 12, dan 24
Semua faktor dari 28 adalah 1, 2, 4, 7, 14, dan 28
Semua faktor dari 36 adalah 1, 2, 3, 4, 9, 12, 18, dan 36
Faktor persekutuan terbesar dari 24, 28, dan 36 adalah 4
Menentukan KPK dan FPB dari dua bilangan atau lebih menggunakan faktorisasi prima
Faktorisasi prima adalah cara menyatakan suatu bilangan dalam bentuk perkalian faktor-faktor primanya
Bilangan prima sendiri adalah bilangan yang hanya memiliki 2 faktor yaitu 1 dan bilangan itu sendiri
Contoh bilangan prima: 2, 3, 5, 7, 11, 13, 17, 19, 23, dan seterusnya
2 merupakan bilangan prima karena hanya memiliki 2 faktor yaitu 1 dan 2
3 merupakan bilangan prima karena hanya memiliki 2 faktor yaitu 1 dan 3
5 merupakan bilangan prima karena hanya memiliki 2 faktor yaitu 1 dan 5
Tentukan KPK dan FPB dari 24 dan 30
Membuat pohon faktor untuk menentukan faktorisasi prima dari 24 dan 30
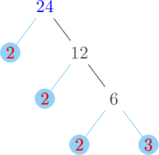
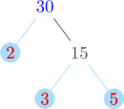
Faktorisasi prima dari 24 = \(2^3 \times 3\)
Faktorisasi prima dari 30 = \(2\times 3 \times 5\)
Untuk KPK pilih semua faktor prima yang ada, untuk faktor prima yang sama pilih pangkat tertinggi
KPK = \(2^3 \times 3 \times 5 = 120\)
Untuk FPB pilih faktor persekutuan prima (faktor prima yang sama) dengan pangkat terendah
FPB = \(2 \times 3 = 6\)
Tentukan KPK dan FPB dari 28 dan 42
Membuat pohon faktor untuk menentukan faktorisasi prima dari 28 dan 42
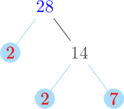
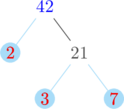
Faktorisasi prima dari 28 = \(2^2 \times 7\)
Faktorisasi prima dari 42 = \(2\times 3 \times 7\)
Untuk KPK pilih semua faktor prima yang ada, untuk faktor prima yang sama pilih pangkat tertinggi
KPK = \(2^2 \times 3 \times 7 = 84\)
Untuk FPB pilih faktor persekutuan prima (faktor prima yang sama) dengan pangkat terendah
FPB = \(2 \times 7 = 14\)
Tentukan KPK dan FPB dari 40, 60, dan 75
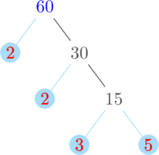
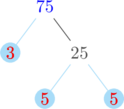
Membuat pohon faktor untuk menentukan faktorisasi prima dari 40, 60, dan 75
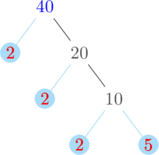
Faktorisasi prima dari 40 = \(2^3 \times 5\)
Faktorisasi prima dari 60 = \(2^2 \times 3 \times 5\)
Faktorisasi prima dari 75 = \( 3 \times 5^2\)
Untuk KPK pilih semua faktor prima yang ada, untuk faktor prima yang sama pilih pangkat tertinggi
KPK = \(2^3 \times 3 \times 5^2 = 600\)
Untuk FPB pilih faktor persekutuan prima (faktor prima yang sama) dengan pangkat terendah
FPB = \(5\)
Tentukan KPK dan FPB dari 102, 125, dan 148
Membuat pohon faktor untuk menentukan faktorisasi prima dari 102, 125, dan 148
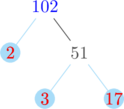
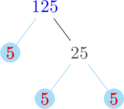
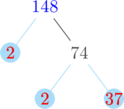
Faktorisasi prima dari 102 = \(2 \times 3 \times 17\)
Faktorisasi prima dari 125 = \(5^3\)
Faktorisasi prima dari 148 = \( 2^2 \times 37\)
Untuk KPK pilih semua faktor prima yang ada, untuk faktor prima yang sama pilih pangkat tertinggi
KPK = \(2^2 \times 3 \times 5^3 \times 17 \times 37\)
Untuk FPB pilih faktor persekutuan prima (faktor prima yang sama) dengan pangkat terendah
Karena 102, 125, dan 148 tidak memiliki faktor persekutuan prima maka nilai FPB nya adalah 1
FPB = \(1\)
