Soal 01
Diketahui keliling suatu lingkaran adalah 44 cm². Luas lingkaran tersebut adalah…
(A) 145 cm²
(B) 154 cm²
(C) 88 cm²
(D) 66 cm²
Jawaban: B
Keliling lingkaran = \(2\pi r\)
\(44 = 2 \cdot \dfrac{22}{7} \cdot r\)
\(\cancel{44} \times \dfrac{7}{\cancel{44}} = r\)
\(r = 7 \text{ cm}\)
Luas lingkaran = \(\pi r^2\)
Luas lingkaran = \(\dfrac{22}{\cancel{7}} \cdot \cancel{7} \cdot 7\)
Luas lingkaran = 154 cm²
Soal 02
Diketahui luas bangun setengah lingkaran adalah 77 cm². Keliling setengah lingkaran tersebut adalah…
(A) 36 cm
(B) 44 cm
(C) 50 cm
(D) 67 cm
Jawaban: A
Luas setengah lingkaran = \(\dfrac{1}{2} \cdot \pi r^2\)
\(77 = \dfrac{1}{\cancel{2}} \cdot \dfrac{\cancelto{11}{22}}{7} \cdot r^2\)
\(\cancelto{7}{77} \times \dfrac{7}{\cancel{11}} = r^2\)
\(r^2 = 49\)
\(r = \sqrt{49} = 7 \text{ cm}\)
Keliling bangun setengah lingkaran = \(r + r + \dfrac{1}{2} \cdot 2\pi r\)
Keliling bangun setengah lingkaran =\(7 + 7 + \dfrac{22}{\cancel{7}} \cdot \cancel{7}\)
Keliling bangun setengah lingkaran = 36 cm
Soal 03
Sebuah taman berbentuk lingkaran dengan ukuran diameter 100 m. Di sekeliling taman tersebut akan ditanami pohon dengan jarak tanam 2 meter. Banyak pohon yang dapat ditanam adalah…
(A) 157
(B) 198
(C) 200
(D) 314
Jawaban: A
Keliling lingkaran = \(\pi \cdot \text{d}\)
Keliling lingkaran = \(3,14 \cdot 100 = 314 \text{ m}\)
Banyak pohon yang dapat ditanam = \(\dfrac{314}{2} = 157 \text { pohon}\)
Soal 04
Sebuah roda sepeda berjari-jari 70 cm telah berputar sebanyak 200 kali. Jarak yang telah ditempuh roda sepeda tersebut adalah…
(A) 590 m
(B) 750 m
(C) 810 m
(D) 880 m
(E) 890 m
Jawaban: D
Jarak yang ditempuh roda = keliling lingkaran × banyak putaran roda
Jarak yang ditempuh roda = \(2 \pi r \times n\)
Jarak yang ditempuh roda = \(2 \cdot \dfrac{22}{7} \cdot 70 \times 200\)
Jarak yang ditempuh roda = \(2 \cdot \dfrac{22}{\cancel{7}} \cdot \cancelto{10}{70} \times 200\)
Jarak yang ditempuh roda = \(88.000 \text{ cm} = 880 \text{ m}\)
Soal 05
Perhatikan gambar di bawah ini.
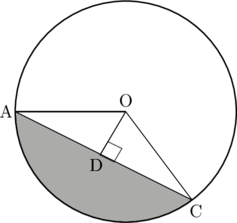
Sebuah lingkaran berjari-jari 13 cm memiliki panjang tali busur AC = 24 cm. Panjang apotema OD adalah…
(A) 3 cm
(B) 4 cm
(C) 5 cm
(D) 8 cm
Jawaban: C
Lihat segitiga siku-siku ODC
Gunakan rumus pythagoras untuk mencari panjang OD
\(\text{OD}^2 + \text{DC}^2 = \text{OC}^2\)
\(\text{OD}^2 + 12^2 = 13^2\)
\(\text{OD}^2 + 144 = 169\)
\(\text{OD}^2 = 169\:-\:144\)
\(\text{OD}^2 = 25\)
\(\text{OD} = \sqrt{25} = 5 \text{ cm}\)
Soal 06
Tiga buah roda identik berjari-jari 42 cm dihubungkan dengan tali seperti gambar di bawah ini.
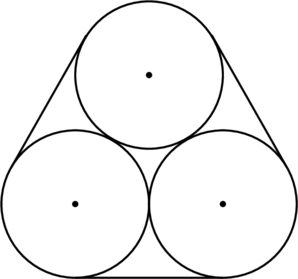
Panjang tali minimum yang dibutuhkan adalah…
(A) 516 cm
(B) 612 cm
(C) 640 cm
(D) 720 cm
Jawaban: A
Panjang tali minimum yang dibutuhkan (L) adalah keliling segitiga sama sisi yang terbentuk dengan menghubungkan ketiga titik pusat lingkaran ditambah dengan 1 keliling lingkaran

\(\text{L} = (3 \times 84) + 2 \cdot \dfrac{22}{\cancel{7}} \cdot \cancelto{6}{42}\)
\(\text{L} = 252 + 264\)
\(\text{L} = 516 \text{ cm}\)
