$$\bbox[yellow, 5px, border: 2px solid red] {\text{Luas Lingkaran} = \pi r^2 \text{ atau } \frac{1}{4} \pi d^2}$$
$$\bbox[yellow, 5px, border: 2px solid red] {\text{Keliling Lingkaran} = 2\pi r \text{ atau } \pi d}$$
ABCD adalah persegi dengan sisi 14 cm. Tentukan luas daerah yang diarsir
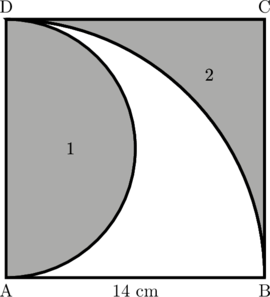
Luas daerah 1 adalah luas setengah lingkaran berdiameter 14 cm
Luas 1 = \(\dfrac{1}{2}\cdot \pi \cdot r^2\)
Luas 1 = \(\dfrac{1}{2} \cdot \dfrac{22}{7} \cdot 7 \cdot 7\)
Luas 1 = \(\dfrac{1}{\cancel{2}} \cdot \dfrac{\cancelto{11}{22}}{\cancel{7}} \cdot \cancel{7} \cdot 7\)
Luas 1 = \(77 \text{ cm}^2\)
Luas daerah 2 sama dengan luas persegi ABCD dikurangi dengan luas seperempat lingkaran besar berjari-jari 14 cm
Luas 2 = \((14 \times 14) \:-\: \dfrac{1}{4} \cdot \dfrac{22}{7} \cdot 14 \cdot 14\)
Luas 2 = \(196 \:-\: \dfrac{1}{4} \cdot \dfrac{22}{\cancel{7}} \cdot \cancelto{2}{14} \cdot 14\)
Luas 2 = \(196 \:-\: 154\)
Luas 2 = \(42 \text{ cm}^2\)
Luas daerah yang diarsir = luas 1 + luas 2
Luas daerah yang diarsir = 77 + 42 = 119 cm²
ABCD adalah persegi dengan sisi 21 cm. Tentukan luas daerah yang diarsir
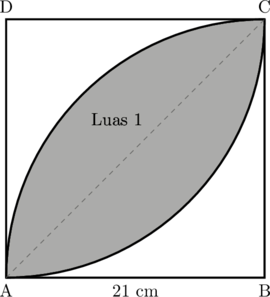
Luas daerah 1 = luas seperempat lingkaran − luas segitiga siku-siku ABC
Luas daerah 1 = \(\dfrac{1}{\cancelto{2}{4}}\cdot \dfrac{\cancelto{11}{22}}{\cancel{7}} \cdot \cancelto{3}{21} \cdot 21 \:-\: \dfrac{1}{2} \cdot 21 \cdot 21\)
Luas daerah 1 = \(\dfrac{693}{2}\:-\: \dfrac{441}{2}\)
Luas daerah 1 = \(\dfrac{252}{2} = 126 \text{ cm}^2\)
Luas daerah yang diarsir = 2 × luas daerah 1
Luas daerah yang diarsir = 2 × \(126 \text{ cm}^2\)
Luas daerah yang diarsir = \(252 \text{ cm}^2\)
Diketahui segitiga siku-siku ABC dengan panjang BC = 12 cm dan AB = 16 cm.
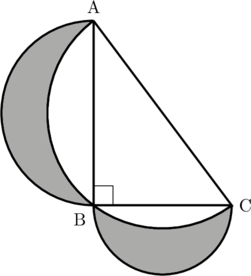
Tentukan luas daerah yang diarsir.
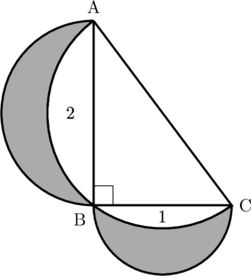
Panjang sisi miring segitiga siku-siku ABC dihitung menggunakan rumus pythagoras.
\(\text{AC}^2 = \text{AB}^2 + \text{BC}^2\)
\(\text{AC}^2 = 16^2 + 12^2\)
\(\text{AC} = \sqrt{400} = 20 \text{ cm}\)
AC menjadi diameter untuk setengah lingkaran yang besar.
Luas daerah 1 dan 2 dapat dicari dengan menghitung luas setengah lingkaran besar berdiameter 20 cm (r = 10 cm) dikurangi luas segitiga siku-siku ABC.
\(\text{L}_1 + \text{L}_2 = \dfrac{1}{2} \cdot \pi \cdot 10^2 \:-\:\dfrac{1}{2} \cdot 12 \cdot 16\)
\(\text{L}_1 + \text{L}_2 = 50\pi \:-\:96 \text{ cm}^2\)
Luas seluruh daerah yang diarsir = luas setengah lingkaran kecil (berdiameter 12 cm) dikurangi luas daerah 1 + luas setengah lingkaran sedang (berdiameter 16 cm) dikurangi luas daerah 2.
atau dapat ditulis:
Luas seluruh daerah yang diarsir = luas setengah lingkaran kecil (berdiameter 12 cm) + luas setengah lingkaran sedang (berdiameter 16 cm) dikurangi luas daerah 1 dan 2.
Luas seluruh daerah yang diarsir = \(\dfrac{1}{2}\cdot \pi \cdot 6^2 + \dfrac{1}{2} \cdot \pi \cdot 8^2 \:-\: (50\pi \:-\:96)\)
Luas seluruh daerah yang diarsir = \(18\pi + 32 \pi \:-\:50 \pi + 96\)
Luas seluruh daerah yang diarsir = \(96 \text{ cm}^2\)
CARA CEPAT:
Luas seluruh daerah yang diarsir = luas segitiga siku-siku ABC
Luas seluruh daerah yang diarsir = \(\dfrac{1}{2} \cdot 12 \cdot 16 = 96 \text{ cm}^2\)
ABCD adalah sebuah persegi dengan sisi 10 cm. Titik A dan D berada pada lingkaran dan BC merupakan garis singgung lingkaran.
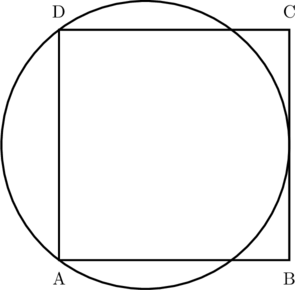
Tentukan luas lingkaran.
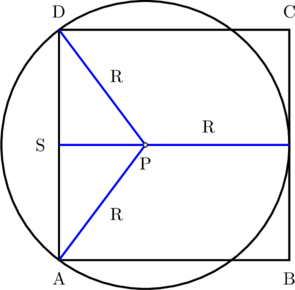
\(\text{PS} = 10 \:-\: \text{R}\)
Lihat \(\triangle \text{ KSP}\)
\(\text{R}^2 = 5^2 + (10\:-\:\text{R})^2\)
\(\cancel{\text{R}^2} = 25 + 100 \:-\:20\text{R} + \cancel{\text{R}^2}\)
\(20\text{R} = 125\)
\(\text{R} = \dfrac{125}{20} = \dfrac{25}{4}\)
\(\text{Luas lingkaran} = \pi \cdot \text{R}^2\)
\(\text{Luas lingkaran} = \dfrac{22}{7} \cdot \left(\dfrac{25}{4} \right)^2\)
\(\text{Luas lingkaran} = \dfrac{22}{7} \cdot \left(\dfrac{625}{16} \right)\)
\(\text{Luas lingkaran} = \dfrac{6875}{56} \text{ cm}^2\)
Perhatikan gambar persegi panjang dengan tiga lingkaran di dalamnya dan menyinggung tiap sisi persegi panjang.
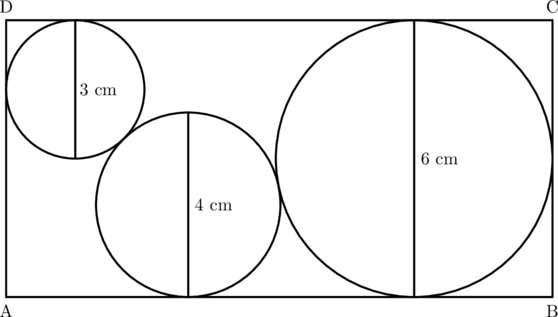
Diameter lingkaran adalah 3 cm, 4 cm, dan 6 cm. Tentukan panjang AB.
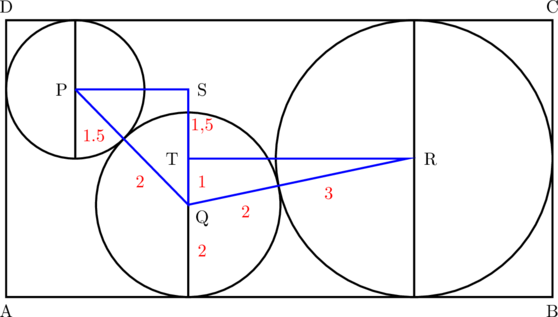
Lihat segitiga siku-siku PSQ
\(\text{PS}^2 = 3,5^2 \:-\:2,5^2\)
\(\text{PS} = \sqrt{\dfrac{49}{4}\:-\:\dfrac{25}{4}}\)
\(\text{PS} = \sqrt{\dfrac{24}{4}}\)
\(\text{PS} = \sqrt{6} \text{ cm}\)
Lihat segitiga siku-siku QTR
\(\text{TR}^2 = 5^2 \:-\:1^2\)
\(\text{TR} = \sqrt{24} = 2\sqrt{6} \text{ cm}\)
\(\text{AB} = 1,5 + \text{PS} + \text{TR} + 3\)
\(\text{AB} = 4,5 + 3\sqrt{6}\)
\(\text{AB} = \dfrac{9 + 6\sqrt{6}}{2} \text{ cm}\)
