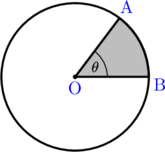
Bila θ dalam satuan derajat, rumusnya:
$$\bbox[yellow, 5px, border: 2px solid red] {\widehat {AB} = \dfrac{\theta}{360^{\circ}} \times 2\pi r}$$
atau
Bila θ dalam satuan radian, rumusnya:
$$\bbox[yellow, 5px, border: 2px solid red] {\widehat {AB} = \theta \cdot r}$$
CONTOH SOAL
Soal 01
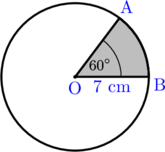
Panjang \(\widehat {AB}= \dotso\)
(A) \(\dfrac{17}{3} \text{ cm}\)
(B) \(\dfrac{19}{3} \text{ cm}\)
(C) \(\dfrac{22}{3} \text{ cm}\)
(D) \(\dfrac{22}{5} \text{ cm}\)
Jawaban: C
\(\widehat {AB}= \dfrac{\theta}{360^{\circ}} \times 2\pi r\)
\(\widehat {AB}= \dfrac{60^{\circ}}{360^{\circ}} \times 2\cdot \dfrac{22}{\cancel{7}} \cdot \cancel{7}\)
\(\widehat {AB}= \dfrac{1}{6} \times 44\)
\(\widehat {AB}= \dfrac{44}{6} = \dfrac{22}{3} \text{ cm}\)
Soal 02
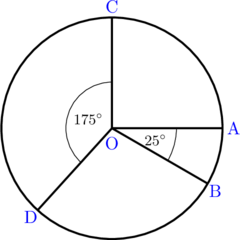
Jika \(\widehat {AB} = 8 \text{ cm}\), maka \(\widehat {CD} = \dotso\)
(A) \(36 \text{ cm}\)
(B) \(42 \text{ cm}\)
(C) \(48 \text{ cm}\)
(D) \(56 \text{ cm}\)
Jawaban: D
\(\dfrac{\widehat {AB}}{\widehat {CD}} = \dfrac{\dfrac{25^{\circ}}{360^{\circ}} \times 2\pi r}{\dfrac{175^{\circ}}{360^{\circ}} \times 2\pi r}\)
\(\dfrac{\widehat {AB}}{\widehat {CD}} = \dfrac{\dfrac{25^{\circ}}{\cancel{360^{\circ}}} \times \cancel{2\pi r}}{\dfrac{175^{\circ}}{\cancel{360^{\circ}}} \times \cancel{2\pi r}}\)
\(\dfrac{8}{\widehat {CD}} = \dfrac{25^{\circ}}{175^{\circ}}\)
\(\dfrac{8}{\widehat {CD}} = \dfrac{1}{7}\)
\(\widehat {CD} = 7 \times 8 = 56 \text{ cm}\)
Soal 03
Diketahui panjang busur suatu lingkaran yang berdiameter 42 cm adalah \(44 \text{ cm}\). Sudut pusat yang menghadap busur lingkaran tersebut besarnya adalah…
(A) \(45^{\circ}\)
(B) \(65^{\circ}\)
(C) \(90^{\circ}\)
(D) \(120^{\circ}\)
Jawaban: D
\(\text{Panjang busur} = \dfrac{\theta}{360^{\circ}} \times 2\pi r\)
\(44 = \dfrac{\theta}{360^{\circ}} \times 2\cdot \dfrac{22}{\cancel{7}} \cdot \cancelto{3}{21}\)
\(44 = \dfrac{\theta}{360^{\circ}} \times 132\)
\(\dfrac{44}{132} = \dfrac{\theta}{360^{\circ}}\)
\(\dfrac{1}{3} = \dfrac{\theta}{360^{\circ}}\)
\(\theta = \dfrac{1}{3} \times 360^{\circ}\)
\(\theta = 120^{\circ}\)
