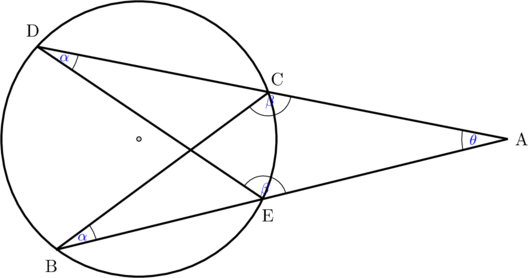
Segitiga ABC dan segitiga ADE sebangun
Bukti:
(1) \(\text{m} \angle \text{ABC} = \text{m} \angle \text{ADE} = \alpha\)
Perhatikan bahwa \(\angle \text{EBC}\) dan \(\angle \text{CDE}\) adalah sudut keliling yang menghadap busur yang sama (busur CE), sehingga kedua sudut tersebut sama besar \((\alpha)\).
(2) \(\text{m} \angle \text{BAC} = \text{m} \angle \text{DAE} = \theta\)
Sudut BAC dan sudut DAE berimpit sehingga keduanya sama besar.
(3) \(\text{m} \angle \text{ACB} = \text{m} \angle \text{AED} = \beta\)
Segitiga ABC dan segitiga ADE sama-sama memiliki memiliki sudut \(\alpha\) dan \(\theta\), maka sudut yang lain pasti sama besar \(\beta\).
Karena semua sudut dalam segitiga ABC dan segitiga ADE sama besar, maka segitiga ABC sebangun dengan segitiga ADE.
Karena sebangun maka perbandingan sisi-sisi yang bersesuaian adalah sama.
\(\dfrac{\text{AB}}{\text{AD}} = \dfrac{\text{AC}}{\text{AE}}\)
Kesimpulan:
$$\bbox[yellow, 5px, border: 2px solid red] {\text{AB} \times \text{AE} = \text{AD} \times \text {AC}}$$

Besar sudut pusat yang menghadap busur BD adalah \(x^{\circ}\)
Besar sudut pusat yang menghadap busur CE adalah \(y^{\circ}\)
$$\bbox[yellow, 5px, border: 2px solid red] {\theta = \dfrac{1}{2}(x^{\circ} \:-\:y^{\circ})}$$
LATIHAN SOAL
SOAL 1
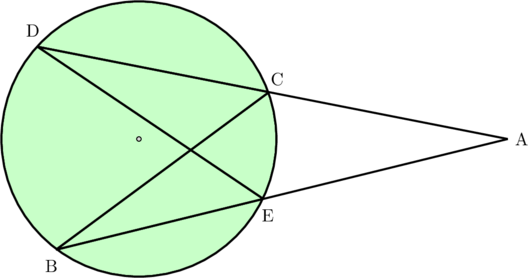
Jika panjang AD = 15 cm, AB = 10 cm, dan AE = 3 cm, tentukan panjang AC.
\(\color{blue} \text{AB} \times \text{AE} = \text{AD} \times \text {AC}\)
\(10 \times 3 = 15 \times \text{AC}\)
\(30 = 15\text{AC}\)
\(\text{AC} = 30 \div 15\)
\(\text{AC} = 2 \text{ cm}\)
Jadi, panjang AC adalah 2 cm
SOAL 2
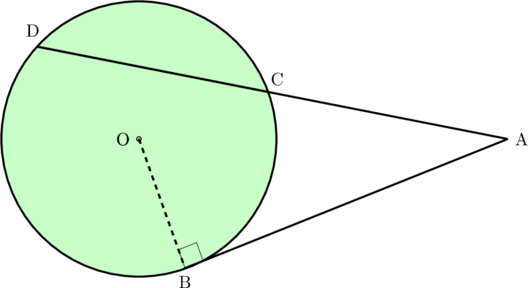
Jika panjang AB = 6 cm dan AD = 9 cm, tentukan panjang AC.
\(\color{blue} \text{AB} \times \text{AB} = \text{AC} \times \text {AD}\)
\(\text{AB}^2 = \text{AC} \times 9\)
\(6^2 = \text{AC}\times 9\)
\(36 = 9\text{AC}\)
\(\text{AC} = 36 \div 9 \text{ cm}\)
\(\text{AC} = 4 \text{ cm}\)
Jadi, panjang AC adalah 4 cm
SOAL 3

Besar sudut pusat yang menghadap busur BD adalah \(110^{\circ}\)
Besar sudut pusat yang menghadap busur CE adalah \(40^{\circ}\)
Tentukan \(\theta\)
\(\theta = \dfrac{1}{2}(110^{\circ} \:-\:40^{\circ})\)
\(\theta = \dfrac{1}{2}\cdot 70^{\circ}\)
\(\theta = 35^{\circ}\)
