Segi empat tali busur adalah segi empat yang setiap titik sudutnya berada pada lingkaran.
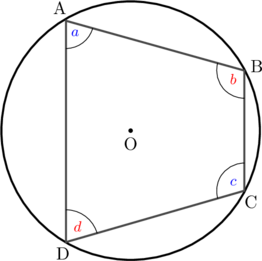
Dalam segi empat tali busur, jumlah sudut yang saling berhadapan 180°.
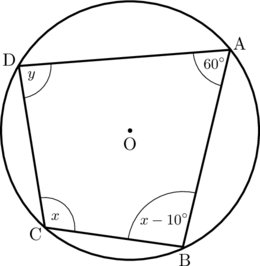
Pada segi empat tali busur ABCD di atas tentukan nilai \(x\) dan \(y\).
Sudut BAD dan sudut BCD saling berhadapan sehingga berlaku:
\(\text{m}\angle \text{BAD} + \text{m}\angle \text{BCD} = 180^{\circ}\)
\(60^{\circ} + x = 180^{\circ}\)
\(x = 180^{\circ}\:-\: 60^{\circ}\)
\(x = 120^{\circ}\)
Sudut ADC dan sudut ABC saling berhadapan sehingga berlaku:
\(\text{m}\angle \text{ADC} + \text{m}\angle \text{ABC} = 180^{\circ}\)
\(y + x\:-\:10^{\circ} = 180^{\circ}\)
\(y + x = 190^{\circ}\)
\(y + 120^{\circ} = 190^{\circ}\)
\(y = 190^{\circ}\:-\:120^{\circ}\)
\(y = 70^{\circ}\)
Pada segi empat tali busur ABCD di atas tentukan nilai \(x\) dan \(y\).
Sudut BAD dan sudut BCD saling berhadapan sehingga berlaku:
\(\text{m}\angle \text{BAD} + \text{m}\angle \text{BCD} = 180^{\circ}\)
\(50^{\circ} + x + 4y = 180^{\circ}\)
\(x + 4y = 180^{\circ}\:-\:50^{\circ}\)
\(x + 4y = 130^{\circ}\dotso \color{blue} (1)\)
Sudut ABC dan sudut ADC saling berhadapan sehingga berlaku:
\(\text{m}\angle \text{ABC} + \text{m}\angle \text{ADC} = 180^{\circ}\)
\(2x + 4y = 180^{\circ}\dotso \color{blue} (2)\)
Kurangkan persamaan (2) dengan persamaan (1),
\(2x + 4y = 180^{\circ}\dotso \color{blue} (2)\)
\(x + 4y = 130^{\circ}\dotso \color{blue} (1)\)
\(x = 50^{\circ}\)
\(x + 4y = 130^{\circ}\)
\(50^{\circ} + 4y = 130^{\circ}\)
\(4y = 130^{\circ}\:-\:50^{\circ}\)
\(4y = 80^{\circ}\)
\(y = 80^{\circ}\div 4\)
\(y = 20^{\circ}\)
