Soal 1
Perhatikan gambar berikut:
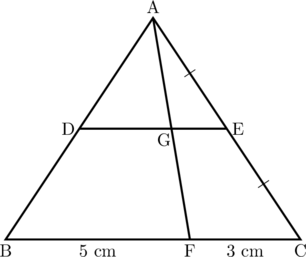
Pada segitiga ABC diketahui panjang BF = 5 cm, FC = 3 cm, dan panjang AE sama dengan panjang EC. DE sejajar dengan BC. Perbandingan luas segitiga ADG dengan luas segitiga AFC adalah ..
(A) 19 : 22
(B) 20 : 37
(C) 25 : 36
(D) 28 : 39
Jawaban: C
Langkah 1: menghitung panjang GE
Perhatikan segitiga AGE dan segitiga AFC
\(\color{blue}\triangle \text{AGE} \text{ sebangun dengan } \triangle \text{AFC}\)
Panjang sisi-sisi yang bersesuaian mempunyai perbandingan yang sama

\(\dfrac{\text{AE}}{\text{AC}} = \dfrac{\text{GE}}{\text{FC}}\)
\(\dfrac{1}{2} = \dfrac{\text{GE}}{3}\)
Kalikan silang,
\(1 \times 3 = 2 \times \text{GE}\)
\(3 = 2 \times \text{GE}\)
\(\text{GE} = \dfrac{3}{2} = 1,5 \text{ cm}\)
Langkah 2: menghitung panjang DE
Perhatikan segitiga ADE dan segitiga ABC
\(\color{blue}\triangle \text{ADE} \text{ sebangun dengan } \triangle \text{ABC}\)
Panjang sisi-sisi yang bersesuaian mempunyai perbandingan yang sama

\(\dfrac{\text{AE}}{\text{AC}} = \dfrac{\text{DE}}{\text{BC}}\)
\(\dfrac{1}{2} = \dfrac{\text{DE}}{8}\)
Kalikan silang,
\(1 \times 8 = 2 \times \text{DE}\)
\(8 = 2 \times \text{DE}\)
\(\text{DE} = \dfrac{8}{2} = 4 \text{ cm}\)
Langkah 3: menghitung panjang DG
DG = DE − GE
DG = 4 − 1,5
DG = 2,5 cm
Langkah 4: menghitung perbandingan luas segitiga ADG dengan luas segitiga AFC
Perbandingan luas dua segitiga yang sebangun sama dengan kuadrat perbandingan panjang alas kedua segitiga.
\(\dfrac{\text{luas segitiga ADG}}{\text{luas segitiga AFC}} = \left(\dfrac{\text{DG}}{\text{FC}}\right)^2\)
\(\dfrac{\text{luas segitiga ADG}}{\text{luas segitiga AFC}} = \left(\dfrac{2,5}{3}\right)^2\)
\(\dfrac{\text{luas segitiga ADG}}{\text{luas segitiga AFC}} = \left(\dfrac{\frac{5}{2}}{3}\right)^2\)
\(\dfrac{\text{luas segitiga ADG}}{\text{luas segitiga AFC}} = \left(\dfrac{5}{6}\right)^2\)
\(\dfrac{\text{luas segitiga ADG}}{\text{luas segitiga AFC}} = \dfrac{25}{36}\)
Jadi, perbandingan luas segitiga ADG dengan luas segitiga AFC = 25 : 36
Soal 2
Empat puluh persen peserta didik di suatu sekolah adalah laki-laki. Sebanyak 10% laki-laki memakai kacamata dan 60% perempuan tidak memakai kacamata. Jika diketahui ada 154 siswa yang memakai kacamata, maka jumlah seluruh peserta didik di sekolah tersebut adalah … orang
(A) 450
(B) 550
(C) 580
(D) 600
Jawaban: B
Jumlah peserta didik:
- laki-laki = 40%
- Perempuan = 100% − 40% = 60%
Sebanyak 10% laki-laki memakai kacamata
60% perempuan tidak memakai kacamata, artinya ada 40% perempuan memakai kacamata
Misal jumlah seluruh peserta didik di sekolah tersebut adalah \(\textbf{T}\)
Laki-laki berkacamata + perempuan berkacamata = 154 orang
10% × 40% × \(\textbf{T}\) + 40% × 60% × \(\textbf{T}\) = 154 orang
\(\dfrac{10}{100}\cdot \dfrac{40}{100}\cdot \textbf{T} + \dfrac{40}{100}\cdot \dfrac{60}{100}\cdot \textbf{T} = 154\)
\(\dfrac{400}{10000}\textbf{T} + \dfrac{2400}{10000}\textbf{T} = 154\)
\(\dfrac{4}{100}\textbf{T} + \dfrac{24}{100}\textbf{T} = 154\)
\(\dfrac{28}{100}\textbf{T}= 154\)
\(\textbf{T} = \dfrac{100}{28}\times 154\)
\(\textbf{T} = \dfrac{100}{\cancel{28}}\times \cancelto{5,5}{154}\)
\(\textbf{T} = 100 \times 5,5 = 550\)
Jadi, jumlah seluruh peserta didik di sekolah tersebut adalah 550 orang
Soal 3
Pak Rahmat memiliki 60 permen rasa jeruk, 40 permen rasa mangga, dan 50 permen rasa durian. Permen-permen tersebut akan dibagikan Pak Rahmat kepada para muridnya. Setiap murid mendapatkan permen setiap rasa sama banyak. Banyaknya permen rasa jeruk yang diterima setiap murid adalah …
(A) 5
(B) 6
(C) 8
(D) 10
Jawaban: B
Langkah 1 : Mencari FPB dari 60, 40, dan 50
Faktorisasi prima dari 60 = 2² × 3 × 5
Faktorisasi prima dari 40 = 2³ × 5
Faktorisasi prima dari 50 = 2 × 5²
FPB dari 60, 40, dan 50 adalah 10
Karena FPB = 10, artinya ada 10 murid yang mendapatkan permen setiap rasa sama banyak
Langkah 2 : Menghitung jumlah permen rasa jeruk yang diterima setiap murid
Jumlah permen jeruk yang diterima setiap murid = 60 permen ÷ 10 = 6 permen rasa jeruk
Soal 4
Segitiga ABC adalah segitiga sama sisi, dengan panjang AB = AC.
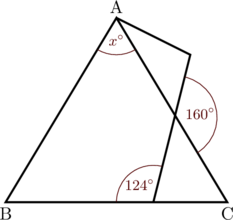
Nilai \(x\) yang benar adalah …
(A) 12
(B) 14
(C) 16
(D) 20
Jawaban: A
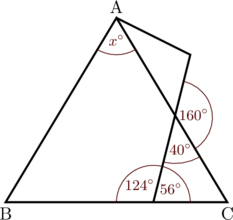
Jumlah semua sudut dalam sebuah segitiga adalah 180°
Besar sudut ACB = 180° − 40° − 56° = 84°
Karena segitiga ABC adalah sama kaki, maka besar sudut ABC = ACB = 84°
Besar sudut BAC = 180° − 84° − 84°
\(x^{\circ}\) = 180° − 84° − 84° = 12°
Jadi, nilai \(x\) adalah 12
Soal 5
OSN 2017
Diberikan empat bilangan asli \(a, b, c, \text{ dan } d\). Jika KPK \((a, b, c) = 30\), \(3a = 2b\), \(c = 15\), KPK \((a, b) = d\), maka nilai maksimum dari \(\dfrac{1}{a} + \dfrac{1}{b} + \dfrac{1}{c} + \dfrac{1}{d}\) adalah …
Faktorisasi prima dari \(c = 3 \times 5\)
Karena KPK \((a, b, c) = 30\) dan \(3a = 2b\), maka kemungkinan nilai \(a\) dan \(b\) adalah:
\(a = 2\)
\(b = 3\)
Selanjutnya,
KPK \((a, b) = d\)
KPK \((2, 3) = 6\)
\(\dfrac{1}{a} + \dfrac{1}{b} + \dfrac{1}{c} + \dfrac{1}{d}\)
\(\dfrac{1}{2} + \dfrac{1}{3} + \dfrac{1}{15} + \dfrac{1}{6}\)
\(\dfrac{15}{30} + \dfrac{10}{30} + \dfrac{2}{30} + \dfrac{5}{30}\)
\(\dfrac{15 + 10 + 2 + 5}{30}\)
\(\dfrac{32}{30}\)
\(\dfrac{16}{15}\)
\(1\dfrac{1}{15}\)
Jadi, \(\dfrac{1}{a} + \dfrac{1}{b} + \dfrac{1}{c} + \dfrac{1}{d} = 1\dfrac{1}{15}\)
Soal 6
OSN 2017
The value of \(\dfrac{100001^2\:-\:99999^2}{1001^2\:-\:999^2}\) is …
\(\dfrac{100001^2\:-\:99999^2}{1001^2\:-\:999^2}\)
dapat ditulis menjadi:
\(\dfrac{(100000 + 1)^2\:-\:(100000\:-\:1)^2}{(1000 + 1)^2\:-\:(1000\:-\:1)^2}\)
Bentuk \(\color{blue} \text{A}^2\:-\:\text{B}^2 = (\text{A} + \text{B})(\text{A}\:-\:\text{B})\)
\(\dfrac{(100000 + 1 + 100000\:-\:1)(100000 + 1 \:-\: (100000\:-\:1))}{(1000 + 1 + 1000 \:-\:1)(1000 + 1 \:-\:(1000 \:-\:1))}\)
\(\dfrac{(200000)(2)}{(2000)(2)}\)
\(\dfrac{400000}{4000}\)
\(100\)
Jadi, \(\dfrac{100001^2\:-\:99999^2}{1001^2\:-\:999^2} = 100\)
Soal 7
Berikut ini adalah data mata pelajaran yang paling disukai oleh sekelompok siswa di suatu sekolah.
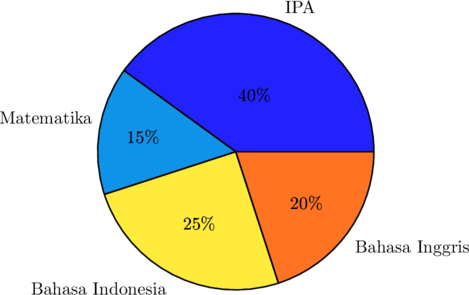
Jika banyaknya siswa yang menyukai pelajaran matematika adalah 9 orang, maka banyaknya siswa dalam kelompok tersebut adalah … orang
(A) 40
(B) 50
(C) 55
(D) 60
Jawaban: D
Siswa yang menyukai matematika sebanyak 15% = 9 orang
Banyak siswa dalam kelompok tersebut adalah \(\dfrac{100}{15} \times 9 \text{ orang} = 60 \text{ orang}\)
