Diketahui titik A, B, dan C terletak pada ruas garis yang sama.
Vektor posisi titik A, B, dan C berturut-turut adalah \(\textbf{a}\), \(\textbf{b}\), dan \(\textbf{c}\).
Titik C berada diantara titik A dan B dalam perbandingan AC : CB = m : n.
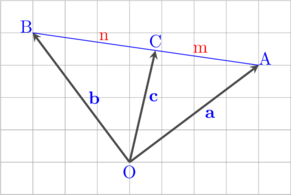
Vektor posisi \(\textbf{c}\) dapat dicari sebagai berikut:
\(\textbf{c} = \dfrac{m\textbf{b} + n\textbf{a} }{m + n}\)
Contoh Soal
Soal 1
Diketahui koordinat titik A(4, 3) dan B(-3, 4). Titik C berada pada ruas garis AB, dengan perbandingan \(\text{AC} : \text{CB} = 1 : 3\). Tentukan koordinat titik C tersebut.
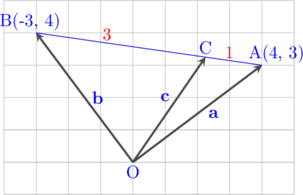
Diketahui:
\(\textbf{a} = \left(\begin{array}{c}4\\ 3\end{array}\right)\)
\(\textbf{b} = \left(\begin{array}{c}-3\\ 4\end{array}\right)\)
\(\text{AC} : \text{CB} = m : n = 1 : 3\)
Vektor posisi \(\textbf{c}\) dapat dicari sebagai berikut:
\(\textbf{c} = \dfrac{m\textbf{b} + n\textbf{a} }{m + n}\)
\(\textbf{c} = \dfrac{1\cdot \left(\begin{array}{c}-3\\ 4\end{array}\right) + 3\cdot\left(\begin{array}{c}4\\ 3\end{array}\right)}{1 + 3}\)
\(\textbf{c} = \dfrac{\left(\begin{array}{c}-3\\ 4\end{array}\right) + \left(\begin{array}{c}12\\ 9\end{array}\right)}{4}\)
\(\textbf{c} = \dfrac{\left(\begin{array}{c}-3 + 12\\ 4 + 9\end{array}\right)}{4}\)
\(\textbf{c} = \dfrac{\left(\begin{array}{c}9\\ 13\end{array}\right)}{4}\)
\(\textbf{c} = \left(\begin{array}{c}\frac{9}{4}\\ \frac{13}{4}\end{array}\right)\)
Jadi koordinat titik C adalah \((\frac{9}{4},\:\frac{13}{4})\)
Soal 2
Perhatikan gambar di bawah ini:
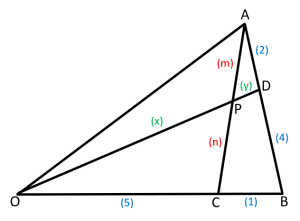
Diketahui OC : CB = 5 : 1 dan BD : DA = 4 : 2. Garis OD berpotongan dengan garis AC di titik P sehingga OP : PD = x : y dan AP : PC = m : n. Tentukan:
(A) x : y
(B) m : n
Langkah 1: Nyatakan vektor posisi \(\overrightarrow{\text{OD}}\)
\(\overrightarrow{\text{OD}}= \dfrac{2\cdot \overrightarrow{\text{OB}} + 4\cdot \overrightarrow{\text{OA}}}{2 + 4}\)
\(\overrightarrow{\text{OD}}= \dfrac{2\cdot \overrightarrow{\text{OB}} + 4\cdot \overrightarrow{\text{OA}}}{6}\)
Langkah 2: Nyatakan vektor \(\overrightarrow{\text{AC}}\)
\(\overrightarrow{\text{AC}}= \dfrac{5\cdot \overrightarrow{\text{AB}} + 1\cdot \overrightarrow{\text{AO}}}{5+1}\)
\(\overrightarrow{\text{AC}}= \dfrac{5\cdot \overrightarrow{\text{AB}} + 1\cdot \overrightarrow{\text{AO}}}{6}\)
\(\text{Note:}\)
\(\color{blue} \overrightarrow{\text{OA}} + \overrightarrow{\text{AB}} =\color{blue} \overrightarrow{\text{OB}}\)
\(\color{blue} \overrightarrow{\text{AB}} =\color{blue} \overrightarrow{\text{OB}}\:-\:\overrightarrow{\text{OA}}\)
\(\overrightarrow{\text{AC}}= \dfrac{5\cdot (\overrightarrow{\text{OB}}\:-\:\overrightarrow{\text{OA}})+ 1\cdot \overrightarrow{\text{AO}}}{6}\)
\(\overrightarrow{\text{AC}}= \dfrac{5\cdot (\overrightarrow{\text{OB}}\:-\:\overrightarrow{\text{OA}})\:-\: \overrightarrow{\text{OA}}}{6}\)
\(\overrightarrow{\text{AC}}= \dfrac{5\cdot\overrightarrow{\text{OB}}\:-\:6\cdot\overrightarrow{\text{OA}}}{6}\)
Langkah 3: \(\overrightarrow{\text{OA}} = \overrightarrow{\text{OP}} + \overrightarrow{\text{PA}}\)
\(\overrightarrow{\text{OP}} = \dfrac{x}{x + y}\cdot \overrightarrow{\text{OD}}\)
\(\overrightarrow{\text{PA}} = \dfrac{m}{m + n}\cdot \overrightarrow{\text{CA}}\)
\(\overrightarrow{\text{PA}} = -\dfrac{m}{m + n}\cdot \overrightarrow{\text{AC}}\)
\(\overrightarrow{\text{OA}} = \dfrac{x}{x + y}\cdot \overrightarrow{\text{OD}} \:-\: \dfrac{m}{m + n}\cdot \overrightarrow{\text{AC}}\)
\(\overrightarrow{\text{OA}} = \dfrac{x}{x + y}\left(\dfrac{2\cdot \overrightarrow{\text{OB}} + 4\cdot \overrightarrow{\text{OA}}}{6}\right) \:-\: \dfrac{m}{m + n}\left(\dfrac{5\cdot\overrightarrow{\text{OB}}\:-\:6\cdot\overrightarrow{\text{OA}}}{6}\right)\)
\(\textbf{a} = \dfrac{x}{x + y}\left(\dfrac{\textbf{b} + 2\textbf{a}}{3}\right) \:-\: \dfrac{m}{m + n}\left(\dfrac{5\textbf{b}\:-\:6\textbf{a}}{6}\right)\)
\(\textbf{a} =\dfrac{x}{3(x+y)}\textbf{b} + \dfrac{2x}{3(x + y)}\textbf{a}\:-\:\dfrac{5m}{6(m +n)}\textbf{b} + \dfrac{m}{m+n}\textbf{a}\)
\(0\textbf{b} + 1\textbf{a} =\dfrac{x}{3(x+y)}\textbf{b} \:-\:\dfrac{5m}{6(m +n)}\textbf{b} + \dfrac{2x}{3(x + y)}\textbf{a}+ \dfrac{m}{m+n}\textbf{a}\)
Samakan koefisien dari masing-masing vektor
\(0 = \dfrac{x}{3(x+y)}\:-\:\dfrac{5m}{6(m +n)}\dotso\dotso\color{blue}(1)\)
\(1 = \dfrac{2x}{3(x + y)} + \dfrac{m}{m+n}\dotso\dotso\color{blue}(2)\)
Selanjutnya eliminasi kedua persamaan tersebut
Persamaan pertama dikali 2, persamaan kedua dikali 1
\(0 = \dfrac{2x}{3(x+y)}\:-\:\dfrac{10m}{6(m +n)}\dotso\dotso\color{blue}(1)\)
\(1 = \dfrac{2x}{3(x + y)} + \dfrac{m}{m+n}\dotso\dotso\color{blue}(2)\)
Kurangkan persamaan (1) dengan persamaan (2)
\(-1 = -\dfrac{8}{3}\cdot \dfrac{m}{m+n}\)
\(1 = \dfrac{8m}{3(m+n)}\)
\(3(m + n) = 8m\)
\(3m + 3n = 8m\)
\(3n = 5m\)
\(\dfrac{3}{5} = \dfrac{m}{n}\)
Jadi m : n = 3 : 5
Dengan menggunakan cara eliminasi lagi
Persamaan pertama dikali 1, persamaan kedua dikali \(\frac{5}{6}\)
\(0 = \dfrac{x}{3(x+y)} \:-\:\dfrac{5m}{6(m + n)}\)
\(\dfrac{5}{6} = \dfrac{10x}{18(x + y)} + \dfrac{5m}{6(m + n)}\)
Jumlahkan persamaan pertama dengan persamaan kedua
\(\dfrac{5}{6} = \dfrac{8x}{9(x + y)}\)
\(45(x + y) = 48x\)
\(45x + 45y = 48x\)
\(45y = 3x\)
\(15y = x\)
\(\dfrac{x}{y} = \dfrac{15}{1}\)
Jadi x : y = 15 : 1
