Perhatikan gambar kubus ABCD.EFGH berikut:
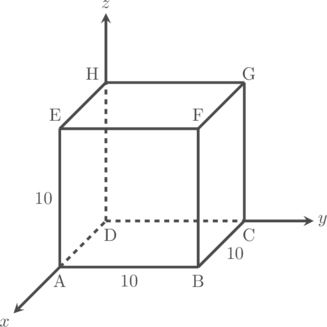
Diketahui kubus ABCD.EFGH memiliki rusuk dengan panjang 10 satuan.
- \(\overrightarrow{\text{DA}}= 10\textbf{i} \text{ dan } \overrightarrow{\text{AD}}= -10\textbf{i} \)
- \(\overrightarrow{\text{DC}}= 10\textbf{j} \text{ dan } \overrightarrow{\text{CD}}= -10\textbf{j} \)
- \(\overrightarrow{\text{DH}}= 10\textbf{k} \text{ dan } \overrightarrow{\text{HD}}= -10\textbf{k} \)
Dari informasi di atas, nyatakan:
A. Vektor \(\overrightarrow{\text{DB}}\) dan panjang DB
B. Vektor\(\overrightarrow{\text{DF}}\) dan panjang DF
C. Vektor \(\overrightarrow{\text{AC}}\) dan panjang AC
D. Vektor \(\overrightarrow{\text{AG}}\) dan panjang AG
Penyelesaian:
Menyatakan vektor \(\overrightarrow{\text{DB}}\)
\(\overrightarrow{\text{DB}} = \overrightarrow{\text{DA}} + \overrightarrow{\text{AB}}\)
\(\overrightarrow{\text{DB}} = 10\textbf{i} + 10\textbf{j}\)
\(\text{DB} = \sqrt{10^2 + 10^2} = \sqrt{200} = 10\sqrt{2}\text{ satuan}\)
Menyatakan vektor \(\overrightarrow{\text{DF}}\)
\(\overrightarrow{\text{DF}} = \overrightarrow{\text{DB}} + \overrightarrow{\text{BF}}\)
\(\overrightarrow{\text{DF}} = 10\textbf{i} + 10\textbf{j} + 10\textbf{k}\)
\(\text{DF} = \sqrt{10^2 + 10^2 + 10^2} = \sqrt{300} = 10\sqrt{3}\text{ satuan}\)
Menyatakan vektor \(\overrightarrow{\text{AC}}\)
\(\overrightarrow{\text{AC}} = \overrightarrow{\text{AB}} + \overrightarrow{\text{BC}}\)
\(\overrightarrow{\text{AC}} = 10\textbf{j} \:-\: 10\textbf{i}\)
\(\text{AC} = \sqrt{10^2 + (-10)^2} = \sqrt{200} = 10\sqrt{2}\text{ satuan}\)
Menyatakan vektor \(\overrightarrow{\text{AG}}\)
\(\overrightarrow{\text{AG}} = \overrightarrow{\text{AC}} + \overrightarrow{\text{CG}}\)
\(\overrightarrow{\text{AG}} = 10\textbf{j} \:-\: 10\textbf{i} + 10\textbf{k}\)
\(\text{AG} = \sqrt{10^2 + (-10)^2 + 10^2} = \sqrt{300} = 10\sqrt{3}\text{ satuan}\)
Contoh Soal
Soal 1
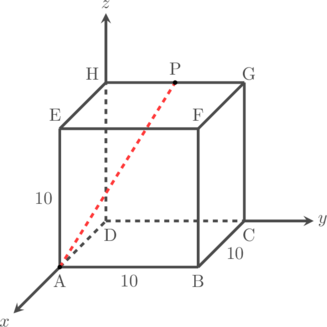
Kubus ABCD.EFGH memiliki panjang rusuk 10 satuan. Titik P terletak di tengah HG. Tentukan panjang AP.
Cara 1:
Sebelum menentukan panjang AP, terlebih dahulu kita nyatakan vektor \(\overrightarrow{\text{AP}}\)
\(\overrightarrow{\text{AP}} = \overrightarrow{\text{AB}} + \overrightarrow{\text{BC}} + \overrightarrow{\text{CG}} + \overrightarrow{\text{GP}}\)
\(\overrightarrow{\text{AP}} = 10\textbf{j} \:-\: 10\textbf{i} + 10\textbf{k} + \frac{1}{2}\cdot \overrightarrow{\text{GH}}\)
\(\overrightarrow{\text{AP}} = 10\textbf{j} \:-\: 10\textbf{i} + 10\textbf{k} + \frac{1}{2}\cdot (-10)\textbf{j} \)
\(\overrightarrow{\text{AP}} = 10\textbf{j} \:-\: 10\textbf{i} + 10\textbf{k} \:-\:5\textbf{j} \)
\(\overrightarrow{\text{AP}} = -10\textbf{i} + 5\textbf{j} + 10\textbf{k} \)
Menghitung panjang AP
\(||\overrightarrow{\text{AP}}|| = \sqrt{(-10)^2 + 5^2 + 10^2}\)
\(||\overrightarrow{\text{AP}}|| = \sqrt{100 + 25 + 100}\)
\(||\overrightarrow{\text{AP}}|| = \sqrt{225}\)
\(||\overrightarrow{\text{AP}}|| = 15\text { satuan}\)
Cara 2:
Tentukan koordinat titik A dan P terlebih dahulu
Koordinat titik A adalah \((10, 0, 0)\) dan koordinat titik P adalah \((0, 5, 10)\)
\(\overrightarrow{\text{AP}} = \textbf{p}\:-\:\textbf{a}\)
\(\overrightarrow{\text{AP}} = \left(\begin{array}{c}0\\ 5\\10\end{array}\right)\:-\:\left(\begin{array}{c}10\\ 0\\0\end{array}\right) = \left(\begin{array}{c}-10\\ 5\\10\end{array}\right)\)
\(||\overrightarrow{\text{AP}}|| =\sqrt{(-10)^2 + 5^2 + 10^2}\)
\(||\overrightarrow{\text{AP}}|| =\sqrt{100 + 25 + 100}\)
\(||\overrightarrow{\text{AP}}|| =\sqrt{225}\)
\(||\overrightarrow{\text{AP}}|| = 15\text { satuan}\)
Soal 2
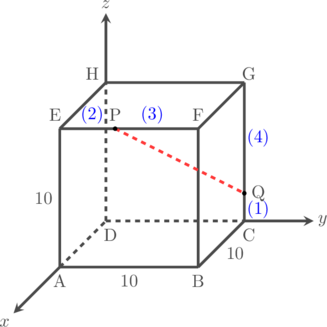
Kubus ABCD.EFGH memiliki panjang rusuk 10 satuan. Titik P terletak pada EF dengan perbandingan EP : PF = 2 : 3. Titik Q terletak pada CG dengan perbandingan CQ : QG = 1 : 4. Tentukan panjang PQ.
Cara 1:
Sebelum menentukan panjang PQ, terlebih dahulu kita nyatakan vektor \(\overrightarrow{\text{PQ}}\)
\(\overrightarrow{\text{PQ}} = \overrightarrow{\text{PF}} + \overrightarrow{\text{FB}} + \overrightarrow{\text{BC}} + \overrightarrow{\text{CQ}}\)
\(\overrightarrow{\text{PQ}} = \frac{3}{5}\cdot \overrightarrow{\text{EF}} + \overrightarrow{\text{FB}} + \overrightarrow{\text{BC}} + \frac{1}{5}\cdot \overrightarrow{\text{CG}}\)
\(\overrightarrow{\text{PQ}} = \frac{3}{5}\cdot 10\textbf{j} \:-\:10\textbf{k}\:-\:10\textbf{i} + \frac{1}{5}\cdot 10\textbf{k}\)
\(\overrightarrow{\text{PQ}} = 6\textbf{j} \:-\:10\textbf{k}\:-\:10\textbf{i} + 2\textbf{k}\)
\(\overrightarrow{\text{PQ}} = -10\textbf{i} + 6\textbf{j} \:-\:8\textbf{k}\)
Menghitung panjang PQ
\(||\overrightarrow{\text{PQ}}|| = \sqrt{(-10)^2 + 6^2 + (-8)^2}\)
\(||\overrightarrow{\text{PQ}}|| = \sqrt{100 + 36 + 64}\)
\(||\overrightarrow{\text{PQ}}|| = \sqrt{200}\)
\(||\overrightarrow{\text{PQ}}|| = 10\sqrt{2}\text { satuan}\)
Cara 2:
Tentukan koordinat titik P dan Q terlebih dahulu
Koordinat titik P adalah \((10, 4, 10)\) dan koordinat titik Q adalah \((0, 10, 2)\)
\(\overrightarrow{\text{PQ}} = \textbf{q}\:-\:\textbf{p}\)
\(\overrightarrow{\text{AP}} = \left(\begin{array}{c}0\\10\\2\end{array}\right)\:-\:\left(\begin{array}{c}10\\ 4\\10\end{array}\right) = \left(\begin{array}{c}-10\\6\\-8\end{array}\right)\)
\(||\overrightarrow{\text{PQ}}|| =\sqrt{(-10)^2 + 6^2 + (-8)^2}\)
\(||\overrightarrow{\text{PQ}}|| =\sqrt{100 + 36 + 64}\)
\(||\overrightarrow{\text{PQ}}|| =\sqrt{200}\)
\(||\overrightarrow{\text{PQ}}|| = 10\sqrt{2}\text { satuan}\)
