$$\bbox[yellow, 5px, border: 2px solid red] {\textbf{P(A)} = \dfrac{\text{n(A)}}{\text{n(S)}}}$$
$$\bbox[yellow, 5px, border: 2px solid red] {\textbf{P(A)} = 1 \:-\: \textbf{P}\text{(A)}^{\text{c}}}$$
Keterangan:
P(A) = peluang kejadian A
n(A) = banyaknya kemungkinan kejadian A
n(S) = banyaknya titik sampel
\(\color{green} \textbf{P}\text{(A)}^{\text{c}}\) = peluang kejadian bukan A
Peluang Kejadian Majemuk
Dua kejadian yang tidak saling memengaruhi.
\(\color{blue} \text{P}(\text{A} \cap \text{B}) = \text{P(A)} \times \text{P(B)}\)
Dua kejadian yang tidak mungkin terjadi secara bersamaan (tidak memiliki irisan)
\(\color{blue} \text{P}(\text{A} \cap \text{B}) = 0\)

Dua kejadian yang dapat terjadi secara bersamaan (memiliki irisan)
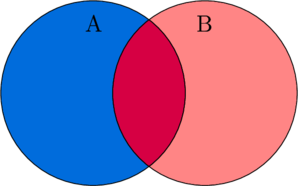
Menghitung Peluang Gabungan Dua Kejadian
P(A ∪ B) = P(A) + P(B) − P(A ∩ B)
Menghitung Peluang Gabungan Tiga Kejadian
P(A ∪ B ∪ C) = P(A) + P(B) + P(C) − P(A ∩ B) − P(A ∩ C) − P(B ∩ C) + P(A ∩ B ∩ C)
Pelemparan koin bersisi angka dan gambar
Pelemparan satu buah koin
Sampel = {A, G}
\(\textbf{n(S)} = 2^1 = 2\)
P(muncul angka) = \(\frac{1}{2}\)
P(muncul gambar) = \(\frac{1}{2}\)
Pelemparan dua buah koin
| A | G | |
| A | (A, A) | (A, G) |
| G | (G, A) | (G, G) |
\(\textbf{S} = \lbrace \text{(A, A), (A, G), (G, A), (G, G)} \rbrace\)
\(\textbf{n(S)} = 2^2 = 4\)
Pada pelemparan dua koin:
- peluang muncul kedua sisi koin angka adalah \(\frac{1}{4}\)
- peluang muncul 1 angka dan 1 gambar adalah \(\frac{2}{4}\)
- peluang muncul kedua sisi koin gambar adalah \(\frac{1}{4}\)
Pelemparan tiga buah koin
| (A, A) | (A, G) | (G, A) | (G, G) | |
| A | (A, A, A) | (A, A, G) | (A, G, A) | (A, G, G) |
| G | (G, A, A) | (G, A, G) | (G, G, A) | (G, G, G) |
\(\textbf{S}\) = {(A, A, A), (A, A, G), (A, G, A), (A, G, G), (G, A, A), (G, A, G), (G, G, A), (G, G, G)}
\(\textbf{n(S)} = 2^3 = 8\)
Untuk pelemparan \(n\) buah koin bersisi angka dan gambar maka \(\textbf{n(S)} = 2^n\)
Pelemparan dadu bermata 1 s.d. 6
Pelemparan koin bersisi angka dan gambar
Pelemparan satu buah dadu
Sampel = {1, 2, 3, 4, 5, 6}
\(\textbf{n(S)} = 6^1 = 6\)
A = angka ganjil = {1, 3, 5}
n(A) = 3
P(muncul angka ganjil) = \(\textbf{P(A)} = \dfrac{\text{n(A)}}{\text{n(S)}} = \dfrac{3}{6}\)
B = angka genap = {2, 4, 6}
n(B) = 3
P(muncul angka genap) = \(\textbf{P(B)} = \dfrac{\text{n(B)}}{\text{n(S)}} = \dfrac{3}{6}\)
C = angka prima = {2, 3, 5}
n(C) = 3
P(muncul angka prima) = \(\textbf{P(C)} = \dfrac{\text{n(C)}}{\text{n(S)}} = \dfrac{3}{6}\)
D = angka komposit = {4, 6}
n(D) = 2
P(muncul angka komposit) = \(\textbf{P(D)} = \dfrac{\text{n(D)}}{\text{n(S)}} = \dfrac{2}{6}\)
E = faktor dari 6 = {1, 2, 3, 6}
n(E) = 4
P(muncul faktor dari 6) = \(\textbf{P(E)} = \dfrac{\text{n(E)}}{\text{n(S)}} = \dfrac{4}{6}\)
F = kelipatan 2 = {2, 4, 6}
n(F) = 3
P(muncul angka kelipatan 2) = \(\textbf{P(F)} = \dfrac{\text{n(F)}}{\text{n(S)}} = \dfrac{3}{6}\)
Pelemparan dua buah dadu
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | (1, 1) | (1, 2) | (1, 3) | (1, 4) | (1, 5) | (1, 6) |
| 2 | (2, 1) | (2, 2) | (2, 3) | (2, 4) | (2, 5) | (2, 6) |
| 3 | (3, 1) | (3, 2) | (3, 3) | (4, 4) | (3, 5) | (3, 6) |
| 4 | (4, 1) | (4, 2) | (4, 3) | (4, 4) | (4, 5) | (4, 6) |
| 5 | (5, 1) | (5, 2) | (5, 3) | (5, 4) | (5, 5) | (5, 6) |
| 6 | (6, 1) | (6, 2) | (6, 3) | (6, 4) | (6, 5) | (6, 6) |
Jumlah titik sampel \(\textbf{n(S)} = 6^2 = 36\)
Untuk pelemparan \(n\) buah dadu jumlah titik sampelnya \(\textbf{n(S)} = 6^n \)
A = kedua mata dadu angka sama = {(1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (6, 6)}
n(A) = 6
P(muncul kedua mata dadu angka sama) = \(\textbf{P(A)} = \dfrac{\text{n(A)}}{\text{n(S)}} = \dfrac{6}{36}\)
B = jumlah kedua mata dadu sama dengan 9 = {(3, 6), (6, 3), (4, 5), (5, 4)}
n(B) = 4
P(muncul kedua mata dadu angka sama) = \(\textbf{P(B)} = \dfrac{\text{n(B)}}{\text{n(S)}} = \dfrac{4}{36}\)
C = Selisih kedua mata dadu sama dengan 2 = {(1, 3), (3, 1), (2, 4), (4, 2), (3, 5), (5, 3), (4, 6), (6, 4)}
n(C) = 8
P(muncul kedua mata dadu angka sama) = \(\textbf{P(C)} = \dfrac{\text{n(C)}}{\text{n(S)}} = \dfrac{8}{36}\)
D = muncul kedua mata dadu angka prima = {(2, 2), (2, 3), (3, 2), (2, 5), (5, 2), (3, 5), (5, 3), (3, 3), (5, 5)}
n(D) = 9
P(muncul kedua mata dadu angka sama) = \(\textbf{P(D)} = \dfrac{\text{n(D)}}{\text{n(S)}} = \dfrac{9}{36}\)
Kartu Remi
♥ |
2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | J | Q | K | As |
♦ |
2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | J | Q | K | As |
♠ |
2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | J | Q | K | As |
♣ |
2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | J | Q | K | As |
Satu set kartu remi tanpa joker berisi 52 kartu yang terdiri dari:
- 13 kartu hati ♥
- 13 kartu wajik ♦
- 13 kartu sekop ♠
- 13 kartu keriting ♣
\(\textbf{n(S)} = 52\)
A = terambil kartu As { kartu As ♥, kartu As ♦, kartu As ♠, kartu As ♣}
n(A) = 4
P(terambil sebuah kartu As) = \(\textbf{P(A)} = \dfrac{\text{n(A)}}{\text{n(S)}} = \dfrac{4}{52}\)
B = terambil kartu yang berwarna hitam
Jumlah kartu yang berwarna hitam ada 26 (13 kartu sekop + 13 kartu keriting)
n(B) = 26
P(terambil sebuah kartu berwarna hitam) = \(\textbf{P(B)} = \dfrac{\text{n(B)}}{\text{n(S)}} = \dfrac{26}{52}\)
C = terambil kartu yang bergambar orang
Kartu yang bergambar orang adalah kartu J, Q, dan K. Karena ada 4 set maka total kartu bergambar orang ada \(4 \times 3 = 12\) buah.
n(C) = 12
P(terambil sebuah kartu bergambar orang) = \(\textbf{P(C)} = \dfrac{\text{n(C)}}{\text{n(S)}} = \dfrac{12}{52}\)
