Quiz-summary
0 of 30 questions completed
Pertanyaan:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
Information
Dear Students,
Welcome to today’s quiz! This is your opportunity to demonstrate what you’ve learned so far, so do your best. Please keep in mind that you have a maximum of 30 minutes to complete all the questions. Make sure to manage your time wisely and answer each question thoughtfully.
Good luck!
Anda telah menyelesaikan kuis sebelumnya. Oleh karena itu, Anda tidak dapat memulainya lagi.
Quiz is loading...
You must sign in or sign up to start the quiz.
You have to finish following quiz, to start this quiz:
Hasil
0 dari 30 pertanyaan terjawab dengan benar
Waktu Anda:
Time has elapsed
Anda telah meraih 0 dari 0 poin, (0)
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- Dijawab
- Ragu-Ragu
-
Pertanyaan 1 dari 30
1. Pertanyaan
1 points\(1\frac{4}{5}\pi\) radian = … °
Benar
\(1\frac{4}{5}\pi\) radian = \(\frac{9}{5}\pi \times \color{red} \frac{180^{\circ}}{\pi} \color{black} = 324^{\circ}\)
Salah
\(1\frac{4}{5}\pi\) radian = \(\frac{9}{5}\pi \times \color{red} \frac{180^{\circ}}{\pi} \color{black} = 324^{\circ}\)
-
Pertanyaan 2 dari 30
2. Pertanyaan
1 points\(216^{\circ} = \dotso \text{ radian}\)
Benar
\(216^{\circ} = 216^{\circ} \times \color{red} \frac{\pi}{180^{\circ}}\color{black} = 1\frac{1}{5}\pi\text{ rad }\)
Salah
\(216^{\circ} = 216^{\circ} \times \color{red} \frac{\pi}{180^{\circ}}\color{black} = 1\frac{1}{5}\pi\text{ rad }\)
-
Pertanyaan 3 dari 30
3. Pertanyaan
1 pointsPerhatikan segitiga siku-siku berikut:
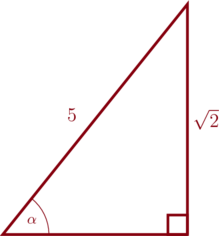
Nilai \(\cos \alpha \times \cot \alpha = \dotso\)
Benar
Mencari panjang sisi samping:
\(x^2 + (\sqrt{2})^2 = 5^2\)
\(x^2 + 2 = 25\)
\(x^2 = 25\:-\:2\)
\(x^2 = 23\)
\(x = \sqrt{23}\)
\(\cos \alpha \times \cot \alpha\)
\(\frac{\text{samping}}{\text{miring}}\times \frac{\text{samping}}{\text{depan}}\)
\(\frac{\sqrt{23}}{5}\times \frac{\sqrt{23}}{\sqrt{2}}\)
\(\frac{23}{5\sqrt{2}}\times \color{red}\frac{\sqrt{2}}{\sqrt{2}}\)
\(\frac{23}{10}\sqrt{2}\)
Salah
Mencari panjang sisi samping:
\(x^2 + (\sqrt{2})^2 = 5^2\)
\(x^2 + 2 = 25\)
\(x^2 = 25\:-\:2\)
\(x^2 = 23\)
\(x = \sqrt{23}\)
\(\cos \alpha \times \cot \alpha\)
\(\frac{\text{samping}}{\text{miring}}\times \frac{\text{samping}}{\text{depan}}\)
\(\frac{\sqrt{23}}{5}\times \frac{\sqrt{23}}{\sqrt{2}}\)
\(\frac{23}{5\sqrt{2}}\times \color{red}\frac{\sqrt{2}}{\sqrt{2}}\)
\(\frac{23}{10}\sqrt{2}\)
-
Pertanyaan 4 dari 30
4. Pertanyaan
1 pointsHasil dari \(\dfrac{\sin 60^{\circ}\cdot \cos 45^{\circ}\:-\:\cos 60^{\circ}\cdot \sin 45^{\circ}}{\tan 60^{\circ}} = \dotso\)
Benar
\(\dfrac{\frac{1}{2}\sqrt{3}\cdot \frac{1}{2}\sqrt{2}\:-\:\frac{1}{2}\cdot \frac{1}{2}\sqrt{2}}{\sqrt{3}} \)
\(\dfrac{\frac{1}{4}\sqrt{6}\:-\:\frac{1}{4}\sqrt{2}}{\sqrt{3}}\times \color{red}\dfrac{\sqrt{3}}{\sqrt{3}}\)
\(\dfrac{\frac{1}{4}\sqrt{18}\:-\:\frac{1}{4}\sqrt{6}}{3}\)
\(\frac{1}{12}\sqrt{18}\:-\:\frac{1}{12}\sqrt{6}\)
\(\frac{3}{12}\sqrt{2}\:-\:\frac{1}{12}\sqrt{6}\)
\(\frac{1}{4}\sqrt{2}\:-\:\frac{1}{12}\sqrt{6}\)
Salah
\(\dfrac{\frac{1}{2}\sqrt{3}\cdot \frac{1}{2}\sqrt{2}\:-\:\frac{1}{2}\cdot \frac{1}{2}\sqrt{2}}{\sqrt{3}} \)
\(\dfrac{\frac{1}{4}\sqrt{6}\:-\:\frac{1}{4}\sqrt{2}}{\sqrt{3}}\times \color{red}\dfrac{\sqrt{3}}{\sqrt{3}}\)
\(\dfrac{\frac{1}{4}\sqrt{18}\:-\:\frac{1}{4}\sqrt{6}}{3}\)
\(\frac{1}{12}\sqrt{18}\:-\:\frac{1}{12}\sqrt{6}\)
\(\frac{3}{12}\sqrt{2}\:-\:\frac{1}{12}\sqrt{6}\)
\(\frac{1}{4}\sqrt{2}\:-\:\frac{1}{12}\sqrt{6}\)
-
Pertanyaan 5 dari 30
5. Pertanyaan
1 pointsHasil dari \(\csc 30^{\circ}\cdot \sec 45^{\circ} + \cos 90^{\circ}\cdot \tan 19^{\circ} = \dotso\)
Benar
\(\csc 30^{\circ}\cdot \sec 45^{\circ} + \cos 90^{\circ}\cdot \tan 19^{\circ}\)
\(2\cdot \sqrt{2} + 0\)
\(2\sqrt{2}\)
Salah
\(\csc 30^{\circ}\cdot \sec 45^{\circ} + \cos 90^{\circ}\cdot \tan 19^{\circ}\)
\(2\cdot \sqrt{2} + 0\)
\(2\sqrt{2}\)
-
Pertanyaan 6 dari 30
6. Pertanyaan
1 points\(1\frac{1}{2}\pi \text{ radian} = \dotso ^{\circ}\)
Benar
\(1\frac{1}{2}\pi \text{ radian} = \frac{3}{2}\pi \times \frac{180^{\circ}}{\pi}\)
\(1\frac{1}{2}\pi \text{ radian} = 270^{\circ}\)
Salah
\(1\frac{1}{2}\pi \text{ radian} = \frac{3}{2}\pi \times \frac{180^{\circ}}{\pi}\)
\(1\frac{1}{2}\pi \text{ radian} = 270^{\circ}\)
-
Pertanyaan 7 dari 30
7. Pertanyaan
1 points\(1\text{ radian} = \dotso ^{\circ}\)
Benar
\(1\text{ radian} = \frac{180 ^{\circ}}{\pi}\)
\(1\text{ radian} = \frac{180 ^{\circ}}{\frac{22}{7}} = 57,27^{\circ}\)
Salah
\(1\text{ radian} = \frac{180 ^{\circ}}{\pi}\)
\(1\text{ radian} = \frac{180 ^{\circ}}{\frac{22}{7}} = 57,27^{\circ}\)
-
Pertanyaan 8 dari 30
8. Pertanyaan
1 points\(1^{\circ} = \dotso \text{ radian}\)
Benar
\(1^{\circ} = \frac{\pi}{180^{\circ}} \text{ radian}\)
Salah
\(1^{\circ} = \frac{\pi}{180^{\circ}} \text{ radian}\)
-
Pertanyaan 9 dari 30
9. Pertanyaan
1 points\(150^{\circ} = \dotso \text{ radian}\)
Benar
\(150^{\circ} = 150^{\circ}\times \frac{\pi}{180^{\circ}} \text{ radian}\)
\(150^{\circ} = \frac{5}{6}\pi\text{ radian}\)
Salah
\(150^{\circ} = 150^{\circ}\times \frac{\pi}{180^{\circ}} \text{ radian}\)
\(150^{\circ} = \frac{5}{6}\pi\text{ radian}\)
-
Pertanyaan 10 dari 30
10. Pertanyaan
1 pointsPerhatikan segitiga siku-siku berikut:
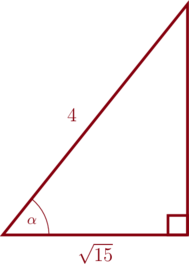
Nilai \(\sin \alpha + \csc \alpha = \dotso\)
Benar
Menentukan panjang sisi depan,
\(x^2 + (\sqrt{15})^2 = 4^2\)
\(x^2 + 15 = 16\)
\(x^2 = 1\)
\(x = 1\)
\(\sin \alpha + \csc \alpha\)
\(\frac{1}{4} + \frac{4}{1} = 4\frac{1}{4}\)
Salah
Menentukan panjang sisi depan,
\(x^2 + (\sqrt{15})^2 = 4^2\)
\(x^2 + 15 = 16\)
\(x^2 = 1\)
\(x = 1\)
\(\sin \alpha + \csc \alpha\)
\(\frac{1}{4} + \frac{4}{1} = 4\frac{1}{4}\)
-
Pertanyaan 11 dari 30
11. Pertanyaan
1 pointsPerhatikan segitiga siku-siku berikut:
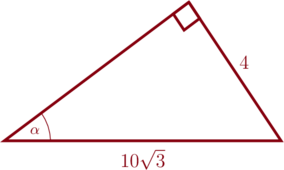
Jika \(\csc \alpha = \dfrac{\sqrt{3}}{5}\), maka nilai \(x\) adalah …
Benar
\(\csc \alpha = \dfrac{\sqrt{3}}{5}\)
\(\sin\alpha = \dfrac{5}{\sqrt{3}}\)
\(\dfrac{x}{10\sqrt{3}} = \dfrac{5}{\sqrt{3}}\)
\(x = \dfrac{5}{\cancel{\sqrt{3}}}\times 10\cancel{\sqrt{3}}\)
\(x = 50\)
Salah
\(\csc \alpha = \dfrac{\sqrt{3}}{5}\)
\(\sin\alpha = \dfrac{5}{\sqrt{3}}\)
\(\dfrac{x}{10\sqrt{3}} = \dfrac{5}{\sqrt{3}}\)
\(x = \dfrac{5}{\cancel{\sqrt{3}}}\times 10\cancel{\sqrt{3}}\)
\(x = 50\)
-
Pertanyaan 12 dari 30
12. Pertanyaan
1 pointsPerhatikan segitiga siku-siku berikut!
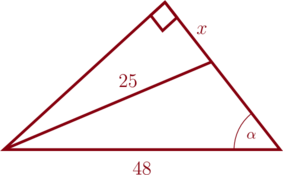
Jika \(\alpha = 30^{\circ}\), maka nilai \(x = \dotso\)
Benar
Perhatikan segitiga siku-siku yang besar,

\(\sin 30^{\circ} = \dfrac{y}{48}\)
\(\dfrac{1}{2} = \dfrac{y}{48}\)
\(y = 24\)
Lihat segitiga kecil dan tentukan nilai \(x\) menggunakan rumus pythagoras,
\(x^2 + 24^2 = 25^2\)
\(x^2 + 576 = 625\)
\(x^2 = 49\)
\(x = 7\)
Salah
Perhatikan segitiga siku-siku yang besar,

\(\sin 30^{\circ} = \dfrac{y}{48}\)
\(\dfrac{1}{2} = \dfrac{y}{48}\)
\(y = 24\)
Lihat segitiga kecil dan tentukan nilai \(x\) menggunakan rumus pythagoras,
\(x^2 + 24^2 = 25^2\)
\(x^2 + 576 = 625\)
\(x^2 = 49\)
\(x = 7\)
-
Pertanyaan 13 dari 30
13. Pertanyaan
1 pointsPerhatikan gabungan segitiga siku-siku berikut!
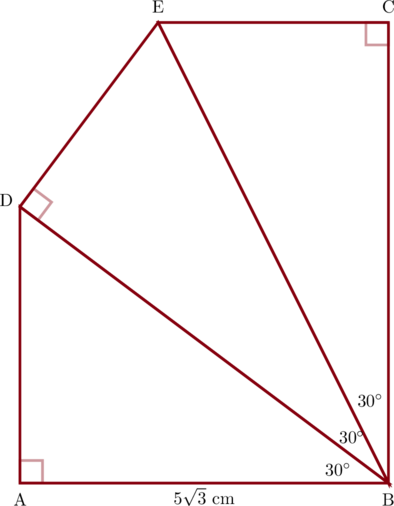
Jika panjang AB = \(5\sqrt{3}\) cm, maka panjang EC = … cm
Benar
Lihat ΔDAB,
\(\cos 30^{\circ} = \dfrac{\text{AB}}{\text{BD}}\)
\(\dfrac{\sqrt{3}{2}} = \dfrac{5\sqrt{3}}{\text{BD}}\)
\(\dfrac{\cancel{\sqrt{3}}}{2} = \dfrac{5\cancel{\sqrt{3}}}{\text{BD}}\)
\(\text{BD} = 10\)
Lihat ΔBDE,
\(\cos 30^{\circ} = \dfrac{\text{BD}}{\text{BE}}\)
\(\dfrac{\sqrt{3}}{2} = \dfrac{10}{\text{BE}}\)
\(\sqrt{3}\text{BE} = 20\)
\(\text{BE} = \dfrac{20}{\sqrt{3}}\)
Lihat ΔBCE,
\(\sin 30^{\circ} = \dfrac{\text{EC}}{\text{BE}}\)
\(\dfrac{1}{2} = \dfrac{\text{EC}}{\dfrac{20}{\sqrt{3}}}\)
\(\text{EC} = \dfrac{10}{\sqrt{3}}\)
\(\text{EC} = \dfrac{10}{3}\sqrt{3}\)
Salah
Lihat ΔDAB,
\(\cos 30^{\circ} = \dfrac{\text{AB}}{\text{BD}}\)
\(\dfrac{\sqrt{3}{2}} = \dfrac{5\sqrt{3}}{\text{BD}}\)
\(\dfrac{\cancel{\sqrt{3}}}{2} = \dfrac{5\cancel{\sqrt{3}}}{\text{BD}}\)
\(\text{BD} = 10\)
Lihat ΔBDE,
\(\cos 30^{\circ} = \dfrac{\text{BD}}{\text{BE}}\)
\(\dfrac{\sqrt{3}}{2} = \dfrac{10}{\text{BE}}\)
\(\sqrt{3}\text{BE} = 20\)
\(\text{BE} = \dfrac{20}{\sqrt{3}}\)
Lihat ΔBCE,
\(\sin 30^{\circ} = \dfrac{\text{EC}}{\text{BE}}\)
\(\dfrac{1}{2} = \dfrac{\text{EC}}{\dfrac{20}{\sqrt{3}}}\)
\(\text{EC} = \dfrac{10}{\sqrt{3}}\)
\(\text{EC} = \dfrac{10}{3}\sqrt{3}\)
-
Pertanyaan 14 dari 30
14. Pertanyaan
1 pointsHasil dari \(\dfrac{\sin 30^{\circ}\cdot \cos 60^{\circ} + \cos 30^{\circ}\cdot \sin 60^{\circ}}{\tan 45^{\circ}} = \dotso\)
Benar
\(\dfrac{\frac{1}{2}\cdot \frac{1}{2} + \frac{1}{2}\sqrt{3}\cdot \frac{1}{2}\sqrt{3}}{1}\)
\(\frac{1}{4} + \frac{3}{4} = 1\)
Salah
\(\dfrac{\frac{1}{2}\cdot \frac{1}{2} + \frac{1}{2}\sqrt{3}\cdot \frac{1}{2}\sqrt{3}}{1}\)
\(\frac{1}{4} + \frac{3}{4} = 1\)
-
Pertanyaan 15 dari 30
15. Pertanyaan
1 pointsHasil dari \(\dfrac{\csc 30^{\circ}\cdot \sec 60^{\circ} + \cot 30^{\circ}}{\sin 90^{\circ} + \cos 0^{\circ}} = \dotso\)
Benar
\(\dfrac{2\cdot 2 + \sqrt{3}}{1 + 1}\)
\(\dfrac{4 + \sqrt{3}}{2}\)
\(2 + \dfrac{1}{2}\sqrt{3}\)
Salah
\(\dfrac{2\cdot 2 + \sqrt{3}}{1 + 1}\)
\(\dfrac{4 + \sqrt{3}}{2}\)
\(2 + \dfrac{1}{2}\sqrt{3}\)
-
Pertanyaan 16 dari 30
16. Pertanyaan
1 pointsHasil dari \(\dfrac{\tan \frac{1}{4}\pi + \cos \frac{1}{2}\pi \cdot \sin \frac{1}{3}\pi}{\csc \frac{1}{4}\pi} = \dotso\)
Benar
\(\dfrac{\tan 45^{\circ} + \cos 90^{\circ} \cdot \sin 60^{\circ}}{\csc 45^{\circ}}\)
\(\dfrac{1 + 0\cdot \frac{1}{2}\sqrt{3}}{\sqrt{2}}\)
\(\dfrac{1}{\sqrt{2}}\times \color{red} \dfrac{\sqrt{2}}{\sqrt{2}}\)
\(\dfrac{1}{2}\sqrt{2}\)
Salah
\(\dfrac{\tan 45^{\circ} + \cos 90^{\circ} \cdot \sin 60^{\circ}}{\csc 45^{\circ}}\)
\(\dfrac{1 + 0\cdot \frac{1}{2}\sqrt{3}}{\sqrt{2}}\)
\(\dfrac{1}{\sqrt{2}}\times \color{red} \dfrac{\sqrt{2}}{\sqrt{2}}\)
\(\dfrac{1}{2}\sqrt{2}\)
-
Pertanyaan 17 dari 30
17. Pertanyaan
1 pointsHasil dari \(\sin^2 30^{\circ} + \cos^2 30^{\circ}\) adalah …
Benar
\((\frac{1}{2})^2 + (\frac{1}{2}\sqrt{3})^2\)
\(\frac{1}{4} + \frac{3}{4} = 1\)
Salah
\((\frac{1}{2})^2 + (\frac{1}{2}\sqrt{3})^2\)
\(\frac{1}{4} + \frac{3}{4} = 1\)
-
Pertanyaan 18 dari 30
18. Pertanyaan
1 pointsKoordinat polar dari titik \((2, 2\sqrt{3})\) adalah …
Benar
Koordinat polar = \((r, \theta)\)
\(r = \sqrt{x^2 + y^2}\)
\(r = \sqrt{2^2 + (2\sqrt{3})^2}\)
\(r = \sqrt{4 + 12}\)
\(r = \sqrt{16} = 4\)
\(\tan \theta = \frac{y}{x}\)
\(\tan \theta = \frac{2\sqrt{3}}{2} = \sqrt{3}\)
\(\theta = 60^{\circ}\)
Titik \((2, 2\sqrt{3})\) berada di kuadran I
Jadi kordinat polarnya adalah \((4, 60^{\circ})\)
Salah
Koordinat polar = \((r, \theta)\)
\(r = \sqrt{x^2 + y^2}\)
\(r = \sqrt{2^2 + (2\sqrt{3})^2}\)
\(r = \sqrt{4 + 12}\)
\(r = \sqrt{16} = 4\)
\(\tan \theta = \frac{y}{x}\)
\(\tan \theta = \frac{2\sqrt{3}}{2} = \sqrt{3}\)
\(\theta = 60^{\circ}\)
Titik \((2, 2\sqrt{3})\) berada di kuadran I
Jadi kordinat polarnya adalah \((4, 60^{\circ})\)
-
Pertanyaan 19 dari 30
19. Pertanyaan
1 pointsKoordinat kartesius dari titik \((2\sqrt{3}, 60^{\circ})\) adalah …
Benar
\(x = r\cdot \cos \theta\)
\(x = 2\sqrt{3}\cdot \cos 60^{\circ}\)
\(x = 2\sqrt{3}\cdot \frac{1}{2} = \sqrt{3}\)
\(y = r\cdot \sin \theta\)
\(x = 2\sqrt{3}\cdot \sin 60^{\circ}\)
\(x = 2\sqrt{3}\cdot \frac{1}{2}\sqrt{3} = 3\)
Jadi koordinat kartesiusnya adalah \((\sqrt{3}, 3)\)
Salah
\(x = r\cdot \cos \theta\)
\(x = 2\sqrt{3}\cdot \cos 60^{\circ}\)
\(x = 2\sqrt{3}\cdot \frac{1}{2} = \sqrt{3}\)
\(y = r\cdot \sin \theta\)
\(x = 2\sqrt{3}\cdot \sin 60^{\circ}\)
\(x = 2\sqrt{3}\cdot \frac{1}{2}\sqrt{3} = 3\)
Jadi koordinat kartesiusnya adalah \((\sqrt{3}, 3)\)
-
Pertanyaan 20 dari 30
20. Pertanyaan
1 pointsDiketahui koordinat polar dari titik \((x, 5)\) adalah \((r, 30^{\circ})\). Nilai \(x\) yang mungkin adalah …
Benar
\(y = r\cdot \sin \theta\)
\(5 = r\cdot \sin 30^{\circ}\)
\(5 = r\cdot \frac{1}{2}\)
\(r = 10\)
\(x = r\cdot \cos \theta\)
\(x = 10\cdot \cos 30^{\circ}\)
\(x = 10\cdot \frac{1}{2}\sqrt{3}\)
\(x = 5\sqrt{3}\)
Salah
\(y = r\cdot \sin \theta\)
\(5 = r\cdot \sin 30^{\circ}\)
\(5 = r\cdot \frac{1}{2}\)
\(r = 10\)
\(x = r\cdot \cos \theta\)
\(x = 10\cdot \cos 30^{\circ}\)
\(x = 10\cdot \frac{1}{2}\sqrt{3}\)
\(x = 5\sqrt{3}\)
-
Pertanyaan 21 dari 30
21. Pertanyaan
1 pointsTitik P\((6, y)\) terletak di kuadran I, sudut yang dibentuk oleh sumbu x positif, titik asal (0, 0), dan titik P adalah \(\alpha\). Jika \(\sin \alpha = \frac{6}{10}\), maka nilai \(y\) adalah …
Benar
Menentukan sisi miring segitiga,
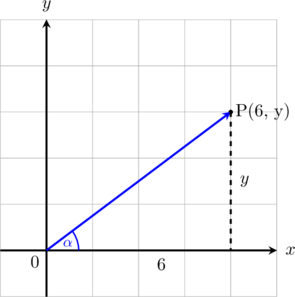
Panjang sisi miring = \(\sqrt{6^2 + y^2}\)
Panjang sisi miring = \(\sqrt{36 + y^2}\)
\(\sin \alpha = \dfrac{6}{10}\)
\(\dfrac{y}{\sqrt{36 + y^2}} = \dfrac{3}{5}\)
Kuadratkan kedua ruas,
\(\dfrac{y^2}{36 + y^2} = \dfrac{9}{25}\)
\(25y^2 = 9(36 + y^2)\)
\(25y^2 = 324 + 9y^2\)
\(25y^2\:-\:9y^2 = 324\)
\(16y^2 = 324\)
\(y^2 = \dfrac{324}{16}\)
\(y = \sqrt{\dfrac{324}{16}}\)
\(y = \dfrac{18}{4} = 4,5\)
Salah
Menentukan sisi miring segitiga,

Panjang sisi miring = \(\sqrt{6^2 + y^2}\)
Panjang sisi miring = \(\sqrt{36 + y^2}\)
\(\sin \alpha = \dfrac{6}{10}\)
\(\dfrac{y}{\sqrt{36 + y^2}} = \dfrac{3}{5}\)
Kuadratkan kedua ruas,
\(\dfrac{y^2}{36 + y^2} = \dfrac{9}{25}\)
\(25y^2 = 9(36 + y^2)\)
\(25y^2 = 324 + 9y^2\)
\(25y^2\:-\:9y^2 = 324\)
\(16y^2 = 324\)
\(y^2 = \dfrac{324}{16}\)
\(y = \sqrt{\dfrac{324}{16}}\)
\(y = \dfrac{18}{4} = 4,5\)
-
Pertanyaan 22 dari 30
22. Pertanyaan
1 pointsTono mengamati puncak gedung dengan sudut elevasi \(30^{\circ}\). Jika Tono bergerak maju mendekati gedung sejauh 10 m, maka Tono akan melihat puncak gedung dengan sudut elevasi \(45^{\circ}\). Jika dianggap tinggi mata Tono 150 cm, maka tinggi gedung tersebut diukur dari permukaan tanah adalah …
Benar
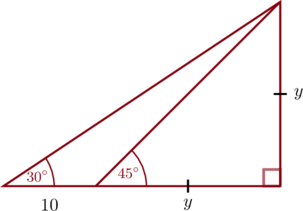
\(\tan 30^{\circ} = \dfrac{y}{10 + y}\)
\(\dfrac{1}{\sqrt{3}}= \dfrac{y}{10 + y}\)
\(10 + y = \sqrt{3}y\)
\(10 = \sqrt{3}y\:-\:y\)
\(10 = y(\sqrt{3}\:-\:1)\)
\(y = \dfrac{10}{\sqrt{3}\:-\:1}\times \color{red} \dfrac{\sqrt{3} + 1}{\sqrt{3} + 1}\)
\(y = \dfrac{10\sqrt{3} + 10}{3\:-\:1}\)
\(y = \dfrac{10\sqrt{3} + 10}{2}\)
\(y = 5\sqrt{3} + 5 \text{ m}\)
Ketinggian gedung = \(y\) + tinggi mata Tono
Ketinggian gedung = \(5\sqrt{3} + 5 + 1,5 \text{ m}\)
Ketinggian gedung = \(6,5 + 5\sqrt{3}\text{ m}\)
Salah

\(\tan 30^{\circ} = \dfrac{y}{10 + y}\)
\(\dfrac{1}{\sqrt{3}}= \dfrac{y}{10 + y}\)
\(10 + y = \sqrt{3}y\)
\(10 = \sqrt{3}y\:-\:y\)
\(10 = y(\sqrt{3}\:-\:1)\)
\(y = \dfrac{10}{\sqrt{3}\:-\:1}\times \color{red} \dfrac{\sqrt{3} + 1}{\sqrt{3} + 1}\)
\(y = \dfrac{10\sqrt{3} + 10}{3\:-\:1}\)
\(y = \dfrac{10\sqrt{3} + 10}{2}\)
\(y = 5\sqrt{3} + 5 \text{ m}\)
Ketinggian gedung = \(y\) + tinggi mata Tono
Ketinggian gedung = \(5\sqrt{3} + 5 + 1,5 \text{ m}\)
Ketinggian gedung = \(6,5 + 5\sqrt{3}\text{ m}\)
-
Pertanyaan 23 dari 30
23. Pertanyaan
1 pointsPernyataan di bawah ini yang salah adalah …
Benar
Salah
-
Pertanyaan 24 dari 30
24. Pertanyaan
1 pointsPernyataan di bawah ini yang benar adalah …
Benar
Salah
-
Pertanyaan 25 dari 30
25. Pertanyaan
1 pointsDiketahui \(\sin \alpha = 0,8\) dan \(\cos \beta = \frac{1}{3}\), dengan \(\alpha\) dan \(\beta\) sudut lancip. Nilai \(\tan \alpha \times \csc \beta\) adalah …
Benar
\(\sin \alpha = 0,8 = \frac{8}{10}\)
\(\tan \alpha = \frac{8}{6} = \frac{4}{3}\)
\(\cos \beta = \frac{1}{3}\)
\(\csc \beta = \frac{3}{2\sqrt{2}} = \frac{3\sqrt{2}}{4}\)
\(\tan \alpha \times \csc \beta\)
\(\frac{4}{3} \times \frac{3\sqrt{2}}{4}\)
\(\sqrt{2}\)
Salah
\(\sin \alpha = 0,8 = \frac{8}{10}\)
\(\tan \alpha = \frac{8}{6} = \frac{4}{3}\)
\(\cos \beta = \frac{1}{3}\)
\(\csc \beta = \frac{3}{2\sqrt{2}} = \frac{3\sqrt{2}}{4}\)
\(\tan \alpha \times \csc \beta\)
\(\frac{4}{3} \times \frac{3\sqrt{2}}{4}\)
\(\sqrt{2}\)
-
Pertanyaan 26 dari 30
26. Pertanyaan
1 points\(\dfrac{1 + \cos 30^{\circ} + \cos 60^{\circ}}{\sin 60^{\circ} + \sin 30^{\circ}} = \dotso\)
Benar
\(\dfrac{1 + \frac{1}{2}\sqrt{3} + \frac{1}{2}}{\frac{1}{2}\sqrt{3} + \frac{1}{2}}\)
\(\dfrac{\frac{\sqrt{3} + 3}{2}}{\frac{\sqrt{3} + 1}{2}}\)
\(\dfrac{\sqrt{3} + 3}{\sqrt{3} + 1}\times \color{red} \dfrac{\sqrt{3} \:-\:1}{\sqrt{3} \:-\:1}\)
\(\dfrac{3\:-\:\sqrt{3} + 3\sqrt{3} \:-\:1}{3\:-\:1}\)
\(\dfrac{2\sqrt{3}}{2}\)
\(\sqrt{3} = \cot 30^{\circ}\)
Salah
\(\dfrac{1 + \frac{1}{2}\sqrt{3} + \frac{1}{2}}{\frac{1}{2}\sqrt{3} + \frac{1}{2}}\)
\(\dfrac{\frac{\sqrt{3} + 3}{2}}{\frac{\sqrt{3} + 1}{2}}\)
\(\dfrac{\sqrt{3} + 3}{\sqrt{3} + 1}\times \color{red} \dfrac{\sqrt{3} \:-\:1}{\sqrt{3} \:-\:1}\)
\(\dfrac{3\:-\:\sqrt{3} + 3\sqrt{3} \:-\:1}{3\:-\:1}\)
\(\dfrac{2\sqrt{3}}{2}\)
\(\sqrt{3} = \cot 30^{\circ}\)
-
Pertanyaan 27 dari 30
27. Pertanyaan
1 pointsJika \(4\sin x \:-\:2\sqrt{2} = 0\), dengan \(x\) adalah sudut lancip, maka nilai \(\tan x = \dotso\)
Benar
\(4\sin x \:-\:2\sqrt{2} = 0\)
\(4\sin x = 2\sqrt{2}\)
\(\sin x = \frac{1}{2}\sqrt{2}\)
\(x = 45^{\circ}\)
Jadi,
\(\tan 45^{\circ} = 1\)
Salah
\(4\sin x \:-\:2\sqrt{2} = 0\)
\(4\sin x = 2\sqrt{2}\)
\(\sin x = \frac{1}{2}\sqrt{2}\)
\(x = 45^{\circ}\)
Jadi,
\(\tan 45^{\circ} = 1\)
-
Pertanyaan 28 dari 30
28. Pertanyaan
1 pointsPerhatikan gambar berikut:

Nilai \(\sin \alpha = \dotso\)
Benar
Panjang sisi miring = \(\sqrt{15^2 + 8^2}\)
Panjang sisi miring = \(\sqrt{225 + 64}\)
Panjang sisi miring = \(\sqrt{289} = 17\)
\(\sin \alpha = \dfrac{\text{depan}}{\text{miring}}\)
\(\sin \alpha = -\dfrac{8}{17}\)
Di kuadran IV nilai \(\sin \alpha\) negatif
Salah
Panjang sisi miring = \(\sqrt{15^2 + 8^2}\)
Panjang sisi miring = \(\sqrt{225 + 64}\)
Panjang sisi miring = \(\sqrt{289} = 17\)
\(\sin \alpha = \dfrac{\text{depan}}{\text{miring}}\)
\(\sin \alpha = -\dfrac{8}{17}\)
Di kuadran IV nilai \(\sin \alpha\) negatif
-
Pertanyaan 29 dari 30
29. Pertanyaan
1 pointsPerhatikan gambar berikut:
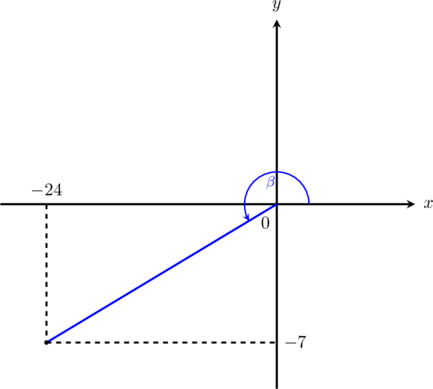
Nilai \(\cot \beta = \dotso\)
Benar
\(\cot \beta = \dfrac{\text{samping}}{\text{depan}}\)
\(\cot \beta = \dfrac{24}{7}\)
Di kuadran III nilai \(\cot \beta\) positif
Salah
\(\cot \beta = \dfrac{\text{samping}}{\text{depan}}\)
\(\cot \beta = \dfrac{24}{7}\)
Di kuadran III nilai \(\cot \beta\) positif
-
Pertanyaan 30 dari 30
30. Pertanyaan
1 pointsPerhatikan gambar berikut:

Nilai \(\cos \gamma = \dotso\)
Benar
Panjang sisi miring = \(\sqrt{6^2 + 8^2}\)
Panjang sisi miring = \(\sqrt{36 + 64}\)
Panjang sisi miring = \(\sqrt{100} = 10\)
\(\cos \gamma = \dfrac{\text{samping}}{\text{miring}}\)
\(\cos \gamma = -\dfrac{8}{10}\)
\(\cos \gamma = -0,8\)
Di kuadran II \(\cos \gamma\) bernilai negatif
Salah
Panjang sisi miring = \(\sqrt{6^2 + 8^2}\)
Panjang sisi miring = \(\sqrt{36 + 64}\)
Panjang sisi miring = \(\sqrt{100} = 10\)
\(\cos \gamma = \dfrac{\text{samping}}{\text{miring}}\)
\(\cos \gamma = -\dfrac{8}{10}\)
\(\cos \gamma = -0,8\)
Di kuadran II \(\cos \gamma\) bernilai negatif
