Quiz-summary
0 of 20 questions completed
Pertanyaan:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
Information
Dear Students,
Welcome to today’s quiz! This is your opportunity to demonstrate what you’ve learned so far, so do your best. Please keep in mind that you have a maximum of 30 minutes to complete all the questions. Make sure to manage your time wisely and answer each question thoughtfully.
Good luck!
Anda telah menyelesaikan kuis sebelumnya. Oleh karena itu, Anda tidak dapat memulainya lagi.
Quiz is loading...
You must sign in or sign up to start the quiz.
You have to finish following quiz, to start this quiz:
Hasil
0 dari 20 pertanyaan terjawab dengan benar
Waktu Anda:
Time has elapsed
Anda telah meraih 0 dari 0 poin, (0)
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- Dijawab
- Ragu-Ragu
-
Pertanyaan 1 dari 20
1. Pertanyaan
1 pointsPerhatikan gambar di bawah ini:
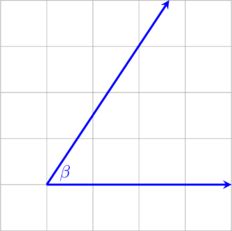
Jika panjang 1 kotak adalah 1 satuan, maka \(\sin \beta = \dotso\)Benar
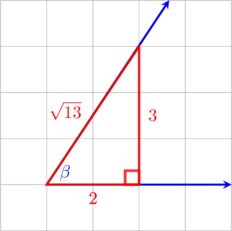
\(\sin \beta = \dfrac{\text{depan}}{\text{miring}}\)
\(\sin \beta = \dfrac{3}{\sqrt{13}}\)
\(\sin \beta = \dfrac{3}{13}\sqrt{13}\)
Salah

\(\sin \beta = \dfrac{\text{depan}}{\text{miring}}\)
\(\sin \beta = \dfrac{3}{\sqrt{13}}\)
\(\sin \beta = \dfrac{3}{13}\sqrt{13}\)
-
Pertanyaan 2 dari 20
2. Pertanyaan
1 pointsJika titik A\((m, n)\), O\((0, 0)\), OA = \(r\) dan OA dengan sumbu \(x\) positif membentuk sudut \(\alpha\), maka \(\cos \alpha = \dotso\)
Benar
\(\cos \alpha = \dfrac{\text{samping}}{\text{miring}}\)
\(\cos \alpha = \dfrac{m}{r}\)
Salah
\(\cos \alpha = \dfrac{\text{samping}}{\text{miring}}\)
\(\cos \alpha = \dfrac{m}{r}\)
-
Pertanyaan 3 dari 20
3. Pertanyaan
1 pointsUntuk sudut α dan β pada gambar di bawah ini, maka pernyataan berikut yang benar adalah …
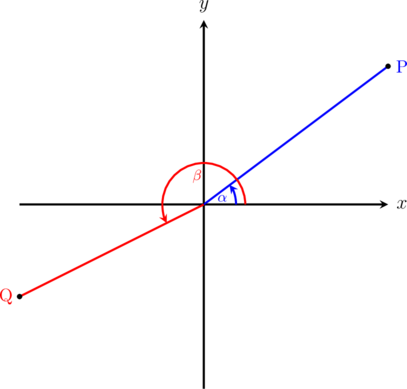 Benar
Benar
Semua fungsi trigonometri di kuadran I bernilai positif.
Tangen di kuadran III bernilai positif.
Salah
Semua fungsi trigonometri di kuadran I bernilai positif.
Tangen di kuadran III bernilai positif.
-
Pertanyaan 4 dari 20
4. Pertanyaan
1 points\(1\dfrac{3}{4}\pi \text{ rad} + 3\dfrac{1}{5}\pi \text{ rad} = \dotso ^{\circ}\)
Benar
\(1\dfrac{3}{4}\pi \text{ rad} + 3\dfrac{1}{5}\pi \text{ rad}\)
\(\dfrac{7}{4}\pi\times \dfrac{180^{\circ}}{\pi} + \dfrac{16}{5}\pi\times \dfrac{180^{\circ}}{\pi}\)
\(315^{\circ} + 576^{\circ}\)
\(891^{\circ}\)
Salah
\(1\dfrac{3}{4}\pi \text{ rad} + 3\dfrac{1}{5}\pi \text{ rad}\)
\(\dfrac{7}{4}\pi\times \dfrac{180^{\circ}}{\pi} + \dfrac{16}{5}\pi\times \dfrac{180^{\circ}}{\pi}\)
\(315^{\circ} + 576^{\circ}\)
\(891^{\circ}\)
-
Pertanyaan 5 dari 20
5. Pertanyaan
1 pointsSebuah eskalator memiliki panjang 34 meter dan tinggi 17 meter menghubungkan lantai dasar dengan lantai 1 di sebuah stasiun kereta api. Jika β adalah sudut yang dibentuk antara eskalator dengan lantai dasar, maka nilai β adalah …
Benar
\(\sin \beta = \dfrac{\text{depan}}{\text{miring}}\)
\(\sin \beta = \dfrac{17}{34} = \dfrac{1}{2}\)
\(\beta = 30^{\circ}\)
Salah
\(\sin \beta = \dfrac{\text{depan}}{\text{miring}}\)
\(\sin \beta = \dfrac{17}{34} = \dfrac{1}{2}\)
\(\beta = 30^{\circ}\)
-
Pertanyaan 6 dari 20
6. Pertanyaan
1 pointsJika \(\csc \beta = \dfrac{37}{35}\) maka nilai \(\tan \beta = \dotso\)
Benar
\(\csc \beta = \dfrac{37}{35} = \dfrac{\text{miring}}{\text{depan}}\)
\(\tan \beta = \dfrac{\text{depan}}{\text{samping}} = \dfrac{35}{12}\)
Salah
\(\csc \beta = \dfrac{37}{35} = \dfrac{\text{miring}}{\text{depan}}\)
\(\tan \beta = \dfrac{\text{depan}}{\text{samping}} = \dfrac{35}{12}\)
-
Pertanyaan 7 dari 20
7. Pertanyaan
1 pointsSeseorang melakukan perjalanan dengan rute A – B – C – D – E seperti pada gambar di bawah ini:

Jika \(y\) merupakan perbedaan ketinggian tempat antara A dan E, maka nilai \(y\) adalah …
(\(\sin 23^{\circ} = 0,4)\)
Benar
Perhatikan gambar berikut:

\(y = m + n\)
\(y = 2\sin 23^{\circ} + 5\sin 23^{\circ}\)
\(y = 2(0,4) + 5(0, 4)\)
\(y = 0,8 + 2\)
\(y = 2,8 \text{ km}\)Jadi perbedaan ketinggian antara tempat A dan E adalah 2,8 km
Salah
Perhatikan gambar berikut:

\(y = m + n\)
\(y = 2\sin 23^{\circ} + 5\sin 23^{\circ}\)
\(y = 2(0,4) + 5(0, 4)\)
\(y = 0,8 + 2\)
\(y = 2,8 \text{ km}\)Jadi perbedaan ketinggian antara tempat A dan E adalah 2,8 km
-
Pertanyaan 8 dari 20
8. Pertanyaan
1 points\(\dfrac{\cos 30^{\circ}\times \csc 60^{\circ}}{\tan 30^{\circ}} = \dotso\)
Benar
\(\dfrac{\frac{1}{2}\sqrt{3}\times \frac{2}{\sqrt{3}}}{\frac{1}{\sqrt{3}}} = \sqrt{3}\)
Salah
\(\dfrac{\frac{1}{2}\sqrt{3}\times \frac{2}{\sqrt{3}}}{\frac{1}{\sqrt{3}}} = \sqrt{3}\)
-
Pertanyaan 9 dari 20
9. Pertanyaan
1 pointsNilai dari \(\sin 45^{\circ}\cdot \cos 60^{\circ} + \cos 45^{\circ}\cdot \sin 60^{\circ} = \dotso\)
Benar
\(\sin 45^{\circ}\cdot \cos 60^{\circ} + \cos 45^{\circ}\cdot \sin 60^{\circ}\)
\(\frac{1}{2}\sqrt{2}\cdot \frac{1}{2} +\frac{1}{2}\sqrt{2}\cdot \frac{1}{2}\sqrt{3}\)
\(\frac{1}{4}\sqrt{2} +\frac{1}{4}\sqrt{6}\)
\(\dfrac{\sqrt{2} + \sqrt{6}}{4}\)
Salah
\(\sin 45^{\circ}\cdot \cos 60^{\circ} + \cos 45^{\circ}\cdot \sin 60^{\circ}\)
\(\frac{1}{2}\sqrt{2}\cdot \frac{1}{2} +\frac{1}{2}\sqrt{2}\cdot \frac{1}{2}\sqrt{3}\)
\(\frac{1}{4}\sqrt{2} +\frac{1}{4}\sqrt{6}\)
\(\dfrac{\sqrt{2} + \sqrt{6}}{4}\)
-
Pertanyaan 10 dari 20
10. Pertanyaan
1 pointsNilai dari \(\sec \frac{1}{4}\pi \cdot \cot \frac{1}{3}\pi + \sqrt{6}\cdot \csc \frac{1}{2}\pi = \dotso\)
Benar
\(\sec \frac{1}{4}\pi \cdot \cot \frac{1}{3}\pi + \sqrt{6}\cdot \csc \frac{1}{2}\pi\)
\(\sqrt{2}\cdot \frac{1}{3}\sqrt{3} + \sqrt{6}\cdot 1\)
\(\frac{1}{3}\sqrt{6} + \sqrt{6}\)
\(\frac{4}{3}\sqrt{6}\)
Salah
\(\sec \frac{1}{4}\pi \cdot \cot \frac{1}{3}\pi + \sqrt{6}\cdot \csc \frac{1}{2}\pi\)
\(\sqrt{2}\cdot \frac{1}{3}\sqrt{3} + \sqrt{6}\cdot 1\)
\(\frac{1}{3}\sqrt{6} + \sqrt{6}\)
\(\frac{4}{3}\sqrt{6}\)
-
Pertanyaan 11 dari 20
11. Pertanyaan
1 pointsJika titik P\((x, 14)\) adalah sebuah titik di kuadran II, O adalah titik (0, 0), dan β adalah sudut yang dibentuk oleh sumbu \(x\) positif dengan garis OP, serta \(\sin \beta = \dfrac{7}{25}\), maka nilai \(x\) adalah …
Benar
Panjang OP (sisi miring) = \(\sqrt{x^2 + 14^2}\)
\(\sin \beta = \dfrac{\text{depan}}{\text{miring}}\)
\(\dfrac{7}{25} = \dfrac{14}{\sqrt{x^2 + 196}}\)
\(\dfrac{\cancel{7}}{25} = \dfrac{\cancelto{2}{14}}{\sqrt{x^2 + 196}}\)
\(50 = \sqrt{x^2 + 196}\)
\(2500 = x^2 + 196\)
\(x^2 = 2500\:-\:196\)
\(x^2 = 2304\)
\(x = \pm\sqrt{2304}\)
\(x = \pm 48\)
Karena titik P berada di kuadran II, maka nilai \(x\) haruslah bertanda negatif, jadi \(x = -48\)
Salah
Panjang OP (sisi miring) = \(\sqrt{x^2 + 14^2}\)
\(\sin \beta = \dfrac{\text{depan}}{\text{miring}}\)
\(\dfrac{7}{25} = \dfrac{14}{\sqrt{x^2 + 196}}\)
\(\dfrac{\cancel{7}}{25} = \dfrac{\cancelto{2}{14}}{\sqrt{x^2 + 196}}\)
\(50 = \sqrt{x^2 + 196}\)
\(2500 = x^2 + 196\)
\(x^2 = 2500\:-\:196\)
\(x^2 = 2304\)
\(x = \pm\sqrt{2304}\)
\(x = \pm 48\)
Karena titik P berada di kuadran II, maka nilai \(x\) haruslah bertanda negatif, jadi \(x = -48\)
-
Pertanyaan 12 dari 20
12. Pertanyaan
1 pointsJika titik Q\((x, 5)\) adalah sebuah titik yang terletak di kuadran I, O adalah titik (0, 0), dan α adalah sudut yang dibentuk oleh garis OQ dengan sumbu \(x\) positif, serta \(\sin \alpha = \dfrac{15}{17}\), maka nilai \(x\) adalah …
Benar
Panjang OQ (sisi miring) = \(\sqrt{x^2 + 5^2}\)
\(\sin \alpha = \dfrac{\text{depan}}{\text{miring}}\)
\(\dfrac{\cancelto{3}{15}}{17} = \dfrac{\cancel{5}}{\sqrt{x^2 + 25}}\)
\(3\sqrt{x^2 + 25} = 17\)
Kuadratkan kedua ruas,
\(9(x^2 + 25) = 289\)
\(9x^2 + 225 = 289\)
\(9x^2 = 289\:-\:225\)
\(9x^2 = 64\)
\(x^2 = \dfrac{64}{9}\)
\(x = \pm \sqrt{\dfrac{64}{9}}\)
\(x = \pm \dfrac{8}{3}\)
Karena \(x\) terletak di kuadran I, maka nilai \(x = \dfrac{8}{3}\)
Salah
Panjang OQ (sisi miring) = \(\sqrt{x^2 + 5^2}\)
\(\sin \alpha = \dfrac{\text{depan}}{\text{miring}}\)
\(\dfrac{\cancelto{3}{15}}{17} = \dfrac{\cancel{5}}{\sqrt{x^2 + 25}}\)
\(3\sqrt{x^2 + 25} = 17\)
Kuadratkan kedua ruas,
\(9(x^2 + 25) = 289\)
\(9x^2 + 225 = 289\)
\(9x^2 = 289\:-\:225\)
\(9x^2 = 64\)
\(x^2 = \dfrac{64}{9}\)
\(x = \pm \sqrt{\dfrac{64}{9}}\)
\(x = \pm \dfrac{8}{3}\)
Karena \(x\) terletak di kuadran I, maka nilai \(x = \dfrac{8}{3}\)
-
Pertanyaan 13 dari 20
13. Pertanyaan
1 pointsPerhatikan gambar di bawah ini:
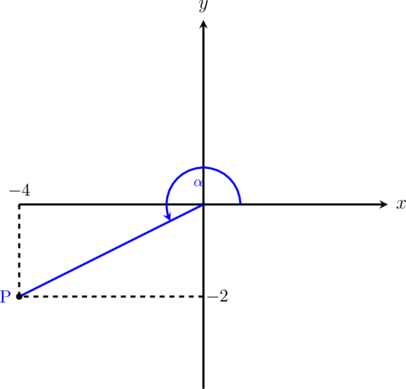
Nilai \(\csc \alpha = \dotso\)
Benar
Panjang OP (sisi miring) = \(\sqrt{4^2 + 2^2}\)
Panjang OP (sisi miring) = \(\sqrt{20} = 2\sqrt{5}\)
\(\csc \alpha = \dfrac{\text{miring}}{\text{depan}}\)
\(\csc \alpha = -\dfrac{2\sqrt{5}}{2}\)
\(\csc \alpha = -\sqrt{5}\)
\(\csc \alpha\) di kuadran III bernilai negatif
Salah
Panjang OP (sisi miring) = \(\sqrt{4^2 + 2^2}\)
Panjang OP (sisi miring) = \(\sqrt{20} = 2\sqrt{5}\)
\(\csc \alpha = \dfrac{\text{miring}}{\text{depan}}\)
\(\csc \alpha = -\dfrac{2\sqrt{5}}{2}\)
\(\csc \alpha = -\sqrt{5}\)
\(\csc \alpha\) di kuadran III bernilai negatif
-
Pertanyaan 14 dari 20
14. Pertanyaan
1 pointsPerhatikan gambar di bawah ini:
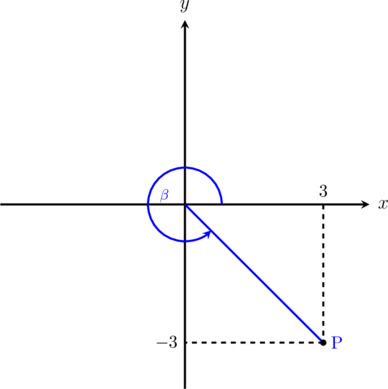
Nilai \(cot \beta = \dotso\)
Benar
\(\cot \beta = \dfrac{\text{samping}}{\text{depan}}\)
\(\cot \beta = -\dfrac{3}{3} = -1\)
Salah
\(\cot \beta = \dfrac{\text{samping}}{\text{depan}}\)
\(\cot \beta = -\dfrac{3}{3} = -1\)
-
Pertanyaan 15 dari 20
15. Pertanyaan
1 pointsDalam segitiga siku-siku ABC, besar sudut B = \(90^{\circ}\), \(\cos \text{A} = \dfrac{12}{13}\), dan panjang sisi BC = 25 cm. Luas segitiga ABC adalah …
Benar
Perhatikan gambar:
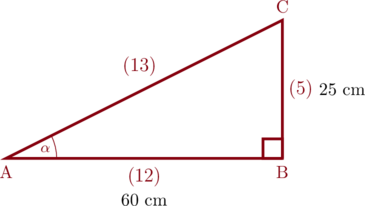
Luas segitiga ABC = ½ × AB × BC
Luas segitiga ABC = ½ × 60 cm × 25 cm
Luas segitiga ABC = 750 cm²
Salah
Perhatikan gambar:

Luas segitiga ABC = ½ × AB × BC
Luas segitiga ABC = ½ × 60 cm × 25 cm
Luas segitiga ABC = 750 cm²
-
Pertanyaan 16 dari 20
16. Pertanyaan
1 pointsPerhatikan gambar berikut:
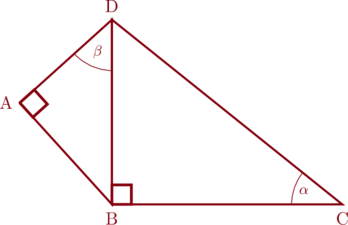
Jika panjang sisi DC = \(m\), maka panjang sisi AD = …
Benar
Lihat segitiga siku-siku DBC
\(\sin \alpha = \dfrac{\text{DB}}{\text{DC}}\)
\(\sin \alpha = \dfrac{\text{DB}}{m}\)
\(\text{DB} = m\cdot \sin \alpha\)
Lihat segitiga siku-siku BAD
\(\cos \beta = \dfrac{\text{AD}}{\text{DB}}\)
\(\cos \beta = \dfrac{\text{AD}}{m\cdot \sin \alpha}\)
\(\text{AD} = m\cdot \sin \alpha\cdot \cos \beta\)
Salah
Lihat segitiga siku-siku DBC
\(\sin \alpha = \dfrac{\text{DB}}{\text{DC}}\)
\(\sin \alpha = \dfrac{\text{DB}}{m}\)
\(\text{DB} = m\cdot \sin \alpha\)
Lihat segitiga siku-siku BAD
\(\cos \beta = \dfrac{\text{AD}}{\text{DB}}\)
\(\cos \beta = \dfrac{\text{AD}}{m\cdot \sin \alpha}\)
\(\text{AD} = m\cdot \sin \alpha\cdot \cos \beta\)
-
Pertanyaan 17 dari 20
17. Pertanyaan
1 pointsKoordinat kartesius titik \((2\sqrt{3}, 60^{\circ})\) adalah …
Benar
\(x = r\cdot \cos \theta\)
\(x = 2\sqrt{3}\cdot \frac{1}{2}\)
\(x = \sqrt{3}\)
\(y = r\cdot \sin \theta\)
\(y = 2\sqrt{3}\cdot \frac{1}{2}\sqrt{3}\)
\(y = 3\)
Jadi koordinat kartesiusnya adalah \((\sqrt{3}, 3)\)
Salah
\(x = r\cdot \cos \theta\)
\(x = 2\sqrt{3}\cdot \frac{1}{2}\)
\(x = \sqrt{3}\)
\(y = r\cdot \sin \theta\)
\(y = 2\sqrt{3}\cdot \frac{1}{2}\sqrt{3}\)
\(y = 3\)
Jadi koordinat kartesiusnya adalah \((\sqrt{3}, 3)\)
-
Pertanyaan 18 dari 20
18. Pertanyaan
1 pointsKoordinat polar dari titik \((9, 3\sqrt{3})\) adalah …
Benar
\(r = \sqrt{x^2 + y^2}\)
\(r = \sqrt{9^2 + (3\sqrt{3})^2}\)
\(r = \sqrt{81 + 27}\)
\(r = \sqrt{108}\)
\(r = 6\sqrt{3}\)
\(\tan \theta = \dfrac{y}{x}\)
\(\tan \theta = \dfrac{3\sqrt{3}}{9}\)
\(\tan \theta = \dfrac{1}{3}\sqrt{3}\)
\(\theta = 30^{\circ}\)
Jadi koordinat polarnya adalah \((6\sqrt{3}, 30^{\circ})\)
Salah
\(r = \sqrt{x^2 + y^2}\)
\(r = \sqrt{9^2 + (3\sqrt{3})^2}\)
\(r = \sqrt{81 + 27}\)
\(r = \sqrt{108}\)
\(r = 6\sqrt{3}\)
\(\tan \theta = \dfrac{y}{x}\)
\(\tan \theta = \dfrac{3\sqrt{3}}{9}\)
\(\tan \theta = \dfrac{1}{3}\sqrt{3}\)
\(\theta = 30^{\circ}\)
Jadi koordinat polarnya adalah \((6\sqrt{3}, 30^{\circ})\)
-
Pertanyaan 19 dari 20
19. Pertanyaan
1 pointsJika koordinat kutub titik \((m, 3)\) adalah \((r, 45^{\circ})\), maka nilai \(m + r = \dotso\)
Benar
\(y = r\cdot \sin \theta\)
\(3 = r \cdot \sin 45^{\circ}\)
\(3 = r \cdot \frac{1}{2}\sqrt{2}\)
\(r = \dfrac{3}{\frac{\sqrt{2}}{2}}\)
\(r = \dfrac{6}{\sqrt{2}}\times \color{red} \dfrac{\sqrt{2}}{\sqrt{2}}\)
\(r = 3\sqrt{2}\)
\(x = r\cdot \cos \theta\)
\(m = 3\sqrt{2} \cdot \cos 45^{\circ}\)
\(m = 3\sqrt{2} \cdot \frac{1}{2}\sqrt{2}\)
\(m = 3\)
Jadi nilai \(m + r = 3 + 3\sqrt{2}\)
Salah
\(y = r\cdot \sin \theta\)
\(3 = r \cdot \sin 45^{\circ}\)
\(3 = r \cdot \frac{1}{2}\sqrt{2}\)
\(r = \dfrac{3}{\frac{\sqrt{2}}{2}}\)
\(r = \dfrac{6}{\sqrt{2}}\times \color{red} \dfrac{\sqrt{2}}{\sqrt{2}}\)
\(r = 3\sqrt{2}\)
\(x = r\cdot \cos \theta\)
\(m = 3\sqrt{2} \cdot \cos 45^{\circ}\)
\(m = 3\sqrt{2} \cdot \frac{1}{2}\sqrt{2}\)
\(m = 3\)
Jadi nilai \(m + r = 3 + 3\sqrt{2}\)
-
Pertanyaan 20 dari 20
20. Pertanyaan
1 pointsPerhatikan gambar berikut!
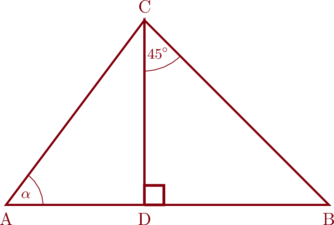
Jika \(\cos \alpha = \frac{2}{3}\), panjang AC = 21 cm, dan besar sudut BCD = 45°, maka panjang BC adalah …
Benar
Lihat segitiga siku-siku ADC,
\(\cos \alpha = \dfrac{\text{AD}}{\text{AC}}\)
\(\dfrac{2}{3} = \dfrac{\text{AD}}{21 \text{ cm}}\)
\(\text{AD} = \dfrac{42}{3} = 14 \text{ cm}\)
\(\text{DC} = \sqrt{(21)^2 \:-\: (14)^2}\)
\(\text{DC} = \sqrt{441 \:-\: 196}\)
\(\text{DC} = \sqrt{245}\)
\(\text{DC} = 7\sqrt{5}\text{ cm}\)
Lihat segitiga siku-siku BDC,
\(\sin \angle \text{BCD} = \dfrac{\text{DC}}{\text{BC}}\)
\(\sin 45^{\circ} = \dfrac{7\sqrt{5}}{\text{BC}}\)
\(\dfrac{\sqrt{2}}{2} = \dfrac{7\sqrt{5}}{\text{BC}}\)
\(2\cdot 7\sqrt{5} = \sqrt{2}\text{BC}\)
\(\dfrac{14\sqrt{5}}{\sqrt{2}} = \text{BC}\)
\(\text{BC} = \dfrac{14\sqrt{5}}{\sqrt{2}}\times \color{red} \dfrac{\sqrt{2}}{\sqrt{2}}\)
\(\text{BC} = \dfrac{14\sqrt{10}}{2} = 7\sqrt{10}\text{ cm}\)
Salah
Lihat segitiga siku-siku ADC,
\(\cos \alpha = \dfrac{\text{AD}}{\text{AC}}\)
\(\dfrac{2}{3} = \dfrac{\text{AD}}{21 \text{ cm}}\)
\(\text{AD} = \dfrac{42}{3} = 14 \text{ cm}\)
\(\text{DC} = \sqrt{(21)^2 \:-\: (14)^2}\)
\(\text{DC} = \sqrt{441 \:-\: 196}\)
\(\text{DC} = \sqrt{245}\)
\(\text{DC} = 7\sqrt{5}\text{ cm}\)
Lihat segitiga siku-siku BDC,
\(\sin \angle \text{BCD} = \dfrac{\text{DC}}{\text{BC}}\)
\(\sin 45^{\circ} = \dfrac{7\sqrt{5}}{\text{BC}}\)
\(\dfrac{\sqrt{2}}{2} = \dfrac{7\sqrt{5}}{\text{BC}}\)
\(2\cdot 7\sqrt{5} = \sqrt{2}\text{BC}\)
\(\dfrac{14\sqrt{5}}{\sqrt{2}} = \text{BC}\)
\(\text{BC} = \dfrac{14\sqrt{5}}{\sqrt{2}}\times \color{red} \dfrac{\sqrt{2}}{\sqrt{2}}\)
\(\text{BC} = \dfrac{14\sqrt{10}}{2} = 7\sqrt{10}\text{ cm}\)
