Nilai dari \(\dfrac{\sin 150^{\circ}\cdot \sec 45^{\circ}\cdot \tan 135^{\circ}}{\cos 120^{\circ}}\) adalah…
A. \(-\dfrac{1}{2}\)
B. \(\dfrac{1}{2}\)
C. \(-\sqrt{2}\)
D. \(\sqrt{2}\)
E. \(\dfrac{1}{2}\sqrt{2}\)
Jawaban: D
\(\sin 150^{\circ} = \sin (180^{\circ} \:-\:30^{\circ}) = +\sin 30^{\circ} = \dfrac{1}{2}\)
\(\sec 45^{\circ} = \sqrt{2}\)
\(\tan 135^{\circ} = \tan (180^{\circ} \:-\: 45^{\circ}) = -\tan 45^{\circ} = -1\)
\(\cos 120^{\circ} = \cos (180^{\circ} \:-\: 60^{\circ}) = -\cos 60^{\circ} = – \dfrac{1}{2}\)
\(\color{blue}\dfrac{\sin 150^{\circ}\cdot \sec 45^{\circ}\cdot \tan 135^{\circ}}{\cos 120^{\circ}}\)
\(\color{blue}= \dfrac{ \dfrac{1}{2}\cdot \sqrt{2}\cdot -1}{- \dfrac{1}{2}}\)
\(\color{blue}= \sqrt{2}\)
Nilai dari \(\dfrac{\cos 225^{\circ}\cdot \sec 330^{\circ} \cdot \tan 120^{\circ}}{\sin 315^{\circ}}\) adalah…
A. \(-2\)
B. \(-1\)
C. \(0\)
D. \(\dfrac{1}{2}\sqrt{3}\)
E. \(\dfrac{1}{3}\sqrt{3}\)
Jawaban: A
\(\cos 225^{\circ} = \cos (180^{\circ} + 45^{\circ}) = – \cos 45^{\circ} = -\dfrac{1}{2}\sqrt{2}\)
\(\sec 330^{\circ} = \sec (360^{\circ} \:-\: 30^{\circ}) = +\sec 30^{\circ} = +\dfrac{2}{3}\sqrt{3}\)
\(\tan 120^{\circ} = \tan(180^{\circ} \:-\: 60^{\circ}) = -\tan 60^{\circ} = -\sqrt{3}\)
\(\sin 315^{\circ} = \sin(360^{\circ} \:-\: 45^{\circ}) = -\sin 45^{\circ} = -\dfrac{1}{2}\sqrt{2}\)
\(\color{blue}\dfrac{\cos 225^{\circ}\cdot \sec 330^{\circ} \cdot \tan 120^{\circ}}{\sin 315^{\circ}}\)
\(\color{blue} = \dfrac{ \cancel{-\dfrac{1}{2}\sqrt{2}}\:\cdot \:\dfrac{2}{3}\sqrt{3}\:\cdot \: (-\sqrt{3})}{\cancel{-\dfrac{1}{2}\sqrt{2}}}\)
\(\color{blue} = -2\)
Nilai dari \(\dfrac{\sin \dfrac{\pi}{2} \cdot \cos \dfrac{2}{3}\pi \cdot \cot \dfrac{5}{4}\pi}{\cos \pi}\) adalah…
A. \(-1\)
B. \(1\)
C. \(0\)
D. \(\dfrac{1}{2}\)
E. \(\dfrac{1}{2}\sqrt{3}\)
Jawaban: D
\(\sin \dfrac{\pi}{2} = \sin (\dfrac{\cancel{\pi}}{2}\times \color{red}\dfrac{180^{\circ}}{\cancel{\pi}}\color{black}) = \sin 90^{\circ} = 1\)
\(\cos \dfrac{2}{3}\pi = \cos (\dfrac{2}{3}\cancel{\pi}\times \color{red}\dfrac{180^{\circ}}{\cancel{\pi}}\color{black}) = \cos 120^{\circ} = -\dfrac{1}{2}\)
\(\cot \dfrac{5}{4}\pi = \cot (\dfrac{5}{4}\cancel{\pi}\times \color{red}\dfrac{180^{\circ}}{\cancel{\pi}}\color{black}) =\cot 225^{\circ} = 1\)
\(\cos \pi = \cos (\cancel{\pi} \times \color{red}\dfrac{180^{\circ}}{\cancel{\pi}}\color{black})= \cos 180^{\circ} = -1\)
\(\color{blue}\dfrac{\sin \dfrac{\pi}{2} \cdot \cos \dfrac{2}{3}\pi \cdot \cot \dfrac{5}{4}\pi}{\cos \pi}\)
\(\color{blue} = \dfrac{1 \cdot (-\dfrac{1}{2}) \cdot 1}{-1}\)
\(\color{blue} = \dfrac{1}{2}\)
Nilai dari \(\sin (-210^{\circ}) + \tan (-45^{\circ}) \:-\: \cos (-300^{\circ})\) adalah…
A. \(-2\)
B. \(-1\)
C. \(0\)
D. \(\dfrac{1}{4}\)
E. \(2\dfrac{1}{2}\)
Jawaban: B
\(\color{purple} \sin (-\alpha) = -\sin \alpha\)
\(\color{purple} \tan (-\alpha) = -\tan \alpha\)
\(\color{purple} \cos (-\alpha) = \cos \alpha\)
\(\sin (-210^{\circ}) = – \sin{210^{\circ}} = -(-\dfrac{1}{2}) = +\dfrac{1}{2}\)
\(\tan (-45^{\circ}) = – \tan 45^{\circ} = -1\)
\(\cos (-300^{\circ}) = \cos 300^{\circ} = +\dfrac{1}{2}\)
\(\color{blue} \sin (-210^{\circ}) + \tan (-45^{\circ}) \:-\: \cos (-300^{\circ})\)
\(\color{blue} = \dfrac{1}{2} \:-\: 1 \:-\: \dfrac{1}{2} = -1\)
Nilai dari \(\dfrac{\sin 750^{\circ}-\cos 1080^{\circ} + \tan 1485^{\circ}}{\sec 1125^{\circ} \cdot \sin 1485^{\circ}}\) adalah…
A. \(-\dfrac{1}{2}\)
B. \(\dfrac{1}{2}\)
C. \(1\)
D. \(2\)
E. \(4\)
Jawaban: B
\(\sin 750^{\circ} = \sin(2\cdot 360^{\circ} + \color{red}30^{\circ}\color{black}) = \sin 30^{\circ} = \dfrac{1}{2}\)
\(\cos 1080^{\circ} = \cos (3\cdot 360^{\circ} + \color{red} 0^{\circ}\color{black}) = \cos 0^{\circ} = 1\)
\(\tan 1485^{\circ} = \tan(8\cdot 180^{\circ} + \color{red}45^{\circ}\color{black}) = \tan 45^{\circ} = 1\)
\(\sec 1125^{\circ} = \sec(3 \cdot 360^{\circ} + \color{red}45^{\circ}\color{black}) = \sec 45^{\circ} = \sqrt{2}\)
\(\sin 1485^{\circ} = \sin(4 \cdot 360^{\circ} + \color{red}45^{\circ}\color{black}) = \sin 45^{\circ} = \dfrac{1}{2}\sqrt{2}\)
\(\color{blue}\dfrac{\sin 750^{\circ} \:-\:\cos 1080^{\circ} + \tan 1485^{\circ}}{\sec 1125^{\circ} \cdot \sin 1485^{\circ}}\)
\(\color{blue} = \dfrac{\dfrac{1}{2} \:-\: 1 + 1}{\sqrt{2}\cdot \dfrac{1}{2}\sqrt{2}}\)
\(\color{blue} = \dfrac{\dfrac{1}{2} }{1}\)
\(\color{blue} = \dfrac{1}{2}\)
Nilai dari \(\dfrac{\sin \dfrac{\pi}{6} + \cos \pi \cdot \cos \dfrac{5\pi}{3} + \cot \dfrac{3\pi}{4}}{\sec \dfrac{\pi}{3}\cdot \sin \dfrac{25\pi}{6}}\) adalah…
A. \(-1\)
B. \(1\)
C. \(0\)
D. \(1\)
E. \(2\)
Jawaban: A
\(\sin \dfrac{\pi}{6} = \sin (\dfrac{\cancel{\pi}}{6}\times \color{red}\dfrac{180^{\circ}}{\cancel{\pi}}\color{black}) = \sin 30^{\circ} = \dfrac{1}{2}\)
\(\cos \pi = \cos (\cancel{\pi}\times \color{red}\dfrac{180^{\circ}}{\cancel{\pi}}\color{black}) = \cos 180^{\circ} = -1\)
\(\cos \dfrac{5\pi}{3} = \cos (\dfrac{5\cancel{\pi}}{3}\times \color{red}\dfrac{180^{\circ}}{\cancel{\pi}}\color{black}) = \cos 300^{\circ} = \dfrac{1}{2}\)
\(\cot\dfrac{3\pi}{4} = \cot (\dfrac{3\cancel{\pi}}{4}\times \color{red}\dfrac{180^{\circ}}{\cancel{\pi}}\color{black}) = \cot 135^{\circ} = -1\)
\(\sec \dfrac{\pi}{3} = \sec (\dfrac{\cancel{\pi}}{3}\times \color{red}\dfrac{180^{\circ}}{\cancel{\pi}}\color{black}) = \sec 60^{\circ} = 2\)
\(\sin \dfrac{25\pi}{6} = \sec (\dfrac{25\cancel{\pi}}{6}\times \color{red}\dfrac{180^{\circ}}{\cancel{\pi}}\color{black}) = \sin 750^{\circ} = \dfrac{1}{2}\)
\(\color{blue}\dfrac{\sin \dfrac{\pi}{6} + \cos \pi \cdot \cos \dfrac{5\pi}{3} + \cot \dfrac{3\pi}{4}}{\sec \dfrac{\pi}{3}\cdot \sin \dfrac{25\pi}{6}}\)
\(\color{blue} = \dfrac{\dfrac{1}{2} + (-1) \cdot \dfrac{1}{2} + (-1)}{2\cdot \dfrac{1}{2}}\)
\(\color{blue} = \dfrac{-1}{1}\)
\(\color{blue} = -1\)
Nilai dari \(\dfrac{\sin(-1230^{\circ})\cdot \tan(-1215^{\circ})}{\sec(-1680^{\circ})}\) adalah…
A. \(-\dfrac{1}{4}\)
B. \(\dfrac{1}{4}\)
C. \(\dfrac{1}{8}\)
D. \(1\)
E. \(2\)
Jawaban: B
\(\sin(-1230^{\circ}) = -\sin 1230^{\circ} = -\sin(3\cdot 360^{\circ} + \color{red} 150^{\circ}\color{black}) = -\sin 150^{\circ} = -\dfrac{1}{2}\)
\(\tan(-1215^{\circ}) = -\tan 1215^{\circ} = – \tan(6 \cdot 180^{\circ} + \color{red} 135^{\circ}\color{black}) = -\tan 135^{\circ} = -(-1) = 1\)
\(\sec(-1680^{\circ}) = \sec 1680^{\circ}= \sec (4 \cdot 360^{\circ} + \color{red} 240^{\circ}\color{black}) = \sec 240^{\circ} = -2\)
\(\color{blue}\dfrac{\sin(-1230^{\circ})\cdot \tan(-1215^{\circ})}{\sec(-1680^{\circ})}\)
\(\color{blue} = \dfrac{ -\dfrac{1}{2}\cdot 1}{ -2}\)
\(\color{blue} = \dfrac{1}{4}\)
Jika \(\tan 25^{\circ} = p\), maka \(\dfrac{\sin 205^{\circ}\cdot \sec 335^{\circ}}{\sin 330^{\circ}}=\dotso\)
A. \(-p\)
B. \(-2p\)
C. \(2p\)
D. \(4p\)
E. \(5p\)
Jawaban: C
\(\tan 25^{\circ} = \dfrac{p}{1} = \dfrac{\text{depan}}{\text{samping}}\)
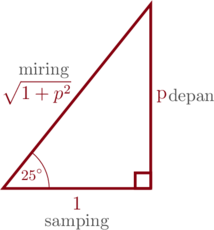
\(\sin 205^{\circ} = \sin (180^{\circ} + 25^{\circ}) = -\sin 25^{\circ} = -\dfrac{p}{\sqrt{1 + p^2}}\)
\(\sec 335^{\circ} = \sec(360^{\circ} \:-\: 25^{\circ}) = \sec 25^{\circ} = \dfrac{\sqrt{1 + p^2}}{1}\)
\(\sin 330^{\circ} = \sin(360^{\circ} \:-\: 30^{\circ}) = -\sin 30^{\circ} = -\dfrac{1}{2}\)
\(\color{blue}\dfrac{\sin 205^{\circ}\cdot \sec 335^{\circ}}{\sin 330^{\circ}}\)
\(\color{blue} = \dfrac{-\dfrac{p}{\cancel{\sqrt{1 + p^2}}}\cdot \dfrac{\cancel{\sqrt{1 + p^2}}}{1}}{-\dfrac{1}{2}}\)
\(\color{blue} = \dfrac{-p}{-\dfrac{1}{2}}\)
\(\color{blue} = 2p\)
Jika \(\sin 25^{\circ} = \dfrac{2m}{m^2 + 1}, m > 1\) maka \(\sec 335^{\circ} + \cot 245^{\circ} = \dotso\)
A. \(\dfrac{m^2 + 1}{2m}\)
B. \(\dfrac{m^2 + 1}{m^2 \:-\: 1}\)
C. \(\dfrac{m^2}{m^2 \:-\: 1}\)
D. \(\dfrac{2m^3 + 2}{m^2 \:-\: 1}\)
E. \(\dfrac{m + 1}{m \:-\: 1}\)
Jawaban: E
\(\sin 25^{\circ} = \dfrac{2m}{m^2 + 1} = \dfrac{\text{depan}}{\text{miring}}\)
Sisi samping dicari menggunakan rumus pythagoras
\(\text{Sisi samping} = \sqrt{(m^2 + 1)^2 \:-\: (2m)^2}\)
\(= \sqrt{m^4 + 2m^2 + 1 \:-\: 4m^2}\)
\(= \sqrt{m^4 \:-\:2m^2 + 1 }\)
\(= \sqrt{(m^2 \:-\: 1)^2 } = m^2 \:-\: 1\)
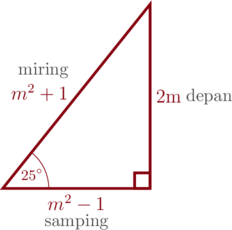
\(\sec 335^{\circ} = \sec (360^{\circ} \:-\: 25^{\circ}) = \sec 25^{\circ} = \dfrac{m^2 + 1}{m^2 \:-\: 1}\)
\(\cot 245^{\circ} = \cot(270^{\circ} \:-\: 25^{\circ}) = \tan 25^{\circ} = \dfrac{2m}{m^2 \:-\: 1}\)
\(\color{blue}\sec 335^{\circ} + \cot 245^{\circ}\)
\(\color{blue} = \dfrac{m^2 + 1}{m^2 \:-\: 1} + \dfrac{2m}{m^2 \:-\: 1}\)
\(\color{blue} = \dfrac{m^2 + 2m + 1}{m^2 \:-\: 1}\)
\(\color{blue} = \dfrac{\cancel{(m + 1)}(m + 1)}{\cancel{(m + 1)}(m \:-\: 1)}\)
\(\color{blue} = \dfrac{m + 1}{m \:-\: 1}\)
Diketahui \(\sin \alpha = -\dfrac{1}{5}, \: \dfrac{\pi}{2} < \alpha < \dfrac{3}{2}\pi\), dan \(\cos \beta = \dfrac{3}{5}, \: \pi < \beta < 2\pi\), nilai dari \(16\tan \alpha \cdot \cot \beta = \dotso\)
A. \(- \sqrt{5}\)
B. \(- \sqrt{6}\)
C. \(\sqrt{5}\)
D. \(\sqrt{6}\)
E. \(2\sqrt{5}\)
Jawaban: B
Karena \(\sin \alpha\) bernilai negatif dan \(\dfrac{\pi}{2} < \alpha < \dfrac{3}{2}\pi\), maka \(\alpha\) terletak dikuadran III
Karena \(\cos \beta \) bernilai positif dan \(\pi < \beta < 2\pi\), maka \(\beta\) terletak dikuadran IV
Kita gambar dua buah segitiga siku-siku yang masing-masing bersudut \(\alpha\) dan \(\beta\)
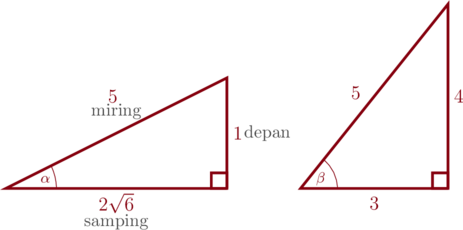
\(\color{blue} 16\cdot \tan \alpha \cdot \cot \beta\)
\(\color{blue} = 16 \cdot \dfrac{1}{2\sqrt{6}} \cdot (-\dfrac{3}{4})\)
\(\color{blue} = 16 \cdot \dfrac{1}{2\sqrt{6}}\times \color{red}\dfrac{\sqrt{6}}{\sqrt{6}} \color{blue}\cdot (-\dfrac{3}{4})\)
\(\color{blue} = 16 \cdot \dfrac{1}{12}\sqrt{6}\cdot (-\dfrac{3}{4})\)
\(\color{blue} = – \cancel{16}\cdot \dfrac{3}{\cancelto{3}{48}}\sqrt{6}\)
\(\color{blue} = – \sqrt{6}\)
