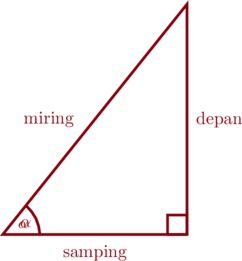
| Perbandingan Trigonometri | |
| $$\sin \alpha = \dfrac{\text{depan}}{\text{miring}}$$ | $$\csc \alpha = \dfrac{\text{miring}}{\text{depan}}$$ |
| $$\cos \alpha = \dfrac{\text{samping}}{\text{miring}}$$ | $$\sec\alpha = \dfrac{\text{miring}}{\text{samping}}$$ |
| $$\tan \alpha = \dfrac{\text{depan}}{\text{samping}}$$ | $$\cot \alpha = \dfrac{\text{samping}}{\text{depan}}$$ |
| Sudut Istimewa | |||||
| $$0^{\circ}$$ | $$30^{\circ}$$ | $$45^{\circ}$$ | $$60^{\circ}$$ | $$90^{\circ}$$ | |
| sin | $$0$$ | $$\dfrac{1}{2}$$ | $$\dfrac{1}{2}\sqrt{2}$$ | $$\dfrac{1}{2}\sqrt{3}$$ | $$1$$ |
| cos | $$1$$ | $$\dfrac{1}{2}\sqrt{3}$$ | $$\dfrac{1}{2}\sqrt{2}$$ | $$\dfrac{1}{2}$$ | $$0$$ |
| tan | $$0$$ | $$\dfrac{1}{3}\sqrt{3}$$ | $$1$$ | $$\sqrt{3}$$ | $$\infty$$ |
| csc | $$\infty$$ | $$2$$ | $$\sqrt{2}$$ | $$\dfrac{2}{3}\sqrt{3}$$ | $$1$$ |
| sec | $$1$$ | $$\dfrac{2}{3}\sqrt{3}$$ | $$\sqrt{2}$$ | $$2$$ | $$\infty$$ |
| cot | $$\infty$$ | $$\sqrt{3}$$ | $$1$$ | $$\dfrac{1}{3}\sqrt{3}$$ | $$0$$ |
IDENTITAS DASAR
\(\color{blue}\tan \alpha = \dfrac{\sin \alpha}{\cos \alpha}\)
\(\color{blue}\cot \alpha = \dfrac{1}{\tan \alpha}\)
\(\color{blue}\sec \alpha = \dfrac{1}{\cos \alpha}\)
\(\color{blue}\csc\alpha = \dfrac{1}{\sin \alpha}\)
Contoh Soal
Tentukan perbandingan trigonometri untuk sudut \(\alpha\) pada segitiga ABC berikut ini.

Panjang sisi AC dapat kita cari menggunakan rumus pythagoras
\(\text{AB}^2 + \text{BC}^2 = \text{AC}^2\)
\(3^2 + 4^2 = \text{AC}^2\)
\(9 + 16 = \text{AC}^2\)
\(25 = \text{AC}^2\)
\(\text{AC} = \sqrt{25} = 5\)
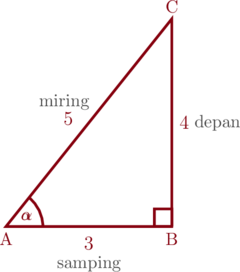
- \(\sin \alpha = \dfrac{\text{de}}{\text{mi}} = \dfrac{4}{5}\)
- \(\cos \alpha = \dfrac{\text{sa}}{\text{mi}}= \dfrac{3}{5}\)
- \(\tan \alpha = \dfrac{\text{de}}{\text{sa}}= \dfrac{4}{3}\)
- \(\csc \alpha = \dfrac{\text{mi}}{\text{de}}= \dfrac{5}{4}\)
- \(\sec\alpha = \dfrac{\text{mi}}{\text{sa}} = \dfrac{5}{3}\)
- \(\cot \alpha = \dfrac{\text{sa}}{\text{de}} = \dfrac{3}{4}\)
Tentukan perbandingan trigonometri untuk sudut \(\beta\) pada segitiga ABC berikut ini.

Panjang sisi BC dapat kita cari menggunakan rumus pythagoras
\(\text{AB}^2 + \text{BC}^2 = \text{AC}^2\)
\((2\sqrt{2})^2 + \text{BC}^2 = (2\sqrt{5})^2\)
\(8 + \text{BC}^2 = 20\)
\(\text{BC}^2 = 20-8\)
\(\text{BC}^2 = 12\)
\(\text{BC} = \sqrt{12}\)
\(\text{BC} = \sqrt{4\times 3}\)
\(\text{BC} = 2\sqrt{3}\)
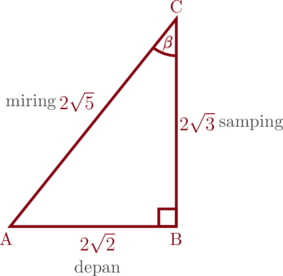
- \(\sin \beta = \dfrac{\text{de}}{\text{mi}} = \dfrac{\cancel{2}\sqrt{2}}{\cancel{2}\sqrt{5}}\times \color{blue}\dfrac{\sqrt{5}}{\sqrt{5}}=\color{black}\dfrac{\sqrt{10}}{5}\)
- \(\cos \beta = \dfrac{\text{sa}}{\text{mi}}= \dfrac{\cancel{2}\sqrt{3}}{\cancel{2}\sqrt{5}}\times \color{blue}\dfrac{\sqrt{5}}{\sqrt{5}}=\color{black}\dfrac{\sqrt{15}}{5}\)
- \(\tan \beta = \dfrac{\text{de}}{\text{sa}}= \dfrac{\cancel{2}\sqrt{2}}{\cancel{2}\sqrt{3}}\times \color{blue}\dfrac{\sqrt{3}}{\sqrt{3}}=\color{black}\dfrac{\sqrt{6}}{3}\)
- \(\csc \beta = \dfrac{\text{mi}}{\text{de}}= \dfrac{\cancel{2}\sqrt{5}}{\cancel{2}\sqrt{2}}\times \color{blue}\dfrac{\sqrt{2}}{\sqrt{2}}=\color{black}\dfrac{\sqrt{10}}{2}\)
- \(\sec\beta = \dfrac{\text{mi}}{\text{sa}} = \dfrac{\cancel{2}\sqrt{5}}{\cancel{2}\sqrt{3}}\times \color{blue}\dfrac{\sqrt{3}}{\sqrt{3}}=\color{black}\dfrac{\sqrt{15}}{3}\)
- \(\cot \beta = \dfrac{\text{sa}}{\text{de}} = \dfrac{\cancel{2}\sqrt{3}}{\cancel{2}\sqrt{2}}\times \color{blue}\dfrac{\sqrt{2}}{\sqrt{2}}=\color{black}\dfrac{\sqrt{6}}{2}\)
Tentukan perbandingan trigonometri untuk sudut \(\gamma\) pada segitiga ABC berikut ini.
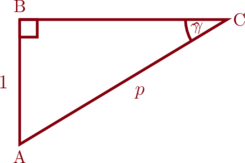
Panjang sisi BC dapat kita cari menggunakan rumus pythagoras
\(\text{AB}^2 + \text{BC}^2 = \text{AC}^2\)
\(1^2 + \text{BC}^2 = p^2\)
\(1 + \text{BC}^2 = p^2\)
\(\text{BC}^2 = p^2-1\)
\(\text{BC} = \sqrt{p^2-1}\)
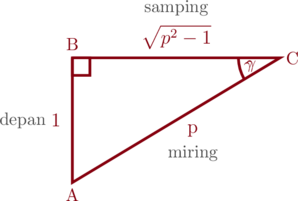
- \(\sin \gamma = \dfrac{\text{de}}{\text{mi}} = \dfrac{1}{p}\)
- \(\cos \gamma = \dfrac{\text{sa}}{\text{mi}}= \dfrac{\sqrt{p^2 – 1}}{p}\)
- \(\tan \gamma = \dfrac{\text{de}}{\text{sa}}= \dfrac{1}{\sqrt{p^2 – 1}}\)
- \(\csc \gamma = \dfrac{\text{mi}}{\text{de}}= \dfrac{p}{1} = p\)
- \(\sec\gamma = \dfrac{\text{mi}}{\text{sa}} = \dfrac{p}{\sqrt{p^2 – 1}}\)
- \(\cot \gamma = \dfrac{\text{sa}}{\text{de}} = \dfrac{\sqrt{p^2 – 1}}{1} =\sqrt{p^2 – 1} \)
Pada gambar segitiga di bawah ini, panjang sisi BD = 8 cm, besar \(\angle \text{BDA} = 45^{\circ}\), dan besar \(\angle \text{BCA} = 30^{\circ}\)
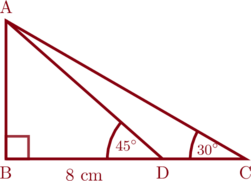
Tentukan panjang sisi:
a. \(\text{AB}\)
b. \(\text{AC}\)
c. \(\text{DC}\)
Mencari panjang AB
Lihat segitiga siku-siku ABD
\(\tan 45^{\circ} = \dfrac{\text{de}}{\text{sa}}=\dfrac{\text{AB}}{\text{BD}}\)
\(1 = \dfrac{\text{AB}}{8}\)
\(\text{AB} = 8 \text{ cm}\)
Mencari panjang AC
Lihat segitiga siku-siku ABC
\(\sin 30^{\circ} = \dfrac{\text{de}}{\text{mi}} = \dfrac{\text{AB}}{\text{AC}}\)
\(\dfrac{1}{2} = \dfrac{8}{\text{AC}}\)
\(\text{AC} = 16 \text{ cm}\)
Mencari panjang DC
Lihat segitiga siku-siku ABC, kita dapat mencari panjang BC terlebih dahulu
\(\tan 30^{\circ} = \dfrac{\text{de}}{\text{sa}} = \dfrac{\text{AB}}{\text{BC}}\)
\(\dfrac{\sqrt{3}}{3} = \dfrac{8}{\text{BC}}\)
\(\sqrt{3}\cdot \text{BC} = 24\)
\(\text{BC} = \dfrac{24}{\sqrt{3}} \times \color{blue} \dfrac{\sqrt{3}}{\sqrt{3}}\)
\(\text{BC} = \dfrac{24\sqrt{3}}{3}\)
\(\text{BC} = 8\sqrt{3}\)
\(\text{DC = BC – BD}\)
\(\text{DC} = 8\sqrt{3} – 8 \text{ cm}\)
Pada gambar segitiga di bawah ini, panjang sisi AD = 10 cm, besar \(\angle \text{BAC} = 30^{\circ}\), dan besar \(\angle \text{BDC} = 60^{\circ}\)

Tentukan panjang sisi:
a. \(\text{DB}\)
b. \(\text{BC}\)
c. \(\text{AC}\)
Mencari Panjang DB
Perhatikan segitiga siku-siku DBC
\(\tan 60^{\circ} = \dfrac{\text{BC}}{\text{DB}}\)
\(\sqrt{3} = \dfrac{\text{BC}}{\text{DB}}\)
\(\text{BC} = \sqrt{3}\cdot\text{DB}\dotso\dotso(1)\)
Perhatikan segitiga siku-siku ABC
\(\tan 30^{\circ} = \dfrac{\text{BC}}{\text{AB}}\:\:\:\:\:\color{blue} \text{substitusikan BC dari persamaan 1}\)
\(\dfrac{\sqrt{3}}{3} = \dfrac{ \sqrt{3}\cdot\text{DB}}{10 + \text{DB}}\)
\(\dfrac{\cancel{\sqrt{3}}}{3} = \dfrac{\cancel{ \sqrt{3}}\cdot\text{DB}}{10 + \text{DB}}\)
\(\dfrac{1}{3} = \dfrac{\text{DB}}{10 + \text{DB}}\:\:\:\:\:\color{blue}\text{kali silang}\)
\(10 + \text{DB} = 3\text{DB}\)
\(10 = 3\text{DB} – \text{DB} \)
\(10 = 2\text{DB}\)
\(\text{DB} = \dfrac{10}{2} = 5 \text{ cm}\)
Mencari Panjang BC
\(\text{Dari persamaan 1:}\)
\(\text{BC} = \sqrt{3}\cdot\text{DB}\)
\(\text{BC} = \sqrt{3}\times 5\)
\(\text{BC} = 5\sqrt{3}\text{ cm}\)
Mencari Panjang AC
Lihat segitiga siku-siku ABC
\(\sin 30^{\circ} = \dfrac{\text{BC}}{\text{AC}}\)
\(\dfrac{1}{2} = \dfrac{ 5\sqrt{3}}{\text{AC}}\:\:\:\:\:\color{blue}\text{kali silang}\)
\(\text{AC} = 2\times 5\sqrt{3}\)
\(\text{AC} = 10\sqrt{3}\text{ cm}\)
Pada gambar segitiga di bawah ini, panjang sisi BC = \(10\sqrt{2}\) cm, besar \(\angle \text{BAE} = 60^{\circ}\), dan besar \(\angle \text{BCE} = 45^{\circ}\)
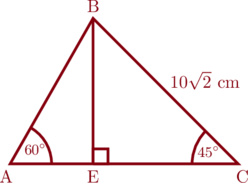
Tentukan panjang sisi:
a. \(\text{BE}\)
b. \(\text{AB}\)
c. \(\text{AC}\)
Mencari Panjang BE
Lihat segitiga siku-siku BEC
\(\sin 45^{\circ} = \dfrac{\text{BE}}{\text{BC}}\)
\(\dfrac{\sqrt{2}}{2} = \dfrac{\text{BE}}{10\sqrt{2}}\:\:\:\:\:\color{blue}\text{kalikan silang}\)
\(\sqrt{2}\times 10\sqrt{2} = 2 \times \text{BE}\)
\(\cancel{2}\times 10 = \cancel{2} \times \text{BE}\)
\(\text{BE} = 10 \text{ cm}\)
Panjang \(\text{EC = BE}\) karena \(\triangle \text{BEC}\) adalah segitiga sama kaki
Mencari Panjang AB
Lihat segitiga siku-siku AEB
\(\sin 60^{\circ} = \dfrac{\text{BE}}{\text{AB}}\)
\(\dfrac{\sqrt{3}}{2}= \dfrac{10}{\text{AB}}\:\:\:\:\:\color{blue}\text{kalikan silang}\)
\(\sqrt{3}\cdot\text{AB} = 20\)
\(\text{AB} = \dfrac{20}{\sqrt{3}}\)
\(\text{AB} = \dfrac{20}{\sqrt{3}}\times \color{blue} \dfrac{\sqrt{3}}{\sqrt{3}}\)
\(\text{AB} = \dfrac{20}{3}\sqrt{3}\text{ cm}\)
Mencari Panjang AC
Lihat segitiga siku-siku AEB
Kita cari dahulu panjang AE,
\(\cos 60^{\circ} = \dfrac{\text{AE}}{\text{AB}}\)
\(\dfrac{1}{2} = \dfrac{\text{AE}}{\dfrac{20}{3}\sqrt{3}}\)
\(\dfrac{1}{2} = \dfrac{3\text{AE}}{20\sqrt{3}}\:\:\:\:\:\color{blue}\text{kalikan silang}\)
\(\cancelto{10}{20}\sqrt{3} = \cancel{2} \times 3\text{AE}\)
\(10\sqrt{3} = 3\text{AE}\)
\(\text{AE} = \dfrac{10\sqrt{3} }{3} \text{ cm}\)
\(\text{AC} = \text{AE} + \text{EC}\)
\(\text{AC} = \dfrac{10\sqrt{3} }{3} +10 \text{ cm}\)
Galvin berdiri pada jarak \(11\sqrt{3}\) meter dari tiang bendera, dan memandang puncak tiang bendera itu dengan sudut elevasi \(30^{\circ}\). Diketahui jarak mata Galvin diukur dari permukaan tanah adalah \(150\) cm. Hitunglah tinggi tiang bendera tersebut.
Perhatikan gambar di bawah ini
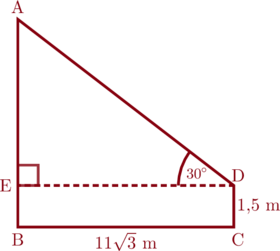
Jarak mata Galvin diukur dari permukaan tanah adalah \(\text{DC} = 150 \text{ cm} = 1,5 \text{ m}\)
Jarak antara Galvin dengan tiang bendera adalah \(\text{BC} = 11\sqrt{3}\) m
Tinggi tiang bendera adalah \(\text{AB}\)
Untuk mencari tinggi tiang bendera, perhatikan \(\triangle \text{AED}\)
\(\tan 30^{\circ} = \dfrac{\text{AE}}{\text{ED}}\)
\(\dfrac{1}{\sqrt{3}} = \dfrac{\text{AE}}{11\sqrt{3}}\:\:\:\:\:\color{blue}\text{kalikan silang}\)
\(11\cancel{\sqrt{3}} = \cancel{\sqrt{3}}\cdot \text{AE}\)
\(\text{AE} = 11 \text{ m}\)
\(\text{AB} = \text{AE} + \text{EB}\)
\(\text{AB} = 11 + 1,5\)
\(\text{AB} = 12,5 \text{ m}\)
Jadi tinggi tiang bendera tersebut adalah \(12,5 \text{ m}\)
Joko akan mengukur tinggi sebuah tower menggunakan klinometer. Saat pertama berdiri dengan melihat puncak tower, terlihat pada klinometer menunjuk pada sudut \(60^{\circ}\). Kemudian dia bergerak menjauhi tower sejauh 20 meter dan terlihat pada klinometer sudut \(45^{\circ}\). Hitunglah tinggi tower tersebut.
Perhatikan gambar di bawah ini
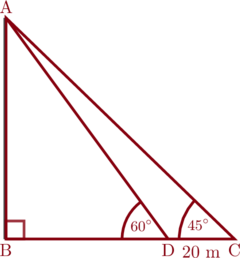
Langkah mencari tinggi tower \(\text{AB}\)
Perhatikan \(\triangle \text{ABD}\)
\(\tan 60^{\circ} = \dfrac{\text{AB}}{\text{BD}}\)
\(\sqrt{3} = \dfrac{\text{AB}}{\text{BD}}\)
\(\text{AB} = \sqrt{3}\cdot \text{BD}\)
Perhatikan \(\triangle \text{ABC}\)
\(\tan 45^{\circ} = \dfrac{\text{AB}}{\text{BC}}\)
\(1 = \dfrac{\text{AB}}{\text{BC}}\)
\(\text{BC} = \text{AB}\)
\(\text{BD} + 20 = \sqrt{3}\cdot\text{BD}\)
\(20 = \sqrt{3}\cdot\text{BD} – \text{BD}\)
\(20 = (\sqrt{3} – 1)\text{BD}\)
\(\text{BD} = \dfrac{20}{\sqrt{3} – 1} \times \color{blue} \dfrac{\sqrt{3} + 1}{\sqrt{3} + 1}\)
\(\text{BD} = \dfrac{20(\sqrt{3} + 1)}{3 – 1}\)
\(\text{BD} = \dfrac{20\sqrt{3} + 20)}{2}\)
\(\text{BD} = 10\sqrt{3} + 10 \text{ m}\)
\(\text{AB} = \sqrt{3}\cdot\text{BD}\)
\(\text{AB} = \sqrt{3}(10\sqrt{3} + 10)\)
\(\text{AB} = 30 + 10\sqrt{3}\text{ m}\)
Jadi tinggi tower tersebut adalah \(30 + 10\sqrt{3}\text{ m}\)
