Sebelum kita belajar tentang relasi sudut dalam trigonometri, kita pahami terlebih dahulu tentang letak kuadran yang berpengaruh pada nilai fungsi trigonometri
Letak Kuadran
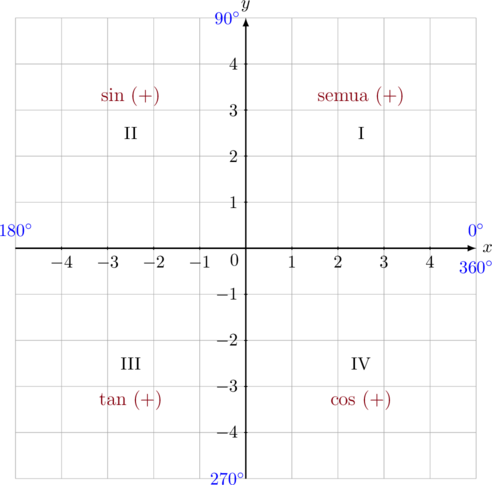
Keterangan:
- Pada kuadran I \([0^{\circ} – 90^{\circ}]\) semua fungsi trigonometri bernilai positif
- Pada kuadran II \([90^{\circ} – 180^{\circ}]\) fungsi sinus dan juga cosecan bernilai positif, fungsi trigonometri yang lainnya bernilai negatif
- Pada kuadran III \([180^{\circ} – 270^{\circ}]\) fungsi tangen dan juga cotangen bernilai positif, fungsi trigonometri yang lainnya bernilai negatif
- Pada kuadran IV \([270^{\circ} – 360^{\circ}]\) fungsi cosinus dan juga secan bernilai postif, fungsi trigonometri yang lainnya bernilai negatif
Relasi Sudut \((90^{\circ} -\: \alpha)\) dan \((90^{\circ} + \alpha)\)
\(\text{Fungsi trigonometri berubah}\)
| \((90^{\circ} -\: \alpha)\) | \((90^{\circ} + \alpha)\) |
| $$\sin (90^{\circ} -\:\alpha) = \cos \alpha$$ | $$\sin (90^{\circ} +\:\alpha) =\: \cos \alpha$$ |
| $$\cos (90^{\circ} -\:\alpha) = \sin \alpha$$ | $$\cos (90^{\circ} +\:\alpha) = -\sin \alpha$$ |
| $$\tan (90^{\circ} -\:\alpha) = \cot \alpha$$ | $$\tan (90^{\circ} +\:\alpha) = -\cot \alpha$$ |
| $$\csc (90^{\circ} -\:\alpha) = \sec \alpha$$ | $$\csc (90^{\circ} +\:\alpha) = \:\sec \alpha$$ |
| $$\sec (90^{\circ} -\:\alpha) = \csc \alpha$$ | $$\sec (90^{\circ} +\:\alpha) = -\csc \alpha$$ |
| $$\cot (90^{\circ} -\:\alpha) = \tan \alpha$$ | $$\cot (90^{\circ} +\:\alpha) = -\tan \alpha$$ |
Contoh:
- \(\sin{30^{\circ}} = \sin{(90^{\circ} – 60^{\circ})} = +\cos 60^{\circ} = +\dfrac{1}{2}\)
\(\sin{30^{\circ}}\) berada di kuadran I sehingga nilainya positif
- \(\cos{45^{\circ}} = \cos{(90^{\circ} – 45^{\circ})} = +\sin 45^{\circ} = +\dfrac{1}{2}\sqrt{2}\)
\(\cos{45^{\circ}}\) berada di kuadran I sehingga nilainya positif
- \(\tan{60^{\circ}} = \tan{(90^{\circ} – 30^{\circ})} = +\cot 30^{\circ} = +\sqrt{3}\)
\(\tan{60^{\circ}}\) berada di kuadran I sehingga nilainya positif
- \(\sin{120^{\circ}} = \sin{(90^{\circ} + 30^{\circ})} = +\cos 30^{\circ} = +\dfrac{1}{2}\sqrt{3}\)
\(\sin{120^{\circ}}\) berada di kuadran II sehingga nilainya positif
- \(\cos{150^{\circ}} = \cos{(90^{\circ} + 60^{\circ})} = -\sin 60^{\circ} = -\dfrac{1}{2}\sqrt{3}\)
\(\cos{150^{\circ}}\) berada di kuadran II sehingga nilainya negatif
- \(\tan{135^{\circ}} = \tan{(90^{\circ} + 45^{\circ})} = -\cot 45^{\circ} = -1\)
\(\tan{135^{\circ}}\) berada di kuadran II sehingga nilainya negatif
Relasi Sudut \((180^{\circ} -\: \alpha)\) dan \((180^{\circ} + \alpha)\)
\(\text{Fungsi trigonometri tetap}\)
| \((180^{\circ} -\: \alpha)\) | \((180^{\circ} + \alpha)\) |
| $$\sin (180^{\circ} -\:\alpha) = \:\sin\alpha$$ | $$\sin (180^{\circ} +\:\alpha) =-\sin\alpha$$ |
| $$\cos (180^{\circ} -\:\alpha) = -\cos \alpha$$ | $$\cos (180^{\circ} +\:\alpha) = -\cos \alpha$$ |
| $$\tan (180^{\circ} -\:\alpha) = -\tan\alpha$$ | $$\tan (180^{\circ} +\:\alpha) = \:\tan \alpha$$ |
| $$\csc (180^{\circ} -\:\alpha) = \:\csc \alpha$$ | $$\csc (180^{\circ} +\:\alpha) = -\csc \alpha$$ |
| $$\sec (180^{\circ} -\:\alpha) = -\sec \alpha$$ | $$\sec (180^{\circ} +\:\alpha) = -\sec \alpha$$ |
| $$\cot (180^{\circ} -\:\alpha) = -\cot\alpha$$ | $$\cot (180^{\circ} +\:\alpha) = \:\cot \alpha$$ |
Contoh:
- \(\sin{135^{\circ}} = \sin{(180^{\circ} – 45^{\circ})} = +\sin 45^{\circ} = +\dfrac{1}{2}\sqrt{2}\)
\(\sin{135^{\circ}}\) berada di kuadran II sehingga nilainya positif
- \(\sec{150^{\circ}} = \sec{(180^{\circ} – 30^{\circ})} = -\sec 30^{\circ} = -\dfrac{2}{3}\sqrt{3}\)
\(\sec{150^{\circ}}\) berada di kuadran II sehingga nilainya negatif
- \(\csc{120^{\circ}} = \csc{(180^{\circ} – 60^{\circ})} = +\csc 60^{\circ} = +\dfrac{2}{3}\sqrt{3}\)
\(\csc{120^{\circ}}\) berada di kuadran II sehingga nilainya positif
- \(\tan{225^{\circ}} = \tan{(180^{\circ} + 45^{\circ})} = +\tan 45^{\circ} = +1\)
\(\tan{225^{\circ}}\) berada di kuadran III sehingga nilainya positif
- \(\cos{210^{\circ}} = \cos{(180^{\circ} + 30^{\circ})} = -\cos 30^{\circ} = -\dfrac{1}{2}\sqrt{3}\)
\(\cos{210^{\circ}}\) berada di kuadran III sehingga nilainya negatif
- \(\sin{240^{\circ}} = \sin{(180^{\circ} + 60^{\circ})} = -\sin 60^{\circ} =-\dfrac{1}{2}\sqrt{3}\)
\(\sin{240^{\circ}}\) berada di kuadran III sehingga nilainya negatif
Relasi Sudut \((270^{\circ} -\: \alpha)\) dan \((270^{\circ} + \alpha)\)
\(\text{Fungsi trigonometri berubah}\)
| \((270^{\circ} -\: \alpha)\) | \((270^{\circ} + \alpha)\) |
| $$\sin (270^{\circ} -\:\alpha) = -\cos\alpha$$ | $$\sin (270^{\circ} +\:\alpha) =-\cos\alpha$$ |
| $$\cos (270^{\circ} -\:\alpha) = -\sin \alpha$$ | $$\cos (270^{\circ} +\:\alpha) = \:\sin\alpha$$ |
| $$\tan (270^{\circ} -\:\alpha) = \:\cot\alpha$$ | $$\tan (270^{\circ} +\:\alpha) = -\cot \alpha$$ |
| $$\csc (270^{\circ} -\:\alpha) = -\sec \alpha$$ | $$\csc (270^{\circ} +\:\alpha) = -\sec \alpha$$ |
| $$\sec (270^{\circ} -\:\alpha) = -\csc \alpha$$ | $$\sec (270^{\circ} +\:\alpha) = \:\csc\alpha$$ |
| $$\cot (270^{\circ} -\:\alpha) = \:\tan\alpha$$ | $$\cot (270^{\circ} +\:\alpha) = -\tan\alpha$$ |
Contoh:
- \(\sin{240^{\circ}} = \sin{(270^{\circ} – 30^{\circ})} = -\cos 30^{\circ} = -\dfrac{1}{2}\sqrt{3}\)
\(\sin{240^{\circ}}\) berada di kuadran III sehingga nilainya negatif
- \(\cos{240^{\circ}} = \cos{(270^{\circ} – 30^{\circ})} = -\sin 30^{\circ} = -\dfrac{1}{2}\)
\(\cos{240^{\circ}}\) berada di kuadran III sehingga nilainya negatif
- \(\sec{225^{\circ}} = \sec{(270^{\circ} – 45^{\circ})} = -\csc 45^{\circ} = -\sqrt{2}\)
\(\sec{225^{\circ}}\) berada di kuadran III sehingga nilainya negatif
- \(\tan{300^{\circ}} = \tan{(270^{\circ} + 30^{\circ})} = -\cot 30^{\circ} = -\sqrt{3}\)
\(\tan{300^{\circ}}\) berada di kuadran IV sehingga nilainya negatif
- \(\csc{315^{\circ}} = \csc{(270^{\circ} + 45^{\circ})} = -\sec 45^{\circ} = -\sqrt{2}\)
\(\csc{315^{\circ}}\) berada di kuadran IV sehingga nilainya negatif
- \(\cos{330^{\circ}} = \cos{(270^{\circ} + 60^{\circ})} = +\sin 60^{\circ} = +\dfrac{1}{2}\sqrt{3}\)
\(\cos{330^{\circ}}\) berada di kuadran IV sehingga nilainya positif
Relasi Sudut \((360^{\circ} -\: \alpha)\)
\(\text{Fungsi trigonometri tetap}\)
| \((360^{\circ} -\: \alpha)\) |
| $$\sin (360^{\circ} -\:\alpha) = -\sin\alpha$$ |
| $$\cos (360^{\circ} -\:\alpha) = \:\cos \alpha$$ |
| $$\tan (360^{\circ} -\:\alpha) = -\tan\alpha$$ |
| $$\csc (360^{\circ} -\:\alpha) = -\csc\alpha$$ |
| $$\sec (360^{\circ} -\:\alpha) = \:\sec \alpha$$ |
| $$\cot (360^{\circ} -\:\alpha) = -\cot\alpha$$ |
Contoh:
- \(\sec{300^{\circ}} = \sec{(360^{\circ} – 60^{\circ})} = +\sec 60^{\circ} = +2\)
\(\sec{300^{\circ}}\) berada di kuadran IV sehingga nilainya positif
- \(\sin{330^{\circ}} = \sin{(360^{\circ} – 30^{\circ})} = -\sin 30^{\circ} = -\dfrac{1}{2}\)
\(\sin{330^{\circ}}\) berada di kuadran IV sehingga nilainya negatif
- \(\tan{315^{\circ}} = \tan{(360^{\circ} – 45^{\circ})} = -\tan 45^{\circ} = -1\)
\(\tan{315^{\circ}}\) berada di kuadran IV sehingga nilainya negatif
CONTOH SOAL
Soal 1
Tentukan nilai dari \(\dfrac{\sin 150^{\circ} + \cos 300^{\circ}}{\cos 360^{\circ} + \tan 225^{\circ}}\)
\(\dfrac{\sin 30^{\circ} + \cos 60^{\circ}}{\cos 0^{\circ} + \tan 45^{\circ}}\)
\(\dfrac{\frac{1}{2} + \frac{1}{2}}{1 + 1}\)
\(\dfrac{1}{2}\)
Soal 2
Tentukan nilai dari \(\dfrac{\sin 210^{\circ}\cdot \cos 180^{\circ}\:-\:\sin 330^{\circ}\cdot \cos 240^{\circ}}{\tan 300^{\circ}}\)
\(\dfrac{(-\sin 30^{\circ})\cdot (-\cos 0^{\circ})\:-\:(-\sin 30^{\circ})\cdot (-\cos 60^{\circ})}{-\tan 60^{\circ}}\)
\(\dfrac{(-\frac{1}{2})\cdot (-1)\:-\:(-\frac{1}{2})\cdot (-\frac{1}{2})}{-\sqrt{3}}\)
\(\dfrac{\frac{1}{2}\:-\:\frac{1}{4}}{-\sqrt{3}}\)
\(\dfrac{\frac{1}{4}}{-\sqrt{3}}\)
\(-\dfrac{1}{4\sqrt{3}}\times \color{red}\dfrac{\sqrt{3}}{\sqrt{3}}\)
\(-\dfrac{\sqrt{3}}{12}\)
Soal 3
Manakah pernyataan di bawah ini yang benar?
(1) \(\sin (90^{\circ} + \theta) = -\sin \theta\)
(2) \(\cos (270^{\circ}\:-\:\theta) = \sin \theta\)
(3) \(\cos (360^{\circ}\:-\:\theta) = \cos \theta\)
(4) \(\tan (180^{\circ} + \theta) = -\tan \theta\)
(5) \(\sec (90^{\circ} + \theta) = -\cos \theta\)
Pernyataan 1: salah
Seharusnya \(\sin (90^{\circ} + \theta) = \cos \theta\)
Pernyataan 2: salah
Seharusnya \(\cos (270^{\circ}\:-\:\theta) = -\sin \theta\)
Pernyataan 3: benar
\(\cos (360^{\circ}\:-\:\theta) = \cos \theta\)
Pernyataan 4: salah
Seharusnya \(\tan (180^{\circ} + \theta) = \tan \theta\)
Pernyataan 5: salah
Seharusnya \(\sec (90^{\circ} + \theta) = -\csc \theta\)
Soal 4
Tentukan bentuk sederhana dari \(\dfrac{\sin (\frac{1}{2}\pi\:-\:x)\cdot \cos (\frac{3}{2}\pi\:-\:x)}{\cos (2\pi\:-\:x)}\)
\(\dfrac{\sin (90^{\circ}\:-\:x)\cdot \cos (270^{\circ}\:-\:x)}{\cos (360^{\circ}\:-\:x)}\)
\(\dfrac{\cancel{\cos x} \cdot (-\sin x)}{\cancel{\cos x}}\)
\(-\sin x\)
Soal 5
Diketahui \(\sin \theta = -\dfrac{7}{25}\), dengan \(270^{\circ} < \theta < 360^{\circ}\). Tentukan nilai dari \(\sec \theta + \tan \theta\)
\(\theta\) berada di kuadran ke IV, sehingga nilai \(\sin \theta\) negatif.
Membuat segitiga siku-siku yang memenuhi \(\sin \theta = -\dfrac{7}{25}\).
Tanda negatif tidak diikutkan dalam gambar.

Sisi samping (x) dapat dihitung menggunakan rumus pythagoras
\(x^2 + 7^2 = 25^2\)
\(x^2 + 49 = 625\)
\(x^2 = 625\:-\:49\)
\(x^2 = 576\)
\(x = \sqrt{576} = 24\)
\(\sec \theta + \tan \theta = \frac{25}{24} \:-\:\frac{7}{24}\)
\(\sec \theta + \tan \theta = \frac{18}{24} = \frac{3}{4}\)
