Quiz-summary
0 of 8 questions completed
Pertanyaan:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
Information
Dear Students,
Welcome to today’s quiz! This is your opportunity to demonstrate what you’ve learned so far, so do your best. Please keep in mind that you have a maximum of 60 minutes to complete all the questions. Make sure to manage your time wisely and answer each question thoughtfully.
Good luck!
Anda telah menyelesaikan kuis sebelumnya. Oleh karena itu, Anda tidak dapat memulainya lagi.
Quiz is loading...
You must sign in or sign up to start the quiz.
You have to finish following quiz, to start this quiz:
Hasil
0 dari 8 pertanyaan terjawab dengan benar
Waktu Anda:
Time has elapsed
Anda telah meraih 0 dari 0 poin, (0)
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- Dijawab
- Ragu-Ragu
-
Pertanyaan 1 dari 8
1. Pertanyaan
1 pointsDiketahui persamaan sebuah elips adalah \(9x^2 + 16y^2 = 576\)
Terdapat beberapa pernyataan mengenai elips tersebut.
(1) Merupakan elips horizontal dan berpusat di titik (0, 0)
(2) Panjang sumbu mayornya 16 dan panjang sumbu minornya 12
(3) Koordinat titik fokus elips di \((-\sqrt{28}, 0)\) dan \((\sqrt{28}, 0)\)
(4) Koordinat titik puncak mayor elips di \((-6, 0)\) dan \((6, 0)\)
(5) Panjang latus rektum = 9
(6) Eksentrisitas \(e = \dfrac{\sqrt{7}}{8} \)
Pernyataan yang salah adalah nomor…
Benar
\(9x^2 + 16y^2 = 576\) bagi kedua ruas dengan 576, sehingga diperoleh persamaan elips \(\dfrac{x^2}{64} + \dfrac{y^2}{36} = 1\)
\(a = \sqrt{64} = 8\)
\(b = \sqrt{36} = 6\)
\(c^2 = a^2 \:-\:b^2\)
\(c^2 = 8^2 \:-\:6^2\)
\(c^2 = 64\:-\:36\)
\(c = \sqrt{28}\)
\(c = 2\sqrt{7}\)
Elips tersebut merupakan elips horizontal yang berpusat di titik (0, 0)
Panjang sumbu mayor = \(2a = 16\)
Panjang sumbu minor = \(2b = 12\)
Koordinat titik fokus elips \((-c, 0)\) dan \((c, 0)\) yakni berada di titik \((-2\sqrt{7}, 0)\) dan \((2\sqrt{7}, 0)\)
Koordinat titik puncak mayor elips \((-a, 0)\) dan \((a, 0)\) yakni berada di titik \((-8, 0)\) dan \((8, 0)\)
Panjang latus rektum = \(\dfrac{2b^2}{a} = \dfrac{2\cdot 6^2}{8} = 9\)
Eksentrisitas \(e = \dfrac{c}{a} = \dfrac{2\sqrt{7}}{8} = \dfrac{\sqrt{7}}{4} \)
Salah
\(9x^2 + 16y^2 = 576\) bagi kedua ruas dengan 576, sehingga diperoleh persamaan elips \(\dfrac{x^2}{64} + \dfrac{y^2}{36} = 1\)
\(a = \sqrt{64} = 8\)
\(b = \sqrt{36} = 6\)
\(c^2 = a^2 \:-\:b^2\)
\(c^2 = 8^2 \:-\:6^2\)
\(c^2 = 64\:-\:36\)
\(c = \sqrt{28}\)
\(c = 2\sqrt{7}\)
Elips tersebut merupakan elips horizontal yang berpusat di titik (0, 0)
Panjang sumbu mayor = \(2a = 16\)
Panjang sumbu minor = \(2b = 12\)
Koordinat titik fokus elips \((-c, 0)\) dan \((c, 0)\) yakni berada di titik \((-2\sqrt{7}, 0)\) dan \((2\sqrt{7}, 0)\)
Koordinat titik puncak mayor elips \((-a, 0)\) dan \((a, 0)\) yakni berada di titik \((-8, 0)\) dan \((8, 0)\)
Panjang latus rektum = \(\dfrac{2b^2}{a} = \dfrac{2\cdot 6^2}{8} = 9\)
Eksentrisitas \(e = \dfrac{c}{a} = \dfrac{2\sqrt{7}}{8} = \dfrac{\sqrt{7}}{4} \)
-
Pertanyaan 2 dari 8
2. Pertanyaan
1 pointsDiketahui persamaan sebuah elips adalah \(64x^2 + 25y^2 = 1.600\)
Terdapat beberapa pernyataan mengenai elips tersebut.
(1) Merupakan elips horizontal dan berpusat di titik (0, 0)
(2) Panjang sumbu mayornya 16 dan panjang sumbu minornya 10
(3) Koordinat titik fokus elips di \((-\sqrt{39}, 0)\) dan \((\sqrt{39}, 0)\)
(4) Koordinat titik puncak mayor elips di \((0, -8)\) dan \((0, 8)\)
(5) Panjang latus rektum = \(\dfrac{25}{2}\)
(6) Eksentrisitas \(e = \dfrac{\sqrt{39}}{8}\)
Pernyataan yang benar adalah nomor…
Benar
\(64x^2 + 25y^2 = 1.600\) bagi kedua ruas dengan 1.600 sehingga diperoleh persamaan elips \(\dfrac{x^2}{25} + \dfrac{y^2}{64} = 1\)
Ini merupakan persamaan elips vertikal yang berpusat di (0, 0)
\(a = \sqrt{64} = 8\)
\(b = \sqrt{25} = 5\)
\(c^2 = a^2 \:-\:b^2\)
\(c^2 = 8^2 \:-\:5^2\)
\(c^2 = 64\:-\:25\)
\(c = \sqrt{39}\)
Panjang sumbu mayornya = \(2a = 16\) dan panjang sumbu minornya = \(2b = 10\)
Koordinat titik fokus elips \((0, -c)\) dan \((0, c)\) yaitu di \((0, -\sqrt{39})\) dan \((0, \sqrt{39})\)
Koordinat titik puncak mayor elips di \((0, -8)\) dan \((0, 8)\)
Panjang latus rektum = \(\dfrac{2b^2}{a} = \dfrac{2 \cdot 5^2}{8} = \dfrac{25}{4}\)
Eksentrisitas \(e = \dfrac{c}{a} = \dfrac{\sqrt{39}}{8}\)
Salah
\(64x^2 + 25y^2 = 1.600\) bagi kedua ruas dengan 1.600 sehingga diperoleh persamaan elips \(\dfrac{x^2}{25} + \dfrac{y^2}{64} = 1\)
Ini merupakan persamaan elips vertikal yang berpusat di (0, 0)
\(a = \sqrt{64} = 8\)
\(b = \sqrt{25} = 5\)
\(c^2 = a^2 \:-\:b^2\)
\(c^2 = 8^2 \:-\:5^2\)
\(c^2 = 64\:-\:25\)
\(c = \sqrt{39}\)
Panjang sumbu mayornya = \(2a = 16\) dan panjang sumbu minornya = \(2b = 10\)
Koordinat titik fokus elips \((0, -c)\) dan \((0, c)\) yaitu di \((0, -\sqrt{39})\) dan \((0, \sqrt{39})\)
Koordinat titik puncak mayor elips di \((0, -8)\) dan \((0, 8)\)
Panjang latus rektum = \(\dfrac{2b^2}{a} = \dfrac{2 \cdot 5^2}{8} = \dfrac{25}{4}\)
Eksentrisitas \(e = \dfrac{c}{a} = \dfrac{\sqrt{39}}{8}\)
-
Pertanyaan 3 dari 8
3. Pertanyaan
1 pointsPernyataan yang benar untuk elips \(9x^2 + 25y^2\:-\:36x + 50y \:-\:164 = 0\) adalah…
Benar
\(9x^2 \:-\:36x +25y^2 + 50y = 164\)
\(9(x^2 \:-\:4x) +25(y^2 + 2y) = 164\)
\(9(x^2 \:-\:4x + 4)\:-\:36 +25(y^2 + 2y + 1)\:-\:25 = 164\)
\(9(x\:-\:2)^2 + 25(y + 1)^2 = 164 + 36 + 25\)
\(9(x\:-\:2)^2 + 25(y + 1)^2 = 225\)
Bagi kedua ruas dengan 225
\(\dfrac{(x\:-\:2)^2}{25} + \dfrac{(y + 1)^2}{9} = 1\)
Ini merupakan persamaan elips horizontal yang berpusat di \((2, -1)\)
\(a = \sqrt{25} = 5\)
\(b = \sqrt{9} = 3\)
\(c^2 = a^2 \:-\:b^2\)
\(c^2 = 5^2\:-\:3^2\)
\(c^2 = 16\)
\(c = \sqrt{16} = 4\)
Fokus elips \((h \pm c, k)\) yaitu berada di \((2 \:-\:4, -1)\) dan \((2 + 4, -1)\)
Fokus elips berada di \((-2, -1)\) dan \((6, -1)\)
Panjang sumbu mayor = \(2a = 10\)
Panjang latus rektum = \(\dfrac{2b^2}{a} = \dfrac{2 \cdot 3^2}{5}\)
Panjang latus rektum = \(\dfrac{18}{5}\)
Puncak mayor elips \((h \pm a, k)\) yaitu di \((2\:-\:5, -1)\) dan \((2 + 5, -1)\).
Puncak mayor elips di \((-3, -1)\) dan \((7, -1)\).
Salah
\(9x^2 \:-\:36x +25y^2 + 50y = 164\)
\(9(x^2 \:-\:4x) +25(y^2 + 2y) = 164\)
\(9(x^2 \:-\:4x + 4)\:-\:36 +25(y^2 + 2y + 1)\:-\:25 = 164\)
\(9(x\:-\:2)^2 + 25(y + 1)^2 = 164 + 36 + 25\)
\(9(x\:-\:2)^2 + 25(y + 1)^2 = 225\)
Bagi kedua ruas dengan 225
\(\dfrac{(x\:-\:2)^2}{25} + \dfrac{(y + 1)^2}{9} = 1\)
Ini merupakan persamaan elips horizontal yang berpusat di \((2, -1)\)
\(a = \sqrt{25} = 5\)
\(b = \sqrt{9} = 3\)
\(c^2 = a^2 \:-\:b^2\)
\(c^2 = 5^2\:-\:3^2\)
\(c^2 = 16\)
\(c = \sqrt{16} = 4\)
Fokus elips \((h \pm c, k)\) yaitu berada di \((2 \:-\:4, -1)\) dan \((2 + 4, -1)\)
Fokus elips berada di \((-2, -1)\) dan \((6, -1)\)
Panjang sumbu mayor = \(2a = 10\)
Panjang latus rektum = \(\dfrac{2b^2}{a} = \dfrac{2 \cdot 3^2}{5}\)
Panjang latus rektum = \(\dfrac{18}{5}\)
Puncak mayor elips \((h \pm a, k)\) yaitu di \((2\:-\:5, -1)\) dan \((2 + 5, -1)\).
Puncak mayor elips di \((-3, -1)\) dan \((7, -1)\).
-
Pertanyaan 4 dari 8
4. Pertanyaan
1 pointsPersamaan elips yang memiliki puncak mayor \((\pm9, 0)\) dan salah satu fokusnya \((7, 0)\) adalah…
Benar
Pusat elips berada di \((0, 0)\)
Fokus \((7, 0)\), maka nilai \(c = 7\)
puncak mayor \((\pm9, 0)\), maka nilai \(a = 9\)
\(c^2 = a^2 \:-\:b^2\)
\(7^2 = 9^2\:-\:b^2\)
\(49 = 81 \:-\:b^2\)
\(b^2 = 32\)
Persamaan elips \(\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1\)
\(\dfrac{x^2}{81} + \dfrac{y^2}{32} = 1\)
Salah
Pusat elips berada di \((0, 0)\)
Fokus \((7, 0)\), maka nilai \(c = 7\)
puncak mayor \((\pm9, 0)\), maka nilai \(a = 9\)
\(c^2 = a^2 \:-\:b^2\)
\(7^2 = 9^2\:-\:b^2\)
\(49 = 81 \:-\:b^2\)
\(b^2 = 32\)
Persamaan elips \(\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1\)
\(\dfrac{x^2}{81} + \dfrac{y^2}{32} = 1\)
-
Pertanyaan 5 dari 8
5. Pertanyaan
1 pointsPersamaan elips dengan puncak mayor \((-5, -1)\) dan \((11, -1)\) serta salah satu fokusnya \((-3, -1)\) adalah…
Benar
Pusat elips berada di tengah-tengah ruas garis yang menghubungkan titik puncak mayor.
Pusat = \(\left(\dfrac{x_1 + x_2}{2}, \dfrac{y_1 + y_2}{2}\right)\)
Pusat = \(\left(\dfrac{-5 + 11}{2}, \dfrac{-1 + (-1)}{2}\right)\)
Pusat = \((3, -1)\)
Jarak pusat ke salah satu puncak = \(a\)
Jarak puncak \((-5, -1)\) ke pusat \((3, -1)\) = 8
Nilai \(a = 8\)
Jarak pusat ke salah satu titik fokus = \(c\)
Jarak fokus \((-3, -1)\) ke pusat \((3, -1)\) = 6
Nilai \(c = 6\)
\(c^2 = a^2 \:-\:b^2\)
\(6^2 = 8^2 \:-\:b^2\)
\(36 = 64 \:-\:b^2\)
\(b^2 = 28\)
Persamaan elips yang berpusat di \((3, -1)\) adalah:
\(\dfrac{(x\:-\:3)^2}{64} + \dfrac{(y + 1)^2}{28} = 1\)
Salah
Pusat elips berada di tengah-tengah ruas garis yang menghubungkan titik puncak mayor.
Pusat = \(\left(\dfrac{x_1 + x_2}{2}, \dfrac{y_1 + y_2}{2}\right)\)
Pusat = \(\left(\dfrac{-5 + 11}{2}, \dfrac{-1 + (-1)}{2}\right)\)
Pusat = \((3, -1)\)
Jarak pusat ke salah satu puncak = \(a\)
Jarak puncak \((-5, -1)\) ke pusat \((3, -1)\) = 8
Nilai \(a = 8\)
Jarak pusat ke salah satu titik fokus = \(c\)
Jarak fokus \((-3, -1)\) ke pusat \((3, -1)\) = 6
Nilai \(c = 6\)
\(c^2 = a^2 \:-\:b^2\)
\(6^2 = 8^2 \:-\:b^2\)
\(36 = 64 \:-\:b^2\)
\(b^2 = 28\)
Persamaan elips yang berpusat di \((3, -1)\) adalah:
\(\dfrac{(x\:-\:3)^2}{64} + \dfrac{(y + 1)^2}{28} = 1\)
-
Pertanyaan 6 dari 8
6. Pertanyaan
1 pointsPersamaan garis singgung elips \(\dfrac{x^2}{9} + \dfrac{y^2}{8} = 1\) di titik berabsis \(1\) adalah…
Benar
Menentukan titik singgung.
\(\dfrac{1^2}{9} + \dfrac{y^2}{8} = 1\)
\( \dfrac{y^2}{8} = 1\:-\:\dfrac{1}{9}\)
\( \dfrac{y^2}{8} = \dfrac{8}{9}\)
\(y^2 = \dfrac{64}{9}\)
\(y = \pm \sqrt{\dfrac{64}{9}}\)
\(y = \pm \dfrac{8}{3}\)
Titik singgung \((1, -\dfrac{8}{3})\) dan \((1, \dfrac{8}{3})\)
Persamaan garis singgung:
\(\dfrac{x_1 \cdot x}{9} + \dfrac{y_1 \cdot y}{8} = 1\)
Persamaan garis singgung di titik \((1, -\dfrac{8}{3})\):
\(\dfrac{x}{9} + \dfrac{-\dfrac{8}{3}\cdot y}{8} = 1\)
\(\dfrac{x}{9} \:-\: \dfrac{y}{3} = 1\)
Kalikan kedua ruas dengan 9
\(x\:-\:3y = 9\)
Persamaan garis singgung di titik \((1, \dfrac{8}{3})\):
\(\dfrac{x}{9} + \dfrac{\dfrac{8}{3}\cdot y}{8} = 1\)
\(\dfrac{x}{9}+ \dfrac{y}{3} = 1\)
Kalikan kedua ruas dengan 9
\(x + 3y = 9\)
Salah
Menentukan titik singgung.
\(\dfrac{1^2}{9} + \dfrac{y^2}{8} = 1\)
\( \dfrac{y^2}{8} = 1\:-\:\dfrac{1}{9}\)
\( \dfrac{y^2}{8} = \dfrac{8}{9}\)
\(y^2 = \dfrac{64}{9}\)
\(y = \pm \sqrt{\dfrac{64}{9}}\)
\(y = \pm \dfrac{8}{3}\)
Titik singgung \((1, -\dfrac{8}{3})\) dan \((1, \dfrac{8}{3})\)
Persamaan garis singgung:
\(\dfrac{x_1 \cdot x}{9} + \dfrac{y_1 \cdot y}{8} = 1\)
Persamaan garis singgung di titik \((1, -\dfrac{8}{3})\):
\(\dfrac{x}{9} + \dfrac{-\dfrac{8}{3}\cdot y}{8} = 1\)
\(\dfrac{x}{9} \:-\: \dfrac{y}{3} = 1\)
Kalikan kedua ruas dengan 9
\(x\:-\:3y = 9\)
Persamaan garis singgung di titik \((1, \dfrac{8}{3})\):
\(\dfrac{x}{9} + \dfrac{\dfrac{8}{3}\cdot y}{8} = 1\)
\(\dfrac{x}{9}+ \dfrac{y}{3} = 1\)
Kalikan kedua ruas dengan 9
\(x + 3y = 9\)
-
Pertanyaan 7 dari 8
7. Pertanyaan
1 pointsDi Washington, D.C., terdapat taman yang dinamai The Ellipse. Taman ini terletak di antara Gedung Putih dan Monumen Washington. Taman tersebut dikelilingi oleh suatu jalan yang berbentuk elips dengan panjang sumbu mayor dan minornya berturut-turut 458 meter dan 390 meter. Apabila pengelola taman tersebut ingin membangun air mancur pada masing-masing titik fokus taman tersebut, jarak antara kedua air mancur tersebut adalah…
 Benar
Benar
Panjang sumbu mayor = \(2a = 458 \rightarrow a = 229\)
Panjang sumbu minor = \(2b = 390 \rightarrow b = 195\)
\(c^2 = a^2 \:-\:b^2\)
\(c^2 = 229^2\:-\:195^2\)
\(c^2 = (229 + 195)(229\:-\:195)\)
\(c^2 = 424 (34)\)
\(c^2 = 14.416\)
\(c = \sqrt{14.416} \approx 120\)
Jarak antara kedua air mancur tersebut adalah 2c = 2 × 120 = 240 m
Salah
Panjang sumbu mayor = \(2a = 458 \rightarrow a = 229\)
Panjang sumbu minor = \(2b = 390 \rightarrow b = 195\)
\(c^2 = a^2 \:-\:b^2\)
\(c^2 = 229^2\:-\:195^2\)
\(c^2 = (229 + 195)(229\:-\:195)\)
\(c^2 = 424 (34)\)
\(c^2 = 14.416\)
\(c = \sqrt{14.416} \approx 120\)
Jarak antara kedua air mancur tersebut adalah 2c = 2 × 120 = 240 m
-
Pertanyaan 8 dari 8
8. Pertanyaan
1 pointsLitotripsi merupakan suatu prosedur medis yang dilakukan untuk menghancurkan batu di saluran kemih dengan menggunakan gelombang kejut ultrasonik (ultrasonic shockwave) sehingga pecahannya dapat lolos dari tubuh. Alat yang dipakai adalah litotripter, berbentuk setengah elips 3 dimensi yang mengaplikasikan sifat-sifat dari titik fokus elips. Alat ini dipakai untuk mengumpulkan gelombang ultrasonik pada suatu titik fokus untuk ditembakkan ke batu ginjal yang terletak di titik fokus lainnya.
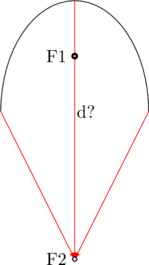
Jika litotripter tersebut memiliki panjang (sumbu semi mayor) 16 cm dan berjari-jari (sumbu semi minor) 10 cm, seberapa jauh dari titik puncak seharusnya batu ginjal tersebut diposisikan agar diperoleh hasil yang optimal?
Benar
Panjang sumbu semi mayor \(a = 16\)
Panjang sumbu semi minor \(b = 10\)
\(c^2 = a^2 \:-\:b^2\)
\(c^2 = 16^2 \:-\:10^2\)
\(c^2 = 256\:-\:100\)
\(c^2 = 156\)
\(c = \sqrt{156} = 2\sqrt{39}\)
Jarak titik puncak dengan titik fokus ke-2 adalah \(a + c = 16 + 2\sqrt{39}\)
Jadi batu ginjal tersebut diposisikan pada jarak \(16 + 2\sqrt{39}\) meter dari puncak.
Salah
Panjang sumbu semi mayor \(a = 16\)
Panjang sumbu semi minor \(b = 10\)
\(c^2 = a^2 \:-\:b^2\)
\(c^2 = 16^2 \:-\:10^2\)
\(c^2 = 256\:-\:100\)
\(c^2 = 156\)
\(c = \sqrt{156} = 2\sqrt{39}\)
Jarak titik puncak dengan titik fokus ke-2 adalah \(a + c = 16 + 2\sqrt{39}\)
Jadi batu ginjal tersebut diposisikan pada jarak \(16 + 2\sqrt{39}\) meter dari puncak.
