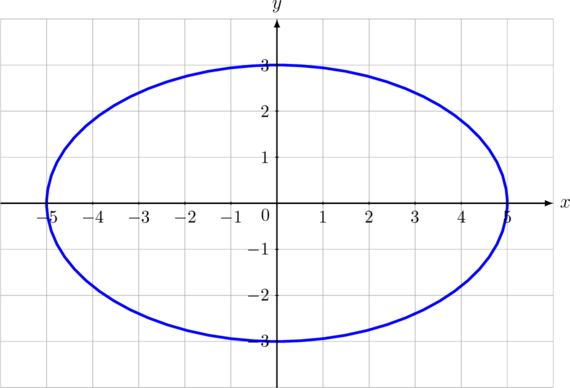
\(\dfrac{x^2}{25} + \dfrac{y^2}{9} = 1\) merupakan persamaan elips horizontal berpusat di (0, 0) dengan \(a = 5\) dan \(b = 3\)
\(c^2 = a^2 \:-\:b^2\)
\(c^2 = 5^2\:-\:3^2\)
\(c^2 = 9\)
\(c = \sqrt{9} = 3\)
(A) Pusat = (0, 0)
(B) Fokus di \((-3, 0) \text{ dan } (3, 0)\)
(C) Puncak mayor di: \((-5, 0) \text{ dan } (5, 0)\)
(D) Panjang sumbu mayor = \(2a = 10\)
(E) Panjang sumbu minor = \(2b = 6\)
(F) Eksentrisitas \(e = \dfrac{c}{a} = \dfrac{3}{5}\)
(G) Persamaan direktris \(x = -\dfrac{a^2}{c} = -\dfrac{25}{3} \text{ dan } x =\dfrac{a^2}{c} = \dfrac{25}{3}\)
(H) Panjang latus rektum = \(\dfrac{2b^2}{a} = \dfrac{18}{5}\)
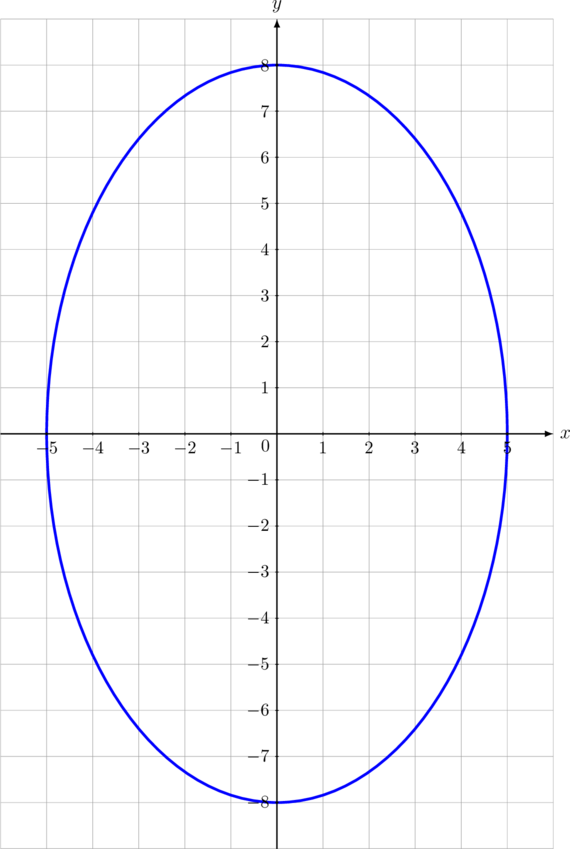
\(\dfrac{x^2}{25} + \dfrac{y^2}{64} = 1\) merupakan persamaan elips vertikal berpusat di (0, 0) dengan \(a = 8\) dan \(b = 5\)
\(c^2 = a^2 \:-\:b^2\)
\(c^2 = 8^2\:-\:5^2\)
\(c^2 = 39\)
\(c = \sqrt{39}\)
(A) Pusat = (0, 0)
(B) Fokus di \((0, -\sqrt{39}) \text{ dan } (0, \sqrt{39})\)
(C) Puncak di: \((0, -8) \text{ dan } (0, 8)\), \((-5, 0) \text{ dan } (5, 0)\)
(D) Panjang sumbu mayor = \(2a = 16\)
(E) Panjang sumbu minor = \(2b = 10\)
(F) Eksentrisitas \(e = \dfrac{c}{a} = \dfrac{\sqrt{39}}{8}\)
(G) Persamaan direktris \(y = -\dfrac{a^2}{c} = -\dfrac{64}{\sqrt{39}} \text{ dan } y =\dfrac{a^2}{c} = \dfrac{64}{\sqrt{39}}\)
(H) Panjang latus rektum = \(\dfrac{2b^2}{a} = \dfrac{50}{8}\)
Tuliskan persamaan elips berikut dalam bentuk standar, kemudian tentukan pusat dan koordinat titik fokusnya.
(A) \(\color{blue} 9x^2 + y^2 + 54x \:-\:4y + 76 = 0\)
\(9x^2 + 54x + y^2 \:-\:4y = -76\)
\(9(x^2 + 6x + 9)\:-\:81 + (y^2 \:-\:4y + 4) \:-\:4 = -76\)
\(9(x^2 + 6x + 9) + (y^2 \:-\:4y + 4) = -76 + 81 + 4\)
\(9(x^2 + 6x + 9) + (y^2 \:-\:4y + 4) = 9\)
\(9(x + 3)^2 + (y\:-\:2)^2 = 9\)
Bagi kedua ruas dengan 9
Persamaan elips:
\(\dfrac{(x + 3)^2}{1} + \dfrac{(y\:-\:2)^2}{9} = 1\)
Ini merupakan persamaan elips vertikal yang berpusat di \((-3, 2)\)
\(a = 3\) dan \(b = 1\)
\(c^2 = a^2 \:-\:b^2\)
\(c^2 = 3^2\:-\:1^2\)
\(c^2 = 8\)
\(c =\sqrt{8} = 2\sqrt{2}\)
Koordinat titik fokus \(\color{blue} (h, k \pm c)\)
\((-3, 2 + 2\sqrt{2})\) dan \((-3, 2 \:-\: 2\sqrt{2})\)
(B) \(\color{blue} 9x^2 + 36y^2\:-\:36x + 72y + 36 = 0\)
\(9x^2 + 36y^2\:-\:36x + 72y + 36 = 0\)
\(9x^2\:-\:36x + 36y^2 + 72y = -36\)
\(9(x^2 \:-\:4x + 4) \:-\: 36 + 36(y^2 + 2y + 1)\:-\:36 = -36\)
\(9(x\:-\:2)^2 + 36(y + 1)^2 = -36 + 36 + 36\)
\(9(x\:-\:2)^2 + 36(y + 1)^2 = 36\)
Bagi kedua ruas dengan 36
Persamaan elips:
\(\dfrac{(x\:-\:2)^2}{4} + \dfrac{(y + 1)^2}{1} = 1\)
Ini merupakan persamaan elips horizontal yang berpusat di \((2, -1)\)
\(a = 2\) dan \(b = 1\)
\(c^2 = a^2 \:-\:b^2\)
\(c^2 = 2^2\:-\:1^2\)
\(c^2 = 3\)
\(c =\sqrt{3}\)
Koordinat titik fokus \(\color{blue} (h \pm c, k)\)
\((2 + \sqrt{3}, -1)\) dan \((2\:-\:\sqrt{3}, -1)\)
\(x^2 + 4y^2 \:-\:4x \:-\:8y = 92\)
\(x^2 \:-\:4x + 4y^2 \:-\:8y = 92\)
\((x^2 \:-\:4x + 4)\:-\:4 + 4(y^2\:-\:2y + 1)\:-\:4 = 92\)
\((x\:-\:2)^2 + 4(y\:-\:1)^2 = 92 + 4 + 4\)
\((x\:-\:2)^2 + 4(y\:-\:1)^2 = 100\)
Bagi kedua ruas dengan 100
Persamaan elips:
\(\dfrac{(x\:-\:2)^2}{100} + \dfrac{(y\:-\:1)^2}{25} = 1\)
Ini adalah persamaan elips horizontal yang berpusat di \((2, 1)\)
\(a = 10\) dan \(b = 5\)
\(c^2 = a^2 \:-\:b^2\)
\(c^2 = 10^2\:-\:5^2\)
\(c^2 = 75\)
\(c = \sqrt{75} = 5\sqrt{3}\)
(A) Pusat = (2, 1)
(B) Fokus = \((2 + 5\sqrt{3}, 1)\) dan \((2\:-\:5\sqrt{3}, 1)\)
(C) Puncak =\((2 \pm 10, 1)\) dan \((2, 1 \pm 5)\)
(D) Panjang sumbu mayor = \(2a = 20\)
(E) Panjang sumbu minor = \(2b = 10\)
(F) Eksentrisitas \(e = \dfrac{c}{a} = \dfrac{5\sqrt{3}}{10}\)
(G) Persamaan direktris \(x = -\dfrac{a^2}{c} + h = -\dfrac{100}{5\sqrt{3}} + 2\) dan \(x = \dfrac{a^2}{c} + h = \dfrac{100}{5\sqrt{3}} + 2\)
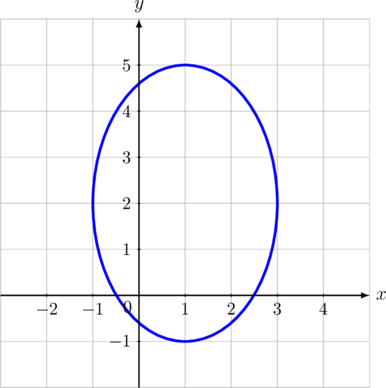
Pusat ellips di titik \((h, k) = (1, 2)\)
Panjang sumbu mayor \(2a = 6\) maka \(a = 3\)
Panjang sumbu minor \(2b = 4\) maka \(b = 2\)
Persamaan ellips vertikal:
\(\color{blue} \dfrac{(x\:-\:h)^2}{b^2} + \dfrac{(y\:-\:k)^2}{a^2} = 1\)
\(\dfrac{(x\:-\:1)^2}{2^2} + \dfrac{(y\:-\:2)^2}{3^2} = 1\)
\(\dfrac{(x\:-\:1)^2}{4} + \dfrac{(y\:-\:2)^2}{9} = 1\)
