Soal 01
Tentukan persamaan elips yang memiliki fokus di \((6 + 2\sqrt{10}, 1)\) dan \((6 \:-\: 2\sqrt{10}, 1)\) dan panjang latus rektum \(\dfrac{18}{7}\)
Elips yang memiliki fokus di \((6 + 2\sqrt{10}, 1)\) dan \((6 \:-\: 2\sqrt{10}, 1)\) adalah elips horizontal dengan pusat di \((6, 1\)) dan \(c = 2\sqrt{10}\)
Terdapat hubungan \(c^2 = a^2 \:-\:b^2\)
\((2\sqrt{10})^2 = a^2 \:-\:b^2\)
\(b^2 = a^2\:-\:40 \dotso \color{red} (1)\)
Panjang laktus rektum = \(\dfrac{2b^2}{a}\)
\(\dfrac{18}{7} = \dfrac{2b^2}{a}\dotso \color{red} (2)\)
Substitusi persamaan (1) ke persamaan (2)
\(\dfrac{18}{7} = \dfrac{2(a^2\:-\:40)}{a}\)
Kali silang,
\(18a = 14(a^2\:-\:40)\)
\(18a = 14a^2 \:-\:560\)
\(14a^2\:-\:18a\:-\:560 = 0\)
Bagi kedua ruas dengan 2
\(7a^2 \:-\:9a\:-\:280= 0\)
\((7a + 40)(a\:-\:7) = 0\)
\(a\:-\:7 = 0 \rightarrow a = 7\)
\(b^2 = a^2\:-\:40\)
\(b^2 = 7^2\:-\:40\)
\(b^2 = 9\)
\(b = \sqrt{9} = 3\)
Persamaan elips horizontal yang berpusat di \((6, 1\)) dengan nilai \(a = 7\) dan \(b = 3\) adalah:
\(\dfrac{(x\:-\:6)^2}{7^2} + \dfrac{(y\:-\:1)^2}{3^2} = 1\)
\(\dfrac{(x\:-\:6)^2}{49} + \dfrac{(y\:-\:1)^2}{9} = 1\)
Soal 02
Tentukan persamaan elips yang berpusat di \((2, -3)\), salah satu puncak mayor di \((6, -3)\), dan salah satu fokus di \((2 + 2\sqrt{3}, -3)\).
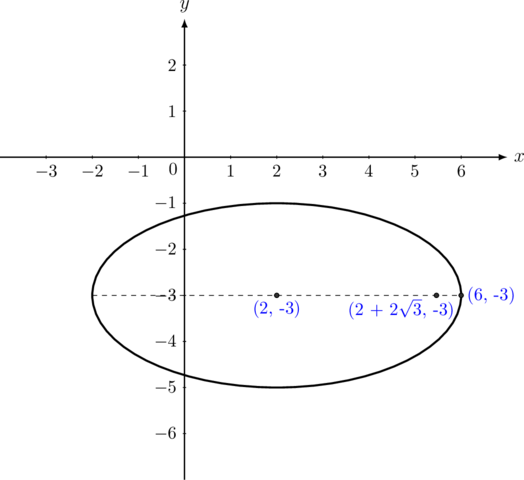
Dari gambar dapat diperoleh informasi sebagai berikut:
\(c = \text{ jarak titik pusat ke titik fokus } = 2\sqrt{3}\)
\(a = \text{ jarak titik pusat ke titik puncak } = 6\:-\:2 = 4\)
\(c^2 = a^2 \:-\:b^2\)
\((2\sqrt{3})^2 = 4^2 \:-\:b^2\)
\(12 = 16\:-\:b^2\)
\(b^2 = 4\)
\(b = \sqrt{4} = 2\)
Persamaan elips berpusat di \((2, -3)\) dan memiliki nilai \(a = 4\) dan \(b = 2\) adalah:
\(\dfrac{(x\:-\:2)^2}{4^2} + \dfrac{(y + 3)^2}{2^2} = 1\)
\(\dfrac{(x\:-\:2)^2}{16} + \dfrac{(y + 3)^2}{4} = 1\)
Soal 03
Tentukan persamaan dan titik fokus elips di bawah ini:
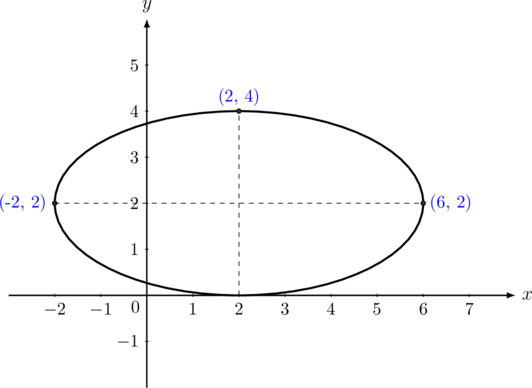
Pusat elips = \((2, 2)\)
Panjang sumbu mayor = 8
\(2a = 8 \rightarrow a = 4\)
Panjang sumbu minor = 4
\(2b = 4 \rightarrow b = 2\)
\(c^2 = a^2\:-\:b^2\)
\(c^2 = 4^2\:-\:2^2\)
\(c^2 = 12\)
\(c = \sqrt{12} = 2\sqrt{3}\)
Persamaan elips horizontal:
\(\color{blue}\dfrac{(x\:-\:h)^2}{a^2} + \dfrac{(y\:-\:k)^2}{b^2} = 1\)
\(\dfrac{(x\:-\:2)^2}{4^2} + \dfrac{(y\:-\:2)^2}{2^2} = 1\)
\(\dfrac{(x\:-\:2)^2}{16} + \dfrac{(y\:-\:2)^2}{4} = 1\)
Titik fokus \(\color{blue} (h \pm c, k)\)
\((2 + 2\sqrt{3}, 2 )\) dan \((2 \:-\: 2\sqrt{3}, 2 )\)
Soal 04
Tentukan persamaan elips yang memiliki koordinat titik puncak mayor di titik \((-1, -9)\) dan \((-1, -11)\) dan memiliki nilai eksentrisitas 0,8.
Panjang sumbu mayor = \(-9\:-\:(-11) = 2\)
\(2a = 2 \rightarrow a = 1\)
\(e = \dfrac{c}{a}\)
\(0,8 = \dfrac{c}{1}\)
\(c = 0,8\)
\(c^2 = a^2 \:-\:b^2\)
\((0,8)^2 = 1^2 \:-\:b^2\)
\(0,64 = 1 \:-\:b^2\)
\(b^2 = 0,36\)
\(b = \sqrt{0,36} = 0,6\)
Persamaan elips vertikal berpusat di \((-1, -10)\) adalah:
\(\color{blue} \dfrac{(x\:-\:h)^2}{b^2} + \dfrac{(y\:-\:k)^2}{a^2} = 1\)
\(\dfrac{(x + 1)^2}{(0,6)^2} + \dfrac{(y + 10)^2}{1^2} = 1\)
\(\dfrac{(x + 1)^2}{0,36} + \dfrac{(y + 10)^2}{1} = 1\)
Soal 05
Tentukan persamaan garis singgung elips \(\dfrac{x^2}{40} + \dfrac{y^2}{20} = 1\) di titik berabsis \(\sqrt{22}\)
Langkah 1: menentukan titik singgung
Substitusikan \(x = \sqrt{22}\) ke persamaan elips
\(\dfrac{(\sqrt{22})^2}{40} + \dfrac{y^2}{20} = 1\)
\(\dfrac{22}{40} + \dfrac{y^2}{20} = 1\)
\(\dfrac{y^2}{20} = 1 \:-\:\dfrac{22}{40}\)
\(\dfrac{y^2}{20} = \dfrac{18}{40}\)
\(y^2 = 9\)
\(y = \pm \sqrt{9} = \pm 3\)
Titik singgungnya berada di \((\sqrt{22}, -3)\) dan \((\sqrt{22}, 3)\)
Langkah 2: menentukan persamaan garis singgung
Persamaan garis singgung di titik \((\sqrt{22}, -3)\):
\(\dfrac{x_1 \cdot x}{a^2} + \dfrac{y_1 \cdot y}{b^2} = 1\)
\(\dfrac{\sqrt{22} \cdot x}{40} + \dfrac{-3\cdot y}{20} = 1\)
Kalikan kedua ruas dengan 40
\(\sqrt{22} \cdot x \:-\:6 \cdot y = 40\)
\(\color{blue} \sqrt{22}x\:-\:6y\:-\:40 = 0\)
Persamaan garis singgung di titik \((\sqrt{22}, 3)\):
\(\dfrac{x_1 \cdot x}{a^2} + \dfrac{y_1 \cdot y}{b^2} = 1\)
\(\dfrac{\sqrt{22} \cdot x}{40} + \dfrac{3\cdot y}{20} = 1\)
Kalikan kedua ruas dengan 40
\(\sqrt{22} \cdot x + 6 \cdot y = 40\)
\(\color{blue} \sqrt{22}x + 6y\:-\:40 = 0\)
Soal 06
Tentukan persamaan garis singgung elips \(5x^2 + 9y^2\:-\:10x + 36y \:-\:4 = 0\) yang tegak lurus garis \(3x + 2y + 1 = 0\)
\(5x^2 \:-\:10x + 9y^2 + 36y = 4\)
\(5(x^2\:-\:2x + 1)\:-\:5 + 9(y^2 + 4y + 4)\:-\:36 = 4\)
\(5(x^2\:-\:2x + 1) + 9(y^2 + 4y + 4) = 4 + 5 + 36\)
\(5(x^2\:-\:2x + 1) + 9(y^2 + 4y + 4) = 45\)
\(5(x\:-\:1)^2 + 9(y + 2)^2 = 45\)
Bagi kedua ruas dengan 45
\(\dfrac{(x\:-\:1)^2}{9} + \dfrac{(y + 2)^2}{5} = 1\)
Pusat elips horizontal \((1, -2)\)
\(a = 3\) dan \(b = \sqrt{5}\)
Menentukan gradien garis \(3x + 2y + 1 = 0\)
\(2y = -3x\:-\:1\)
\(y = -\dfrac{3}{2}x\:-\:\dfrac{1}{2}\)
\(m_1 = -\dfrac{3}{2}\)
Menentukan gradien garis singgung elips \(m_2\)
Garis singgung elips tegak lurus dengan garis \(3x + 2y + 1 = 0\)
\(m_1 \cdot m_2 = -1\)
\(-\dfrac{3}{2} \cdot m_2 = -1\)
\(m_2 = \dfrac{2}{3}\)
Persamaan garis singgung elips horizontal yang berpusat di \((1, -2)\) dan bergradien \(\dfrac{2}{3}\) adalah:
\(\color{blue} y\:-\:k=m(x\:-\:h) \pm \sqrt{a^2m^2 + b^2}\)
\(y + 2 =\dfrac{2}{3}(x\:-\:1) \pm \sqrt{3^2\left(\dfrac{2}{3}\right)^2 + (\sqrt{5})^2}\)
\(y + 2 =\dfrac{2}{3}(x\:-\:1) \pm \sqrt{4 + 5}\)
\(y + 2 =\dfrac{2}{3}(x\:-\:1) \pm 3\)
Kalikan kedua ruas dengan 3
\(3y + 6 = 2(x\:-\:1) \pm 9\)
\(3y + 6 = 2x \:-\:2 \pm 9\)
\(3y\:-\:2x + 6 + 2 \pm 9 = 0\)
\(3y \:-\:2x + 17 = 0\) dan \(3y \:-\:2x \:-\:1 = 0\)
