Quiz-summary
0 of 20 questions completed
Pertanyaan:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
Information
Dear Students,
Welcome to today’s quiz! This is your opportunity to demonstrate what you’ve learned so far, so do your best. Please keep in mind that you have a maximum of 60 minutes to complete all the questions. Make sure to manage your time wisely and answer each question thoughtfully.
Good luck!
Anda telah menyelesaikan kuis sebelumnya. Oleh karena itu, Anda tidak dapat memulainya lagi.
Quiz is loading...
You must sign in or sign up to start the quiz.
You have to finish following quiz, to start this quiz:
Hasil
0 dari 20 pertanyaan terjawab dengan benar
Waktu Anda:
Time has elapsed
Anda telah meraih 0 dari 0 poin, (0)
Categories
- Not categorized 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- Dijawab
- Ragu-Ragu
-
Pertanyaan 1 dari 20
1. Pertanyaan
1 pointsPersamaan garis \(x + 2y\:-\:8 = 0\) melalui titik…
Benar
Persamaan garis \(x + 2y\:-\:8 = 0\) melalui titik (2, 3) karena \(2 + 2(3) \:-\:8 = 0\)
Salah
Persamaan garis \(x + 2y\:-\:8 = 0\) melalui titik (2, 3) karena \(2 + 2(3) \:-\:8 = 0\)
-
Pertanyaan 2 dari 20
2. Pertanyaan
1 pointsGradien garis \(4x\:-\:y + 5 = 0\) adalah…
Benar
\(4x\:-\:y + 5 = 0\)
\(y = \color{red} 4\color{black} x + 5\)
Gradien garis \(4x\:-\:y + 5 = 0\) adalah \(4\)
Salah
\(4x\:-\:y + 5 = 0\)
\(y = \color{red} 4\color{black} x + 5\)
Gradien garis \(4x\:-\:y + 5 = 0\) adalah \(4\)
-
Pertanyaan 3 dari 20
3. Pertanyaan
1 pointsGaris \(x + y\:-\:10 = 0\) memotong sumbu X di titik…
Benar
Garis \(x + y\:-\:10 = 0\) memotong sumbu X, jika \(y = 0\).
\(x + 0 \:-\:10 = 0\)
\(x = 10\)
Jadi, titik potong garis \(x + y \:-\:10\) terhadap sumbu X adalah \((10, 0)\).
Salah
Garis \(x + y\:-\:10 = 0\) memotong sumbu X, jika \(y = 0\).
\(x + 0 \:-\:10 = 0\)
\(x = 10\)
Jadi, titik potong garis \(x + y \:-\:10\) terhadap sumbu X adalah \((10, 0)\).
-
Pertanyaan 4 dari 20
4. Pertanyaan
1 pointsGaris \(2y + 7x = 4\) memotong sumbu Y di titik…
Benar
Garis \(2y + 7x = 4\) memotong sumbu Y, jika \(x = 0\)
\(2y + 7(0) = 4\)
\(2y = 4\)
\(y = \dfrac{4}{2} = 2\)
Jadi, titik potong garis \(2y + 7x = 4\) terhadap sumbu Y adalah \((0, 2)\).
Salah
Garis \(2y + 7x = 4\) memotong sumbu Y, jika \(x = 0\)
\(2y + 7(0) = 4\)
\(2y = 4\)
\(y = \dfrac{4}{2} = 2\)
Jadi, titik potong garis \(2y + 7x = 4\) terhadap sumbu Y adalah \((0, 2)\).
-
Pertanyaan 5 dari 20
5. Pertanyaan
1 pointsPersamaan garis melalui titik \((-3, 4)\) dan bergradien \(-4\) adalah…
Benar
Persamaan garis melalui titik \((x_1, y_1)\) dan bergradien \(m\) adalah \(\color{blue} y\:-\:y_1 = m(x\:-\:x_1)\)
Persamaan garis melalui titik \((-3, 4)\) dan bergradien \(-4\) adalah:
\(y\:-\:4 = -4(x\:-\:(-3))\)
\(y\:-\:4 = -4(x + 3)\)
\(y\:-\:4 = -4x\:-\:12\)
\(y = -4x\:-\:12 + 4\)
\(y = -4x \:-\:8\)
\(y + 4x + 8 = 0\)
Salah
Persamaan garis melalui titik \((x_1, y_1)\) dan bergradien \(m\) adalah \(\color{blue} y\:-\:y_1 = m(x\:-\:x_1)\)
Persamaan garis melalui titik \((-3, 4)\) dan bergradien \(-4\) adalah:
\(y\:-\:4 = -4(x\:-\:(-3))\)
\(y\:-\:4 = -4(x + 3)\)
\(y\:-\:4 = -4x\:-\:12\)
\(y = -4x\:-\:12 + 4\)
\(y = -4x \:-\:8\)
\(y + 4x + 8 = 0\)
-
Pertanyaan 6 dari 20
6. Pertanyaan
1 pointsPersamaan garis yang melalui titik \((2, -5)\) dan \((-3, 0)\) adalah…
Benar
Persamaan garis yang melalui titik \((x_1, y_1)\) dan \((x_2, y_2)\) adalah \(\color{blue} \dfrac{y\:-\:y_1}{y_2 \:-\:y_1} = \dfrac{x\:-\:x_1}{x_2\:-\:x_1}\)
Persamaan garis yang melalui titik \((2, -5)\) dan \((-3, 0)\) adalah:
\(\dfrac{y\:-\:(-5)}{0 \:-\:(-5)} = \dfrac{x\:-\:2}{-3\:-\:2}\)
\(\dfrac{y + 5}{5} = \dfrac{x\:-\:2}{-5}\)
Kalikan kedua ruas dengan 5
\(y + 5 = -(x\:-\:2)\)
\(y + 5 = -x + 2\)
\(y = -x + 2\:-\:5\)
\(y = -x \:-\:3\)
\(x + y + 3 = 0\)
Salah
Persamaan garis yang melalui titik \((x_1, y_1)\) dan \((x_2, y_2)\) adalah \(\color{blue} \dfrac{y\:-\:y_1}{y_2 \:-\:y_1} = \dfrac{x\:-\:x_1}{x_2\:-\:x_1}\)
Persamaan garis yang melalui titik \((2, -5)\) dan \((-3, 0)\) adalah:
\(\dfrac{y\:-\:(-5)}{0 \:-\:(-5)} = \dfrac{x\:-\:2}{-3\:-\:2}\)
\(\dfrac{y + 5}{5} = \dfrac{x\:-\:2}{-5}\)
Kalikan kedua ruas dengan 5
\(y + 5 = -(x\:-\:2)\)
\(y + 5 = -x + 2\)
\(y = -x + 2\:-\:5\)
\(y = -x \:-\:3\)
\(x + y + 3 = 0\)
-
Pertanyaan 7 dari 20
7. Pertanyaan
1 pointsGradien garis yang melalui titik \((-1, 10)\) dan \((1, 12)\) adalah…
Benar
Gradien garis yang melalui titik \((x_1, y_1)\) dan \((x_2, y_2)\) adalah \(m = \dfrac{y_2\:-\:y_1}{x_2\:-\:x_1}\)
Gradien garis yang melalui titik \((-1, 10)\) dan \((1, 12)\) adalah:
\(m = \dfrac{12\:-\:10}{1\:-\:(-1)}\)
\(m = \dfrac{2}{2}\)
\(m = 1\)
Salah
Gradien garis yang melalui titik \((x_1, y_1)\) dan \((x_2, y_2)\) adalah \(m = \dfrac{y_2\:-\:y_1}{x_2\:-\:x_1}\)
Gradien garis yang melalui titik \((-1, 10)\) dan \((1, 12)\) adalah:
\(m = \dfrac{12\:-\:10}{1\:-\:(-1)}\)
\(m = \dfrac{2}{2}\)
\(m = 1\)
-
Pertanyaan 8 dari 20
8. Pertanyaan
1 points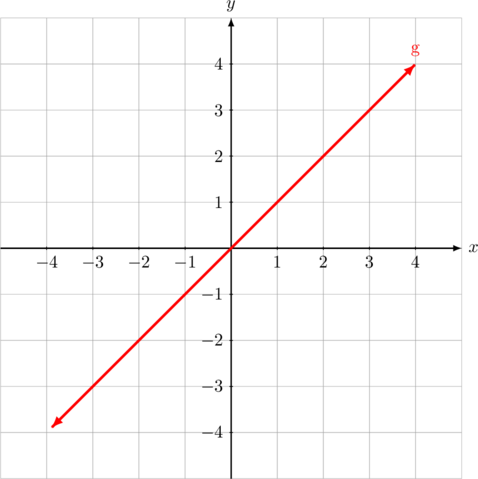
Persamaan garis \(g\) adalah…
Benar
garis \(g\) melalui titik \((0, 0)\) dan \((1, 1)\)
Gradien garis \(g\) adalah \(m_{g} = \dfrac{y_2\:-\:y_1}{x_2 \:-\:x_2}\)
\(m_{g} = \dfrac{1\:-\:0}{1 \:-\:0} = 1\)
Persamaan garis melalui titik \((x_1, y_1)\) dan bergradien \(m\) adalah \(\color{blue} y\:-\:y_1 = m(x\:-\:x_1)\)
Persamaan garis melalui titik \((0, 0)\) dan bergradien \(m = 1\) adalah:
\(y\:-\:0 = 1(x\:-\:0)\)
\(y = x\)
Salah
garis \(g\) melalui titik \((0, 0)\) dan \((1, 1)\)
Gradien garis \(g\) adalah \(m_{g} = \dfrac{y_2\:-\:y_1}{x_2 \:-\:x_2}\)
\(m_{g} = \dfrac{1\:-\:0}{1 \:-\:0} = 1\)
Persamaan garis melalui titik \((x_1, y_1)\) dan bergradien \(m\) adalah \(\color{blue} y\:-\:y_1 = m(x\:-\:x_1)\)
Persamaan garis melalui titik \((0, 0)\) dan bergradien \(m = 1\) adalah:
\(y\:-\:0 = 1(x\:-\:0)\)
\(y = x\)
-
Pertanyaan 9 dari 20
9. Pertanyaan
1 points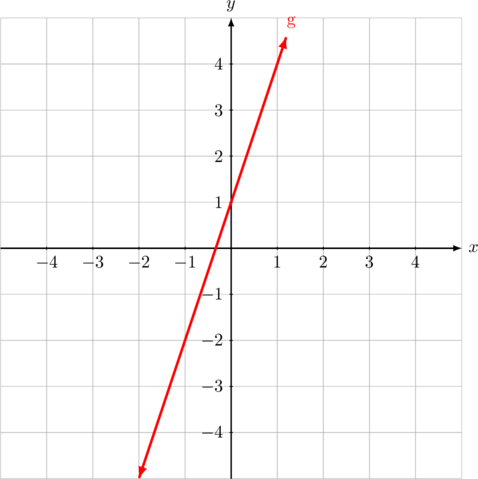
Persamaan garis \(g\) adalah…
Benar
garis \(g\) melalui titik \((0, 1)\) dan \((1, 4)\)
Gradien garis \(g\) adalah \(m_{g} = \dfrac{y_2\:-\:y_1}{x_2 \:-\:x_2}\)
\(m_{g} = \dfrac{4\:-\:1}{1 \:-\:0} = 3\)
Persamaan garis melalui titik \((x_1, y_1)\) dan bergradien \(m\) adalah \(\color{blue} y\:-\:y_1 = m(x\:-\:x_1)\)
Persamaan garis melalui titik \((0, 1)\) dan bergradien \(m = 3\) adalah:
\(y\:-\:1 = 3(x\:-\:0)\)
\(y = 3x + 1\)
Salah
garis \(g\) melalui titik \((0, 1)\) dan \((1, 4)\)
Gradien garis \(g\) adalah \(m_{g} = \dfrac{y_2\:-\:y_1}{x_2 \:-\:x_2}\)
\(m_{g} = \dfrac{4\:-\:1}{1 \:-\:0} = 3\)
Persamaan garis melalui titik \((x_1, y_1)\) dan bergradien \(m\) adalah \(\color{blue} y\:-\:y_1 = m(x\:-\:x_1)\)
Persamaan garis melalui titik \((0, 1)\) dan bergradien \(m = 3\) adalah:
\(y\:-\:1 = 3(x\:-\:0)\)
\(y = 3x + 1\)
-
Pertanyaan 10 dari 20
10. Pertanyaan
1 points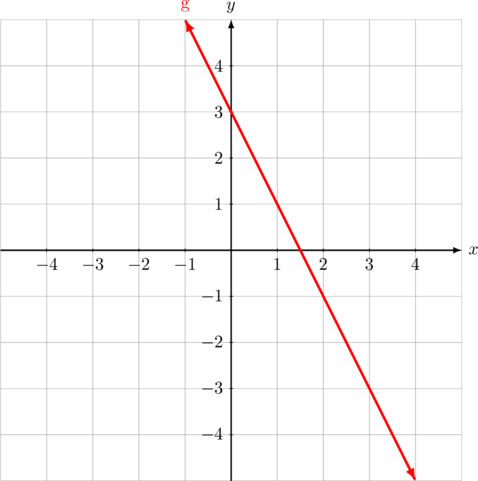
Persamaan garis \(g\) adalah…
Benar
garis \(g\) melalui titik \((0, 3)\) dan \((2, -1)\) (kalian juga bisa pilih titik yang lain asalkan dilalui oleh garis g)
Gradien garis \(g\) adalah \(m_{g} = \dfrac{y_2\:-\:y_1}{x_2 \:-\:x_2}\)
\(m_{g} = \dfrac{-1\:-\:3}{2 \:-\:0} = -2\)
Persamaan garis melalui titik \((x_1, y_1)\) dan bergradien \(m\) adalah \(\color{blue} y\:-\:y_1 = m(x\:-\:x_1)\)
Persamaan garis melalui titik \((0, 3)\) dan bergradien \(m = -2\) adalah:
\(y\:-\:3= -2(x\:-\:0)\)
\(y = -2x + 3\)
Salah
garis \(g\) melalui titik \((0, 3)\) dan \((2, -1)\) (kalian juga bisa pilih titik yang lain asalkan dilalui oleh garis g)
Gradien garis \(g\) adalah \(m_{g} = \dfrac{y_2\:-\:y_1}{x_2 \:-\:x_2}\)
\(m_{g} = \dfrac{-1\:-\:3}{2 \:-\:0} = -2\)
Persamaan garis melalui titik \((x_1, y_1)\) dan bergradien \(m\) adalah \(\color{blue} y\:-\:y_1 = m(x\:-\:x_1)\)
Persamaan garis melalui titik \((0, 3)\) dan bergradien \(m = -2\) adalah:
\(y\:-\:3= -2(x\:-\:0)\)
\(y = -2x + 3\)
-
Pertanyaan 11 dari 20
11. Pertanyaan
1 pointsPersamaan garis yang sejajar dengan garis \(10x + 5y + 7 = 0\) dan melalui titik \((-1, -2)\) adalah…
Benar
Langkah 1: Menentukan gradien garis \(10x + 5y + 7 = 0\). Namakan \(m_1\).
\(5y = -10x\:-\:7\)
Bagi kedua ruas dengan 5
\(y = \color{red} -2x \color{black} \:-\:\dfrac{7}{5}\)
\(m_1 = -2\)
Langkah 2: Menemukan gradien garis yang sejajar dengan \(10x + 5y + 7 = 0\). Namakan \(m_2\).
Syarat dua garis saling sejajar adalah \(m_1 = m_2\)
Jadi \(m_2 = -2\)
Langkah 3: Menentukan persamaan garis yang melalui titik \((-1, -2)\) dan bergradien \(m_2 = -2\)
Gunakan rumus \(\color{blue} y\:-\:y_1 = m(x\:-\:x_1)\)
\(y \:-\:(-2) = -2(x\:-\:(-1))\)
\(y + 2 = -2(x + 1)\)
\(y = -2x\:-\:2\:-\:2\)
\(y = -2x \:-\:4\)
\(2x + y + 4 = 0\)
Jadi, persamaan garis yang sejajar dengan garis \(10x + 5y + 7 = 0\) dan melalui titik \((-1, -2)\) adalah\(2x + y + 4 = 0\).
Salah
Langkah 1: Menentukan gradien garis \(10x + 5y + 7 = 0\). Namakan \(m_1\).
\(5y = -10x\:-\:7\)
Bagi kedua ruas dengan 5
\(y = \color{red} -2x \color{black} \:-\:\dfrac{7}{5}\)
\(m_1 = -2\)
Langkah 2: Menemukan gradien garis yang sejajar dengan \(10x + 5y + 7 = 0\). Namakan \(m_2\).
Syarat dua garis saling sejajar adalah \(m_1 = m_2\)
Jadi \(m_2 = -2\)
Langkah 3: Menentukan persamaan garis yang melalui titik \((-1, -2)\) dan bergradien \(m_2 = -2\)
Gunakan rumus \(\color{blue} y\:-\:y_1 = m(x\:-\:x_1)\)
\(y \:-\:(-2) = -2(x\:-\:(-1))\)
\(y + 2 = -2(x + 1)\)
\(y = -2x\:-\:2\:-\:2\)
\(y = -2x \:-\:4\)
\(2x + y + 4 = 0\)
Jadi, persamaan garis yang sejajar dengan garis \(10x + 5y + 7 = 0\) dan melalui titik \((-1, -2)\) adalah\(2x + y + 4 = 0\).
-
Pertanyaan 12 dari 20
12. Pertanyaan
1 pointsPersamaan garis yang tegak lurus dengan garis \(x\:-\:2y + 10 = 0\) dan melalui titik \((-6, 0)\) adalah…
Benar
Langkah 1: Menemukan gradien garis \(x\:-\:2y + 10 = 0\). Namakan \(m_1\).
\(-2y = -x\:-\:10\)
Bagi kedua ruas dengan \(-2\)
\(y =\color{red} \dfrac{1}{2} \color{black} x + 5\)
\(m_1 = \dfrac{1}{2}\)
Langkah 2: Menemukan gradien garis yang tegak lurus dengan \(x\:-\:2y + 10 = 0\). Namakan \(m_2\).
Syarat dua garis saling tegak lurus adalah \(m_1 \cdot m_2 = -1\)
\(\dfrac{1}{2} \cdot m_2 = -1\)
\(m_2 = -2\)
Langkah 3: Menentukan persamaan garis yang melalui titik \((-6, 0)\) dan bergradien \(m_2 = -2\).
Gunakan rumus \(\color{blue} y\:-\:y_1 = m(x\:-\:x_1)\)
\(y\:-\:0 = -2(x\:-\:(-6))\)
\(y = -2x \:-\:12\)
\(y + 2x + 12 = 0\)
Salah
Langkah 1: Menemukan gradien garis \(x\:-\:2y + 10 = 0\). Namakan \(m_1\).
\(-2y = -x\:-\:10\)
Bagi kedua ruas dengan \(-2\)
\(y =\color{red} \dfrac{1}{2} \color{black} x + 5\)
\(m_1 = \dfrac{1}{2}\)
Langkah 2: Menemukan gradien garis yang tegak lurus dengan \(x\:-\:2y + 10 = 0\). Namakan \(m_2\).
Syarat dua garis saling tegak lurus adalah \(m_1 \cdot m_2 = -1\)
\(\dfrac{1}{2} \cdot m_2 = -1\)
\(m_2 = -2\)
Langkah 3: Menentukan persamaan garis yang melalui titik \((-6, 0)\) dan bergradien \(m_2 = -2\).
Gunakan rumus \(\color{blue} y\:-\:y_1 = m(x\:-\:x_1)\)
\(y\:-\:0 = -2(x\:-\:(-6))\)
\(y = -2x \:-\:12\)
\(y + 2x + 12 = 0\)
-
Pertanyaan 13 dari 20
13. Pertanyaan
1 points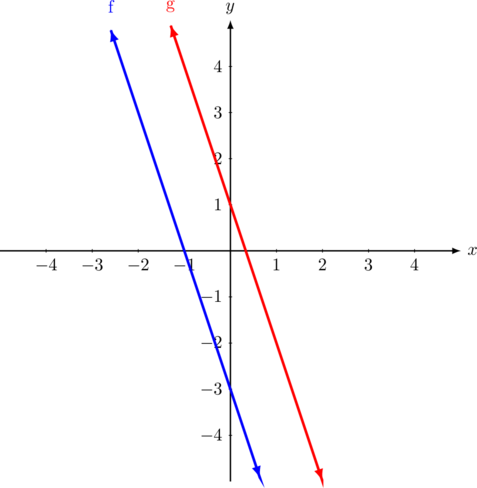
Diketahui:
Garis \(g\) sejajar dengan garis \(f\)
Garis \(g\) melalui titik \((-1, 4)\) dan \((0, 1)\).
Garis \(f\) melalui titik \((0, -3)\).
Persamaan garis \(f\) adalah…
Benar
Langkah 1: Menentukan gradien garis \(g\). Namakan \(m_1\)
Garis \(g\) melalui titik \((-1, 4)\) dan \((0, 1)\).
\(m_1= \dfrac{y_2\:-\:y_1}{x_2 \:-\:x_1}\)
\(m_1 = \dfrac{1\:-\:4}{0 \:-\:(-1)}\)
\(m_1= \dfrac{-3}{1}\)
\(m_1= -3\)
Langkah 2:Menentukan gradien garis \(f\). Namakan \(m_2\).
Garis \(g\) dan \(f\) saling sejajar, maka \(m_1 = m_2\)
\(m_2 = -3\)
Langkah 3: Menentukan persamaan garis \(f\).
Garis \(f\) melalui titik \((0, -3)\) dan bergradien \(-3\)
\(\color{blue} y\:-\:y_1 = m(x\:-\:x_1)\)
\(y\:-\:(-3) = -3(x\:-\:0)\)
\(y + 3= -3x\)
\(y = -3x\:-\:3\)
\(y + 3x + 3 = 0\)
Salah
Langkah 1: Menentukan gradien garis \(g\). Namakan \(m_1\)
Garis \(g\) melalui titik \((-1, 4)\) dan \((0, 1)\).
\(m_1= \dfrac{y_2\:-\:y_1}{x_2 \:-\:x_1}\)
\(m_1 = \dfrac{1\:-\:4}{0 \:-\:(-1)}\)
\(m_1= \dfrac{-3}{1}\)
\(m_1= -3\)
Langkah 2:Menentukan gradien garis \(f\). Namakan \(m_2\).
Garis \(g\) dan \(f\) saling sejajar, maka \(m_1 = m_2\)
\(m_2 = -3\)
Langkah 3: Menentukan persamaan garis \(f\).
Garis \(f\) melalui titik \((0, -3)\) dan bergradien \(-3\)
\(\color{blue} y\:-\:y_1 = m(x\:-\:x_1)\)
\(y\:-\:(-3) = -3(x\:-\:0)\)
\(y + 3= -3x\)
\(y = -3x\:-\:3\)
\(y + 3x + 3 = 0\)
-
Pertanyaan 14 dari 20
14. Pertanyaan
1 points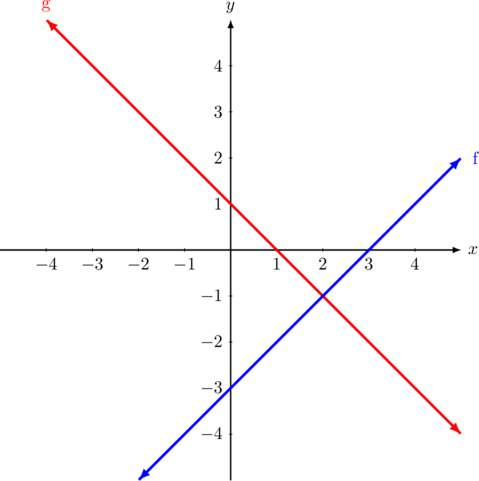
Diketahui:
Garis \(g\) melalui titik \((0, 1)\) dan \((-3, 4)\)
Garis \(f\) melalui titik \((3, 0)\)
Garis \(g\) dan \(f\) saling tegak lurus.
Persamaan garis \(f\) adalah…
Benar
Langkah 1: Menentukan gradien garis \(g\). Namakan \(m_1\)
Garis \(g\) melalui titik \((0, 1)\) dan \((-3, 4)\)
\(m_1= \dfrac{y_2\:-\:y_1}{x_2 \:-\:x_1}\)
\(m_1 = \dfrac{4\:-\:1}{-3\:-\:0}\)
\(m_1= \dfrac{3}{-3}\)
\(m_1= -1\)
Langkah 2:Menentukan gradien garis \(f\). Namakan \(m_2\).
Garis \(g\) dan \(f\) saling tegak lurus, maka \(m_1\cdot m_2 = -1\)
\(-1 \cdot m_2 = -1\)
\(m_2 = 1\)
Langkah 3: Menentukan persamaan garis \(f\).
Garis \(f\) melalui titik \((3, 0)\) dan bergradien \(1\)
\(\color{blue} y\:-\:y_1 = m(x\:-\:x_1)\)
\(y\:-\:0 = 1(x\:-\:3)\)
\(y = x\:-\:3\)
\(y \:-\:x + 3 = 0\)
Jadi, persamaan garis \(f\) adalah \(y \:-\:x + 3 = 0\)
Salah
Langkah 1: Menentukan gradien garis \(g\). Namakan \(m_1\)
Garis \(g\) melalui titik \((0, 1)\) dan \((-3, 4)\)
\(m_1= \dfrac{y_2\:-\:y_1}{x_2 \:-\:x_1}\)
\(m_1 = \dfrac{4\:-\:1}{-3\:-\:0}\)
\(m_1= \dfrac{3}{-3}\)
\(m_1= -1\)
Langkah 2:Menentukan gradien garis \(f\). Namakan \(m_2\).
Garis \(g\) dan \(f\) saling tegak lurus, maka \(m_1\cdot m_2 = -1\)
\(-1 \cdot m_2 = -1\)
\(m_2 = 1\)
Langkah 3: Menentukan persamaan garis \(f\).
Garis \(f\) melalui titik \((3, 0)\) dan bergradien \(1\)
\(\color{blue} y\:-\:y_1 = m(x\:-\:x_1)\)
\(y\:-\:0 = 1(x\:-\:3)\)
\(y = x\:-\:3\)
\(y \:-\:x + 3 = 0\)
Jadi, persamaan garis \(f\) adalah \(y \:-\:x + 3 = 0\)
-
Pertanyaan 15 dari 20
15. Pertanyaan
1 pointsGaris \(2y + ax + b = 0\) memiliki gradien \(-3\) dan melalui titik \((-1, 2)\). Nilai \(a + b = \dotso\)
Benar
\(2y + ax + b = 0\)
\(2y = -ax\:-\:b\)
Bagi kedua ruas dengan 2
\(y = -\dfrac{a}{2}x\:-\:\dfrac{b}{2}\)
Gradien garisnya adalah koefisien dari \(x\) yaitu \(-\dfrac{a}{2}\).
\(-\dfrac{a}{2} = -3\)
kali silang,
\(-a = -6\)
\(a = 6\)
Garis \(2y + ax + b = 0\) melalui titik \((-1, 2)\).
\(2y + 6x + b = 0\)
\(2(2) + 6(-1) + b = 0\)
\(4 \:-\:6 + b = 0\)
\(-2 + b = 0\)
\(b = 2\)
Jadi, nilai \(a + b = 6 + 2 = 8\)
Salah
\(2y + ax + b = 0\)
\(2y = -ax\:-\:b\)
Bagi kedua ruas dengan 2
\(y = -\dfrac{a}{2}x\:-\:\dfrac{b}{2}\)
Gradien garisnya adalah koefisien dari \(x\) yaitu \(-\dfrac{a}{2}\).
\(-\dfrac{a}{2} = -3\)
kali silang,
\(-a = -6\)
\(a = 6\)
Garis \(2y + ax + b = 0\) melalui titik \((-1, 2)\).
\(2y + 6x + b = 0\)
\(2(2) + 6(-1) + b = 0\)
\(4 \:-\:6 + b = 0\)
\(-2 + b = 0\)
\(b = 2\)
Jadi, nilai \(a + b = 6 + 2 = 8\)
-
Pertanyaan 16 dari 20
16. Pertanyaan
1 pointsTerdapat beberapa persamaan garis.
(1) \(x + 4y \:-\:2 = 0\)
(2) \(2x + y + 5 = 0\)
(3) \(3x + y + 6 = 0\)
(4) \(4x + 16y \:-\:1 = 0\)
Pasangan garis yang saling sejajar adalah…
Benar
Dua garis saling sejajar jika memiliki gradien yang sama \(\color{blue} m_1 = m_2\)
Garis 1
\(x + 4y \:-\:2 = 0\)
\(4y = -x + 2\)
\(y = -\dfrac{1}{4}x + \dfrac{2}{4}\)
Gradien garis 1 adalah \( -\dfrac{1}{4}\)
Garis 2
\(2x + y + 5 = 0\)
\(y = -2x \:-\:5\)
Gradien garis 2 adalah \(-2\)
Garis 3
\(3x + y + 6 = 0\)
\(y = -3x\:-\:6\)
Gradien garis 2 adalah \(-3\)
Garis 4
\(4x + 16y \:-\:1 = 0\)
\(16y = -4x + 1\)
\(y = – \dfrac{4}{16}x + \dfrac{1}{16}\)
\(y = -\dfrac{1}{4}x + \dfrac{1}{16}\)
Gradien garis 4 adalah \(-\dfrac{1}{4}\)
Jadi, pasangan garis yang saling sejajar adalah garis 1 dan garis 4 karena sama-sama memiliki gradien \(-\dfrac{1}{4}\).
Salah
Dua garis saling sejajar jika memiliki gradien yang sama \(\color{blue} m_1 = m_2\)
Garis 1
\(x + 4y \:-\:2 = 0\)
\(4y = -x + 2\)
\(y = -\dfrac{1}{4}x + \dfrac{2}{4}\)
Gradien garis 1 adalah \( -\dfrac{1}{4}\)
Garis 2
\(2x + y + 5 = 0\)
\(y = -2x \:-\:5\)
Gradien garis 2 adalah \(-2\)
Garis 3
\(3x + y + 6 = 0\)
\(y = -3x\:-\:6\)
Gradien garis 2 adalah \(-3\)
Garis 4
\(4x + 16y \:-\:1 = 0\)
\(16y = -4x + 1\)
\(y = – \dfrac{4}{16}x + \dfrac{1}{16}\)
\(y = -\dfrac{1}{4}x + \dfrac{1}{16}\)
Gradien garis 4 adalah \(-\dfrac{1}{4}\)
Jadi, pasangan garis yang saling sejajar adalah garis 1 dan garis 4 karena sama-sama memiliki gradien \(-\dfrac{1}{4}\).
-
Pertanyaan 17 dari 20
17. Pertanyaan
1 pointsTerdapat beberapa persamaan garis.
(1) \(2x \:-\: 2y \:-\:5 = 0\)
(2) \(x + y + 6 = 0\)
(3) \(-2x + y + 10 = 0\)
(4) \(-6x + 3y \:-\:1 = 0\)
Pasangan garis yang saling tegak lurus adalah…
Benar
Dua garis saling tegak lurus jika memenuhi \(\color{blue} m_1 \cdot m_2 = -1\)
Garis 1
\(2x \:-\: 2y \:-\:5 = 0\)
\(2y = 2x\:-\:5\)
\(y = x \:-\:\dfrac{5}{2}\)
Gradien garis 1 adalah \(1\).
Garis 2
\(x + y + 6 = 0\)
\(y = -x\:-\:6\)
Gradien garis 2 adalah \(-1\).
Garis 3
\(-2x + y + 10 = 0\)
\(y = 2x\:-\:10\)
Gradien garis 3 adalah \(2\).
Garis 4
\(-6x + 3y \:-\:1 = 0\)
\(3y = 6x + 1\)
\(y = 2x + \dfrac{1}{3}\)
Gradien garis 4 adalah \(2\)
Jadi, pasangan garis yang saling sejajar adalah garis 1 dan garis 2, karena memenuhi \(m_1 \cdot m_2 = -1\)
\(1 \cdot (-1) = -1\).
Salah
Dua garis saling tegak lurus jika memenuhi \(\color{blue} m_1 \cdot m_2 = -1\)
Garis 1
\(2x \:-\: 2y \:-\:5 = 0\)
\(2y = 2x\:-\:5\)
\(y = x \:-\:\dfrac{5}{2}\)
Gradien garis 1 adalah \(1\).
Garis 2
\(x + y + 6 = 0\)
\(y = -x\:-\:6\)
Gradien garis 2 adalah \(-1\).
Garis 3
\(-2x + y + 10 = 0\)
\(y = 2x\:-\:10\)
Gradien garis 3 adalah \(2\).
Garis 4
\(-6x + 3y \:-\:1 = 0\)
\(3y = 6x + 1\)
\(y = 2x + \dfrac{1}{3}\)
Gradien garis 4 adalah \(2\)
Jadi, pasangan garis yang saling sejajar adalah garis 1 dan garis 2, karena memenuhi \(m_1 \cdot m_2 = -1\)
\(1 \cdot (-1) = -1\).
-
Pertanyaan 18 dari 20
18. Pertanyaan
1 pointsGaris \(2x + 5y \:-\:10 = 0\) memotong sumbu X di titik \((m, 0)\) dan memotong sumbu Y di titik \((0, n)\). Nilai \(3m\:-\:2n = \dotso\)
Benar
Garis \(2x + 5y \:-\:10 = 0\) memotong sumbu X jika \(y = 0\)
\(2x + 5(0) \:-\:10 = 0\)
\(2x = 10\)
\(x = 5\)
Jadi titik potong garis terhadap sumbu X adalah \((5, 0)\) sehingga nilai \(m = 5\)
Garis \(2x + 5y \:-\:10 = 0\) memotong sumbu Y jika \(x = 0\)
\(2(0) + 5y\:-\:10 = 0\)
\(5y = 10\)
\(y= 2\)
Jadi titik potong garis terhadap sumbu Y adalah \((0, 2)\) sehingga nilai \(n = 2\)
Nilai \(3m\:-\:2n = 3(5)\:-\:2(2) = 15\:-\:4 = 11\).
Salah
Garis \(2x + 5y \:-\:10 = 0\) memotong sumbu X jika \(y = 0\)
\(2x + 5(0) \:-\:10 = 0\)
\(2x = 10\)
\(x = 5\)
Jadi titik potong garis terhadap sumbu X adalah \((5, 0)\) sehingga nilai \(m = 5\)
Garis \(2x + 5y \:-\:10 = 0\) memotong sumbu Y jika \(x = 0\)
\(2(0) + 5y\:-\:10 = 0\)
\(5y = 10\)
\(y= 2\)
Jadi titik potong garis terhadap sumbu Y adalah \((0, 2)\) sehingga nilai \(n = 2\)
Nilai \(3m\:-\:2n = 3(5)\:-\:2(2) = 15\:-\:4 = 11\).
-
Pertanyaan 19 dari 20
19. Pertanyaan
1 pointsGaris \(y = 2x\) akan memotong garis \(y = x\:-\:3\) di titik yang berabsis…
Benar
Untuk mencari absis (koordinat X) titik potong dua buah garis, substitusikan \(y = 2x\) ke dalam persamaan garis \(y = x\:-\:3\).
\(2x = x\:-\:3\)
\(2x\:-\:x = -3\)
\(x = -3\)
Jadi, absis titik potong kedua garis tersebut adalah \(-3\)
Salah
Untuk mencari absis (koordinat X) titik potong dua buah garis, substitusikan \(y = 2x\) ke dalam persamaan garis \(y = x\:-\:3\).
\(2x = x\:-\:3\)
\(2x\:-\:x = -3\)
\(x = -3\)
Jadi, absis titik potong kedua garis tersebut adalah \(-3\)
-
Pertanyaan 20 dari 20
20. Pertanyaan
1 pointsGaris \(y = mx + 5\) dan garis \(x + 2y \:-\:4 = 0\) berpotongan di titik yang berabsis 2. Nilai \(m\) yang memenuhi adalah…
Benar
Substitusikan \(y = mx + 5\) ke dalam persamaan garis \(x + 2y \:-\:4 = 0\).
\(x + 2(mx + 5)\:-\:4 = 0\)
\(x + 2mx + 10 \:-\:4 = 0\)
\(x + 2mx + 6 = 0\)
Karena kedua garis berpotongan di titik yang berabsis 2, maka gantilah \(x\) dengan 2.
\(2 + 2m(2) + 6 = 0\)
\(8 + 4m = 0\)
\(4m = -8\)
\(m = – \dfrac{8}{4}\)
\(m = -2\)
Jadi, nilai \(m\) yang memenuhi adalah \(-2\).
Salah
Substitusikan \(y = mx + 5\) ke dalam persamaan garis \(x + 2y \:-\:4 = 0\).
\(x + 2(mx + 5)\:-\:4 = 0\)
\(x + 2mx + 10 \:-\:4 = 0\)
\(x + 2mx + 6 = 0\)
Karena kedua garis berpotongan di titik yang berabsis 2, maka gantilah \(x\) dengan 2.
\(2 + 2m(2) + 6 = 0\)
\(8 + 4m = 0\)
\(4m = -8\)
\(m = – \dfrac{8}{4}\)
\(m = -2\)
Jadi, nilai \(m\) yang memenuhi adalah \(-2\).
