Lingkaran pertama \(\textbf{L}_1\) dan lingkaran kedua \(\textbf{L}_2\) saling berpotongan secara tegak lurus apabila garis singgung pada lingkaran pertama berimpit dengan jari-jari pada lingkaran kedua dan garis singgung pada lingkaran kedua berimpit dengan jari-jari pada lingkaran pertama.
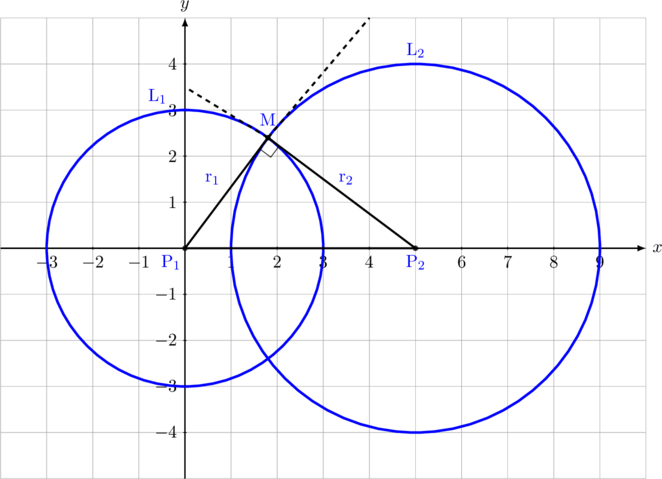
Perhatikan segitiga siku-siku yang terbentuk,
Lingkaran pertama \(\textbf{L}_1\) berpotongan secara tegak lurus dengan lingkaran kedua \(\textbf{L}_2\) jika memenuhi:
Jika lingkaran \(x^2 + y^2 = 9\) berpotongan tegak lurus dengan lingkaran \(x^2 + y^2 \:-\:10x + m = 0\) maka tentukan nilai \(m\) yang memenuhi.
\(\textbf{L}_1 : x^2 + y^2 = 3^2\)
Pusat:
\(\text{P}_1 = (0, 0)\)
Jari-jari:
\(r_1 = 3\)
\(\textbf{L}_2 : x^2 + y^2 \:-\:10x + m = 0\)
Pusat:
\(\text{P}_2 = [-\frac{1}{2}(-10), -\frac{1}{2}(0)]\)
\(\text{P}_2= (5, 0)\)
Jari-jari:
\(r_2 = \sqrt{5^2 + (0)^2\:-\:m}\)
\(r_2 = \sqrt{25\:-\:m}\)
Kuadrat jarak antara kedua pusat lingkaran \((\text{P}_1\text{P}_2)^2\) adalah:
\((\text{P}_1\text{P}_2)^2 = (x_2\:-\:x_1)^2 + (y_2\:-\:y_1)^2\)
\((\text{P}_1\text{P}_2)^2 = (5\:-\:0)^2 + (0\:-\:0)^2\)
\((\text{P}_1\text{P}_2)^2 = 25\)
\( r^2_1 + r^2_2 = (\text{P}_1\text{P}_2)^2\)
\(3^2 + (\sqrt{25\:-\:m})^2 = 25\)
\(9 + 25 \:-\:m = 25\)
\(m = 9\)
Jadi nilai \(m\) yang memenuhi adalah 9
